मुझे डर लगता है गणित से

गंगा गुप्ता

हमारी गणित की पूरी क्षमता स्मृति पर टिकी रहती है। याद की गई विधियां भूलने पर गणित से खौफ खाना स्वाभाविक है, है न!

गणित का नाम सुनते ही पता नहीं क्यों मेरे हाथ-पैर फूलने लगते हैं। वैसे कक्षा की दृष्टि से मैं कभी भी गणित विषय में कमजोर नहीं रही हूं। मेरे सवाल हमेशा ही कक्षा में सबसे पहले हो जाया करते थे। हमेशा मुझे शाबाशी मिलती। सब साथी मेरी नकल करके उत्तर लिखते थे और गुरुजी को दिखाने से पहले उत्तर मुझसे मिला लेते थे। अब जाने क्या हो गया है वे सवाल जो फटाफट निकलते थे, अब मुझसे नहीं बनते। मैं अक्सर सोचती हूं कि ऐसा क्यों है।

इसका एक कारण तो मुझे यह लगता है कि उस समय मुझे वो प्रक्रिया याद थी।शायद समझ नहीं आई थी पर उसके सारे स्टेप (कदम) यांत्रिक रूप से मैं कर सकती थी। सवाल मिला नहीं कि धड़ाधड़ एक के बाद एक स्टेप कर दिए और उत्तर निकाल दिया। और फिर सवाल करने के उस तरीके को समझना इसलिए भी नहीं कहा जा सकता क्योंकि दो-चार महीने के बाद यदि उसकी एकाध स्टेप भी भूल जाओ तो फिर पूरा सवाल ही नहीं बनता। आठवीं बोर्ड में मुझे गणित में 79% अंक मिले। तब गणित के अंक देखकर मुझे सभी ने कहा कि तुम्हें गणित विषय लेना चाहिए। परन्तु मेरे अंदर आत्मविश्वास की कमी ने ही मुझे पीछे धकेल दिया। अब हालत यह है कि आठवीं तक भी मैंने जो कुछ सीखा था

जब मैं छोटी थी तो इस बात से उलझी रहती थी कि दस और एक ग्यारह या एक पर एक ग्यारह पढ़ाते हैं, इसका अर्थ क्या होता है।

वह भी काफी गड्डमड्ड हो गया है। वैसे भी वो कभी साफ था ही नहीं और उसकी मूल बातें तो मेरी समझ में कभी नहीं आईं। वैसे जब मैं छोटी थी तो इस बात से बहुत उलझी रहती थी कि दस और एक ग्यारह या एक पर एक ग्यारह पढ़ाते हैं, इसका मतलब क्या होता है।

स्कूल की नौकरी मिलने के बाद पढ़ाना शुरू कर दिया। वहां पर साथियों से इन सवालों के बारे में पूछा तो भी कुछ स्पष्ट उत्तर नहीं मिला। कुल मिलाकर बात समझ नहीं आई। फिर 1987 में एकलव्य के प्राथमिक शिक्षा में नवाचार' के काम से जुड़ी। जब इस कार्यक्रम में स्थानीय मान की मूल अवधारणा के बारे में चर्चा हुई तब कुछ-कुछ स्पष्टता मिली। साथ ही जब मैंने बच्चों को इकाई, दहाई समझाने की कोशिश की तब ठीक से ख्याल आया कि इकाई, दहाई और स्थानीय मान में क्या संबंध है।

मुझे अभी तक गुणज और गुणनखंड में भ्रम होता है। गुणज यानी क्या और गुणनखंड यानी क्या? जब हम कहते हैं कि 15 के गुणनखंड हैं 3 और 5 - तो इसमें 15 गुणज है का क्या मतलब? और 3 व 5 गुणनखंड कैसे हो गए? पर मैं गुणनखंड फटाफट निकाल लेती थी और अभी भी निकाल सकती हैं। इस सबको मैं बार-बार समझने की कोशिश करती हूं। पर बार-बार समझने पर भी कोई फायदा नहीं होता है। यदि कोई अचानक गुणज पूछ ले तो अभी भी अटपटा जाती हूं। इसी प्रकार लघुत्तम-महत्तम निकालने का यांत्रिक तरीकाः

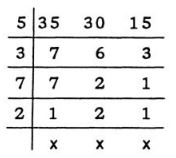
5 x 3 x 7 x 2 = 230

अब ये क्या होता है, और इससे क्या पता चलता है?

मुझे मालूम नहीं कि इस तरह की चीजें पांचवीं कक्षा तक या आगे क्यों आवश्यक हैं? मुझे तो आज तक समझ नहीं आता कि इसकी मूल अवधारणा क्या है? इसे मैंने अलग-अलग लोगों से समझने की भी कोशिश की है पर बहुत प्रयत्न करने पर भी समझ में नहीं आता| एक मानसिक जड़ता है इसके बारे में सोचने में, जैसे कोई दीवार खड़ी हो जिसे तोड़ा न जा सके और न ही उसके पार जाया जा सके।

इसी प्रकार साधारण जोड़-घटाना के मौखिक सवाल तो थोड़े-बहुत बन जाते हैं पर वे भी जल्दी और पूरे आत्मविश्वास के साथ नहीं। सारे पहाड़े जो मुझे याद थे जाने अब कहां चले गए? सच, सोच कर शर्म आती है कि मुझे गणित में विशेष योग्यता मिलती थी। अगर अभी भी कहा जाए कि 2 को 3 बार और 3 को 3 बार प्रयोग करके (यानि +, -, X और घात की क्रियाएं उपयोग करके) 24 लाओ तो काफी दिमाग लगाने पर भी मुझसे नहीं बनता| आठवीं में समीकरण के सवाल (पिता की आयु x है तो पुत्र की क्या होगी) मैं बहुत ही आसानी से कर लेती थी। और तब मज़ा भी आता था। मेरे शिक्षक भी बहुत खुश होते थे। पर अब उसका एक भी स्टेप पता नहीं है। मुझे लगता है कि गणित में जब तक मुझे प्रक्रिया याद थी तब तक तो करने में मज़ा आता था पर एकाध स्टेप भूलने पर कुछ समझ नहीं आता। अभ्यास छूटने के साथ-साथ ये सब भूलता जाता है और एक-दूसरे में गड्डमड्ड होता जाता है। यानी गुणज का स्टेप वर्गमूल में घुसा और वर्गमूल का गुणनखंड में। वैसे भ्रम में डालने के लिए और गड्डमड्ड होने के लिए और भी बहुत सारे कलन हैं, जिनमें बहुत सारे स्टेप होते हैं।

चूंकि न तो गुणनखंड की समझ है और न ही वर्गमूल की और न उस प्रक्रिया की जिससे इन्हें निकाला जाता है तो बस गणित की पूरी क्षमता याददाश्त पर टिकी रहती है।

इसी प्रकार भिन्न के जोड़-घटाना, गुणा, भाग के सवाल भी हैं। मैं दावे से कह सकती हूं कि भिन्न के जोड़, घटा, बड़ी-छोटी संख्याएं ढूंढने, क्रम में जमाने के सवाल जो लोग कर पाते हैं। उनमें से 50% से भी ज्यादा केवल यांत्रिक ढंग से सूत्रों का उपयोग करके हल करते हैं उन्हें। न वे खुद समझते हैं कि वे क्या कर रहे हैं और जाहिर है कि न वे समझा सकते हैं कि सवाल कैसे हल किया या हल करने का तरीका कैसे समझा जा सकता है।

3/5+2/3

9+10/15=19/15

या 9/15 और 10/15 निकाल कर पता करना कि 2/3 बड़ी है।

अब इसमें 9/15 कैसे आ गया? 9/15 और 3/5 में क्या संबंध है? लघुत्तम क्यों निकाला? ये सब उन्हें कुछ समझ नहीं आता। बस सवाल मिला और फट से हल कर दिया। और मेरी तरह कहीं भूल गए, तो बैठे हैं कि अब क्या करें? मैंने इसे बहुत समझने की कोशिश की पर किसी ने समझाया ही नहीं। सबकी कोशिश यही थी कि किसी तरह सवाल हल करने का तरीका याद कर लें (उनके शब्दों में सीख जाऊँ)। कलनों को व तरीकों को समझने की तो कोई प्रथा ही नहीं है।

जब मैं पढ़ाने लगी और हमारी नवाचार की किताबों व पाठ्यक्रम में छात्रों से समझने की अपेक्षा दिखने लगी तो मैं घबराई।जो मुझे समझ नहीं आता, वो सब बच्चों को कैसे समझाऊं! कलन तो उन्हें याद करवा दूं, किताब में दिए सब सवाल हल करवा दूं, रटवा दूं - पर समझाऊं कैसे? और हम शिक्षकों ने ही तो तय किया था कि इस नए कार्यक्रम में छात्रों के मूल्यांकन में किताब का कोई प्रश्न नहीं होगा अब नई इबारत, नई संख्याओं के सवाल हल करने के लिए तो प्रक्रिया व प्रश्न की समझ चाहिए। वह समझ कहां से आए?

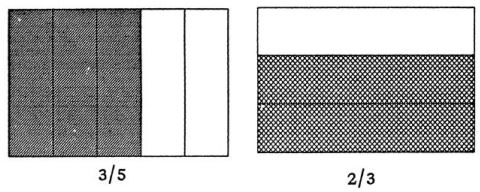इतने साल बाद अब मुझे भिन्न की अवधारणा चित्रों के माध्यम से समझ में आने लगी है। इसलिए अब ये भिन्न के सवाल वास्तव में खेल जैसे लगने लगे और मैंने कक्षा में पूरे आत्मविश्वास के साथ बच्चों के साथ उन्हें किया।और बच्चे भी इन्हें आसानी से कर पाते हैं। - जैसे यदि 3/5 और 2/3 में मुझे बड़ी भिन्न, छोटी भिन्न समझना है तो सबसे पहले मैंने उन दोनों भिन्न संख्याओं के चित्र बनाए

पहले चित्र में कुल 5 भाग हैं और दूसरे में कुल 3 भाग। जब इन दोनों को इकट्ठा करके एक ही चित्र में बनाया तो हमारे पास कुल 15 भाग हो गए।

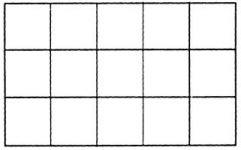अब इन 15 भागों में से हमने पहले चित्र के भाग उसे दे दिए। ऐसे ही दूसरे चित्र को भी उसके भाग दे दिए।

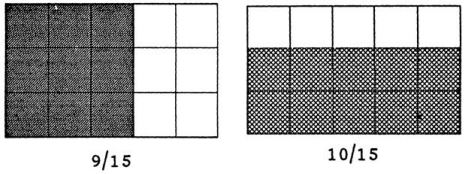इन चित्रों को देखते ही समझ में आ जाता है। कि 9/15 और 10/15 कहां से आए।

अब आसानी से बता सकते हैं कि जिसके खाने ज्यादा रंगे वो भिन्न बड़ा है। यानी 10/15 या 2/3 बड़ा है। और जोड़ के लिए भी हम उसके दोनों कुल रंगे भाग आसानी से जोड़ सकते हैं। अब मुझे लगता है कि पहले भिन्न की अवधारणा समझ कर, बाद में उसके यांत्रिक स्टेप (कदम) सीखें तो शायद वो उतना डरावना नहीं लगेगा। ऐसे ही गणित के अन्य पहलुओं को भी समझने की ज़रूरत होगी।

पर सवाल सिर्फ प्राथमिक शिक्षा या जोड़, गुणा, भाग, भिन्न पर थोड़े ही रुकता है। मैंने अर्थशास्त्र में एम.ए. किया है, और बी.ए. प्रथम वर्ष से एम.ए.अंतिम वर्ष तक हमेशा सांख्यिकी के सवाल ठीक करके आई हूं। पर अभी मुझसे कोई पूछे किं मध्यक या प्रमाण विचलन क्या है? इसे कैसे निकालते हैं? क्या किया था? कुछ भी मालूम नहीं। यह सवाल तो भूल ही जाओ कि इसे क्यों निकालते हैं। और इसका क्या उपयोग है? मुझे रेखागणित में भी केवल आकृतियां बनाना और उनके नाम देना व उनसे खेलना अच्छा लगता है। पर त्रिज्या, परिधि, शंकु, बेलन आदि के बारे में ऊटपटांग सवाल करना, उनके सूत्र याद करना, बिल्कुल अच्छा नहीं लगता। प्रमेय में अ, ब, स को लेकर क्या करना है? क्यों अ ब स लेते हैं? क्या सिद्ध करना है? क्यों करना है? कुछ पता नहीं चलता। फिर सिद्ध करने के लिए ये अ, ब, स से पता नहीं क्या-क्या करना होता है। बहुत बुरा लगता है। आठवीं में मुझे याद है कि कैसे हमने महत्वपूर्ण प्रमेयों को रट-रटकर समझा था और परीक्षा में ज्यों का त्यों आने पर कितने खुश हुए थे। मेरे साथ एक बात शायद अच्छी हुई है कि मेरी खुद की गणित में विशेष समझ और ज्ञान न होने से, मेरे स्कूल के बच्चे गणित में अच्छे रहे हैं। और मुझसे ज्यादा आगे कर पाए हैं, क्योंकि गणित सीखने में जो दिक्कत या कठिनाई आती है उसका अहसास होने के कारण मैंने बच्चों की दिक्कतों को समझा। सीधे सही उत्तर की अपेक्षा नहीं की। जिससे शायद उन्हें और मुझे सीखने में मदद मिली। मेरे स्कूल के कुछ बच्चे तो बहुत-सी नई बातें खुद करने लगे हैं और कई बार तो मैं पांचवीं के बच्चों से समझती हूं कि इस में क्या-क्या करना है। जैसे मैंने लिखा कि 2, 3 और +, -, X का प्रयोग करके 18 बनाओ। मेरे कुछ बच्चे आसानी से ढूंढ लेते हैं। इतना ही नहीं इस प्रकार की कुछ और भी संख्याएं लेकर वे नए-नए सवाल बनाते हैं और मुझे भी सिखाते हैं!

ऐसा कैसे हो कि गणित थोड़ा समय अच्छा लगने की बजाए हमेशा अच्छा लगे और जो सवाल, जो बातें सीखते समय या परीक्षा के समय ही याद रहती हैं और हल की जा सकती हैं, वे सब पांच साल बाद भी अच्छी लगें। जब तक मुझे यह समझ नहीं आएगा, मालूम नहीं होगा स्वाभाविक है कि मैं गणित से भागती रहूंगी व डरती रहूंगी।

(गंगा गुप्ता प्राथमिक शाला, पाठई, जिला बैतूल में पढ़ाती हैं। प्राथमिक शिक्षा के नवाचार कार्यक्रमों में सक्रिय।)

समझदार बगुले

गाय-भैंस की पीठ पर बैठकर कौओं को छोटे-छोटे कीड़ों-मकोड़ों को खाते हुए आपने अक्सर देखा होगा। जानवरों की त्वचा पर ही नहीं घास में भी असंख्य छोटे-छोटे कीड़े-मकोड़े छिपे होते हैं जो सरसरी तौर पर आंखों से दिखाई नहीं देते और अपने दुश्मनों की नजरों से बचे रहते हैं। लेकिन ये कीड़े-मकोड़े कभी-न-कभी तो नजर आएंगे ही न?

अब देखिए एक हाथी आराम से चला जा रहा है और पीछे-पीछे बगुले दावत उड़ाते हुए चले जा रहे हैं। बुबुलकस-एबिस नामक बगुलों ने इस बात को अच्छी तरह से समझ लिया है कि हाथी घास पर जहां-जहां भारी-भरकम कदम रखेगा वहां घास के हिलने पर कीड़े-मकोड़े इधर-उधर भागते हैं। तो देर किस बात की? हाथी के पीछे-पीछे चलते रहो और शानदार दावत का इंतजाम पक्का!