हम वैसे ही पढ़ाते हैं, जैसा हमें पढ़ाया गया था

--शेषगिरी केएम राव

“औसत शिक्षक बताता है। अच्छा शिक्षक समझाता है। श्रेष्ठ शिक्षक करके बताता है। महान शिक्षक प्रेरित करता है।”
- विलियम आर्थर वार्ड

सितम्बर 1993 - दी वैली स्कूल में मैं प्रिंसिपल के कमरे में उनके सामने बैठा हूँ। मैं एक शिक्षक बनना चाहता हूँ और अपना जीवन बच्चों के साथ बिताना चाहता हूँ। कुछ है जो मुझे बताता है कि तब मेरा जीवन ज़्यादा सार्थक होगा। मैं अपनी दो साल पुरानी नौकरी छोड़ना चाहता हूँ, जहाँ मेरा काम था सम्पन्न किसानों के लिए ट्रैक्टर निर्माण, जिनसे मैं कभी नहीं मिला हूँ।

जी हाँ, मैंने बारहवीं के बाद मेकेनिकल इंजीनियरिंग का कोर्स किया था, लेकिन वह तो साथियों के दबाव और परिवार की अपेक्षाओं के कारण था। अब मैं चाहता हूँ कि बदलाव हो। मैं हमारी बेमज़ा शिक्षा व्यवस्था से नाराज़ हूँ जो हमें मशीनी ढंग से सीखने को धकेलती है। मैं अपने अन्दर आदर्शवाद का उफान महसूस कर रहा हूँ और शिक्षक बनकर दुनिया को बदलना चाहता हूँ।

तब मेरा मानना था, और आज भी है, कि शिक्षा वास्तव में एक दूसरी दुनिया को मुमकिन बनाने का शुरुआती बिन्दु है। लिहाज़ा, मैंने तकरीबन 20 स्कूलों के बारे में पता किया और फिर इस वाले में आ पहुँचा। उन 20 स्कूलों ने मुझसे बी.एड. या एम.एड. की उपाधि की माँग की थी। कहाँ से लाता मैं? उस समय मुझे नहीं लगा था कि मुझे इनकी ज़रूरत है। मैं तो पढ़ाने के विचार को टटोल रहा था और मुझे लग रहा था कि मैं एक अच्छा शिक्षक बनूँगा।

जिस ट्रैक्टर निर्माण कम्पनी में मैं काम करता था, वहाँ मेरे बॉस ने अपना फैसला सुना दिया था कि मैं पलायनवादी हूँ, यानी कि मैं ज़िन्दगी से भाग रहा हूँ। जब मैं उन्हें समझाने उनके कमरे में गया कि मैं क्यों कुछ और करना चाहता हूँ तो उन्होंने बहुत अनमने ढंग से सिर हिलाते हुए कहा था, “तुम अभी बहुत छोटे हो और समझ नहीं पाओगे कि तुम क्या कर रहे हो।” उन्होंने मुझे खारिज कर दिया था। उस समय मेरे पास कोई जवाब नहीं था यानी ज़िन्दगी से पलायन करने के उनके इस ताने का कोई मुँहतोड़ जवाब नहीं था। क्या मैं सचमुच पलायनवादी हूँ? यह सवाल बार-बार मेरे सामने आता रहा।

स्कूल शिक्षक बनने के कुछ महीने बाद, मैं ज़्यादा आत्मविश्वास से उनके पास गया और कहा, “मैं ज़िन्दगी से भाग नहीं रहा हूँ, भागकर ज़िन्दगी में जा रहा हूँ, और ऐसा करके मैं ज़्यादा खुश हूँ।” उन्हें फिर भी समझ नहीं आया कि मैं एक स्कूल में शिक्षक क्यों बना हूँ। मुझे परवाह नहीं थी कि उन्हें समझ नहीं आया। मैंने निर्णय कर लिया था और इस नई यात्रा को लेकर उत्साहित था। अपने दिल की बात जो सुन रहा था मैं।

जब मैं शिक्षक बना
जिन प्रिंसिपल की मेज़ के दूसरी ओर मैं बैठा था, उन्होंने नम्रता-से मगर थोड़ा झिझक के साथ कहा, “हमें एक गणित शिक्षक की तलाश है। हम तुम्हें दो महीने देखेंगे और फिर फैसला करेंगे...अव्वल तो बच्चे तुम्हें पसन्द करें।” मैंने राहत की साँस ली कि किसी ने बी.एड. या एम.एड. का सार्टिफिकेट नहीं माँगा।
दो महीने बाद उन्हें मुझे नौकरी देने में कोई दिक्कत नहीं थी। मेरा ख्याल है, मैं ठीक-ठाक शिक्षक था। अपने शिक्षण को लेकर मेरी यही छवि है।

अच्छी बात यह थी कि कोई मेरी कक्षाओं की निगरानी नहीं करता रहता था। मुझसे हर हफ्ते पाठ योजना प्रस्तुत करने को नहीं कहा जाता था, जैसा कि कई निजी स्कूलों में शिक्षकों को करना होता है। स्कूल प्रबन्धन को हम पर भरोसा था। यह दार्शनिक व शिक्षक जिड्डू कृष्णमूर्ति के आदर्शों से प्रेरित एक प्रगतिशील स्कूल था। लिहाज़ा, हम शिक्षकों को प्रयोग करने के लिए ज़्यादा गुंजाइश थी।
मैं मुख्यत: मिडिल व हाई स्कूल में गणित और भौतिकी पढ़ाता था। थोड़े समय के लिए मैंने प्रायमरी कक्षाओं को भी पढ़ाया  था। यह एकदम नया अनुभव था और मैंने बहुत कुछ सीखा। हर क्षण जीवित होने का एहसास मिलता था। सब कुछ बहुत ताज़गी भरने वाला था। मुझे समझ में आया कि शिक्षण खुद को शिक्षित करने का बढ़िया तरीका है। हम खुद के बारे में और जिस दुनिया में हम रहते हैं, उसके बारे में दिलचस्प और बुनियादी सवाल पूछा करते थे। इन सवालों ने हमें एक भरपूर जीवन जीने में समर्थ बनाया।

चन्ना से प्रेरणा लेकर मैंने वे तमाम तकनीकें आज़माईं जिनका इस्तेमाल वे एक शिक्षक के नाते किया करते थे - जैसे बुनियादी बातें पढ़ाना, छात्रों को सोचने को विवश करना। और फिर उन्हें धकेलना और ठेलना, लेकिन पका-पकाया ज्ञान कभी न परोसना। और उन्हें गणित के इतिहास की दिलकश और पेचीदा कहानियाँ सुनाना। कक्षा में इस इतिहास की बात करना मैं कभी नहीं भूलता था। वैली स्कूल के पुस्तकालय ने मुझे अच्छी किताबें उपलब्ध कराईं और मैंने खूब पढ़ीं। साथी शिक्षकों के साथ भी रोचक वार्तालाप हुआ करते थे।

जब भी सम्भव होता, मैं छात्रों को ऐतिहासिक पगडण्डियों पर ले जाता। हमने पायथागोरस प्रमेय, त्रिकोणमिति, विश्लेषणात्मक ज्यामिति, लॉगरिद्म से सम्बन्धित प्राचीन सवाल हल किए, और गणित में विरोधाभासों पर खूब चर्चा की। इनमें से कई चर्चाओं को मैंने अपनी वर्कशीट्स में शामिल किया था और प्रश्न पत्र बनाते समय उन पर आधारित सवाल देने की भी कोशिश करता था। ब्लैकबोर्ड को शिक्षण की सहायक सामग्री के तौर पर इस्तेमाल करते हुए मैं जो कुछ भी करता था, वह मैंने चन्ना को देख-देखकर सीखा था। मेरी कोशिश होती थी कि ब्लैकबोर्ड का उपयोग अच्छे से और साफ-सुथरे ढंग से करूँ।

और तो और, मैंने ‘वैदिक गणित’ में भी चहलकदमी की थी, उसकी कुछ शॉर्टकट विधियों का प्रदर्शन करके बच्चों को उसके प्रति उत्साहित भी किया था, और साथी शिक्षकों के साथ इस बात पर बहसें भी की थीं कि एक गणित प्रणाली के रूप में यह (वैदिक गणित) कितना प्रामाणिक है। क्या इसका उद्गम सचमुच वेदों में है, जैसा कि कुछ लोग दावा करते हैं? मुझे याद है, मैं स्थानीय आर.एस.एस. शाखा द्वारा बैंगलुरु में चामराजपेट में आयोजित वैदिक गणित की एक कार्यशाला में भी शरीक हुआ था। हम त्रिघात समीकरण (cubic equations) छुड़ाने की कोशिश कर रहे थे और ‘जादुई शॉर्टकट’ पूरे शबाब पर थे। श्रोता कई बार वाह-वाह कर उठे थे। किन्तु जब मैंने स्रोत व्यक्ति से कहा कि वे बोर्ड पर उनके द्वारा लिखी गई त्रिघात समीकरण में ‘X’ का गुणांक बदल दें, तो वैदिक विधि गड़बड़ा गई। इससे इस दावे पर सवाल उठ खड़ा हुआ कि यह गणित वेदों से है। बहरहाल, मेरे छात्र मेरे द्वारा सिखाई गई हर बात को लपक लेते थे, बशर्ते कि वह काम करे।

थोड़ा भटकाव तो होगा, किन्तु मुझे यह बताना चाहिए कि वैदिक गणित को लेकर यह चर्चा एक ज़्यादा व्यापक सवाल की द्योतक है। सवाल का सम्बन्ध सत्य की तलाश और शिक्षा के लिए उसके निहितार्थ से है। मैंने प्रमाण सम्बन्धी अध्याय में संक्षेप में इसका इशारा किया था। वहाँ मैंने कहा था कि गणितीय प्रमाण एक विशिष्ट सन्दर्भ (निर्देश तंत्र या फ्रेम ऑफ रेफरेंस) में किसी दावे की सत्यता स्थापित करने का प्रयास होता है।

जैसा कि हमने देखा है, गणित का अध्ययन हमें गणितीय सत्यों (जैसे प्रमेयों) की समझ हासिल करने में मदद करता है। किन्तु गणित प्रकृति के सत्यों को उजागर करने का एक बढ़िया औज़ार भी है। ऐसा क्यों है, हम नहीं जानते। गणितीय तर्क और विचार शैली की ताकत गणित को यह समझने का भी एक अपरिहार्य औज़ार बना देती है कि समाज कैसे काम करता है। मैं यह सब पहले भी कह चुका हूँ, इसलिए आगे बढ़ने की इजाज़त दीजिए।

मैं अमरीकी दार्शनिक और शिक्षा विचारक नील पोस्टमैन की बात दोहराना चाहूँगा। उन्होंने कहा था कि शिक्षा का उद्देश्य ‘बकवास की शिनाख्त’ होना चाहिए। मेरा मत है कि गणित सीखने से हमें बकवास की शिनाख्त में बहुत मदद मिल सकती है और यह हमें एक सच्चे प्रजातांत्रिक समाज की ओर ले जा सकता है। शायद कह सकते हैं कि यही गणित की सामाजिक भूमिका है।
वह ‘बकवास’ क्या है, जिसकी शिनाख्त की जानी है? अधिकार-सम्पन्न लोग अपने सबसे प्रिय विश्वासों का प्रचार-प्रसार करने के लिए अक्सर धार्मिक, सांस्कृतिक, राजनैतिक और पहचान-आधारित तर्कों का इस्तेमाल करते हैं। वे अपनी ताकत और अन्य लोगों पर नियंत्रण को बरकरार रखने के लिए गलतफहमियों, गलत मान्यताओं, अन्धविश्वासों और यहाँ तक कि झूठ को सच बताने तक का सहारा लेते हैं। पाठ्यक्रम और पाठ्यपुस्तकें इन ‘सत्यों’ को पूरे समाज में फैलाने के आसान तरीके हैं। हमारी शिक्षा का इतिहास ऐसे उदाहरणों से भरा पड़ा है। आजकल सोशल मीडिया संचार का एक शक्तिशाली हथियार बन गया है। बढ़ते क्रम में, हमसे अपेक्षा की जा रही है कि हम भावनाओं और आस्थाओं का सहारा लें, भले ही तथ्य इन आस्थाओं को झुठला रहे हों। जिस ‘बकवास’ की बात मैं कर रहा हूँ, वह यही है, जिसे शिक्षा और खासकर गणित शिक्षा के माध्यम से उजागर किया जाना चाहिए। क्यों इसे चुपचाप झेलें?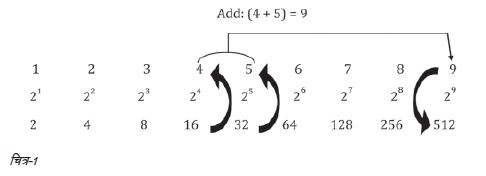

हमारे ज़माने के आवेशित माहौल में आलोचनात्मक खोजबीन और असहमति के स्वरों को राजद्रोह की संज्ञा दी जाती है। यदि मैं सार्वजनिक रूप से वैदिक गणित पर या हमारी पहचान, अतीत और संस्कृति को लेकर किए जा रहे अन्य सन्दिग्ध दावों पर सवाल उठाऊँ तो शायद मुझे कड़ी निन्दा से नवाज़ा जाएगा। ये सारे दावे हमारी विरासत की महानता स्थापित करने के लिए तैनात किए जाते हैं। तो मेरा तर्क है कि आलोचनात्मक खोजबीन की संस्कृति, गणित सीखना जिसका अभिन्न अंग है, बच्चों को ‘बकवास’ को पहचानने में मददगार हो सकती है।

कुछ गणित शिक्षण के अनुभव
शिक्षक के रूप में अपने अनुभव पर लौटता हूँ। वैली स्कूल में मेरे छात्रों और मैंने कई ‘आहा!’ क्षणों का लुत्फ लिया। मुझे याद है कि जब मैंने कक्षा-9 के छात्रों को एक छोटी-सी तालिका (चित्र-1) की मदद से बताया था कि लॉगरिद्म का जुगाड़ काम कैसे करता है, कैसे वह गुणा और भाग की जटिल संक्रियाओं को जोड़ और बाकी की सरल संक्रियाओं में तबदील कर देता है, तो वे अवाक रह गए थे। यह विचार लॉगरिद्म के मूल में है, जो हम छात्रों को कभी नहीं बताते।

पहली पंक्ति की संख्याएँ एक ‘अंकगणितीय श्रृंखला की सदस्य हैं  (जिसमें हम प्राकृतिक संख्याओं की सूची भर बनाते हैं) और सबसे निचली पंक्ति की संख्याएँ जिस श्रृंखला का अंग हैं उसे ‘ज्यामितीय श्रृंखला कहते हैं (जिसमें हर संख्या पिछली संख्या को दुगना करके मिलती है)। जैसा कि आप देख ही सकते हैं, बीच की पंक्ति की संख्याएँ, निचली पंक्ति की संख्याओं को 2 के आधार पर परिवर्तित करके बनी हैं। जैसे 16 को लिखा गया है 2⁴ और 32 को 2⁵ लिखा गया है। यहाँ 2 को आधार कहते हैं जबकि 4 और 5 घातांक कहलाते हैं। हम अन्य आधारों का भी उपयोग कर सकते हैं किन्तु बात को आगे बढ़ाने के लिए यही उदाहरण लेकर चलते हैं।

मान लीजिए हमें 16 में 32 का गुणा (16 x 32) करना है। आप 16 और 32 से सम्बन्धित संख्याओं (यानी क्रमश: 4 और 5) को पहली पंक्ति में देखेंगे। इन्हें जोड़ दीजिए: 4 + 5 = 9. निचली पंक्ति में 9 से सम्बन्धित संख्या क्या है? यह है 512. तो यह रहा आपका उत्तर! अद्भुत है, नहीं? जब कक्षा 9 के छात्र इसे समझ गए तो वे लगभग अविश्वास से बोल उठे, “ऐसा है?” मैंने जवाब दिया, “बिलकुल, लॉगरिद् म की अवधारणा इसी तरह काम करती है।” यहाँ गुणा को वास्तव में एक जोड़ की तरह किया जाता है, जिसके चलते वह सिर्फ सरल ही नहीं त्वरित भी हो जाता है। ऐसा ही तर्क भाग के मामले में भी काम करता है, जिसे घटाने के रूप में किया जाता है। क्या आप 256/8 को उपरोक्त तालिका की मदद से हल कर सकते हैं?

यह लॉगरिद्म की कक्षा तो है नहीं, इसलिए मैं इसके बारे में और चर्चा नहीं करूँगा; मुझे यकीन है कि इसे लेकर आपके कई सवाल हैं। उदाहरण के लिए 20 x 17 कैसे करेंगे? या उससे भी रोचक सवाल होगा कि 3.2  x 5.4 कैसे किया जाएगा? वगैरह। जब चीज़ें जटिल होने लगती हैं, तब क्या होता है? आप तमाम किस्म के भाग के सवालों के बारे में भी पूछ सकते हैं। और 2 की बजाय आप अन्य संख्याओं को आधार बना सकते हैं। मैंने जो तर्क पेश किया है, वह नहीं बदलता। अलबत्ता, कुछ और बातें कहना मुनासिब है।

उन लॉगरिद्म तालिकाओं को याद कीजिए जिनका इस्तेमाल हमने सवाल हल करने में किया था, जिनमें तमाम संख्याएँ बारीक अक्षरों में लिखी होती हैं। वे सब चित्र-1 में दर्शाए गए तर्क के आधार पर बनाई गई हैं। पहली पंक्ति में लॉगरिद्म होते हैं, अर्थात् वह घातांक जो आधार ‘a’ पर लगाने से निर्धारित संख्या मिलेगी। 16 x 32 के हमारे उदाहरण में 16 को लीजिए। 16 प्राप्त करने के लिए आधार 2 पर क्या घातांक लगाना होगा? जवाब है 4 क्योंकि 24 = 16 होता है। इसी प्रकार से 32 के लिए घातांक 5 है क्योंकि 25 = 32. इसे हम आम तौर पर इस तरह लिखते हैं: log₂16 = 4 और log₂32 = 5.
यहाँ 4 और 5 (घातांक) को लॉगरिद्म कहते हैं। यानी जब हम किसी संख्या के आगे ‘log’ लिखते हैं, तो इसका मतलब होता है: घातांक पता करें। तब हम एक आसान-सा नियम लागू करते हैं:

a^m x aⁿ = a^m+n

वर्तमान उदाहरण में 2⁴ x 2⁵ = 2⁴⁺⁵ = 2⁹

तो लॉगरिद्म हमें लॉग्स को जोड़ने में मदद करते हैं: log₂16 + log₂32 = 4 + 5 = 9 और इस तरह से गुणा को एक आसान जोड़ के सवाल में बदल देते हैं। किन्तु यह तो ज़ाहिर है कि जवाब 9 नहीं है। इसलिए हमें एक बार फिर अपनी तालिका को देखना पड़ेगा कि निचली पंक्ति (जिन्हें एंटी-लॉगरिद्म कहते हैं) में कौन-सी संख्या लॉगरिद्म पंक्ति के 9 से मेल खाती है। आप तालिका में देख ही सकते हैं कि जवाब है 512.

लॉगरिद्म का बुनियादी सिद्धान्त (और लॉगरिद्म तालिका) महान यूनानी गणितज्ञ आर्किमिडीज़ को ईसा पूर्व तीसरी सदी में ज्ञात था। लेकिन इसकी बारीकियों का विवरण करने का काम पूरी एक सहस्त्राब्दि उपरान्त सत्रहवीं सदी में स्कॉटिश गणितज्ञ जॉन नेपियर ने किया। दुनिया भर में व्यापार और नौवहन में विस्तार के साथ कठिन संख्याओं की गणनाएँ करने की ज़रूरतें भी बढ़ गई थीं और ये विवरण व्यावहारिक रूप से ज़रूरी हो गए थे। लॉगरिद्म ने राहत प्रदान की। फर्मा के समान नेपियर भी गणित में शौकिया तौर पर जुड़े थे।

ज्ञान का निर्माण काफी श्रमसाध्य काम है। इसलिए बच्चों को ज्ञान की समझ बनाने में मदद के कदम काफी सोच-समझकर तय किए जाने चाहिए। जब उन्हें इस श्रमसाध्य काम में अर्थ नज़र आने लगता है, तो उन्हें कोई नहीं रोक सकता।
मैंने अपने छात्रों को लॉगरिद्म की कहानी दो सत्रों में सुनाई थी। कल्पना कीजिए कि यदि इसकी बजाय मैं शुरुआत यहाँ से करता: “यदि a^x = y है, तो x को a के आधार पर y लॉगरिद्म कहते हैं।” आप झुंझलाकर बाल नहीं नोंच लेते? यही कारण है कि बच्चे गणित से कन्नी काटते हैं।

***

मुझे याद नहीं पड़ता कि चन्ना ने अपरिमेय π के बारे में इससे ज़्यादा चर्चा की थी कि वह एक अन्तहीन दशमलव संख्या है। लेकिन एक शिक्षक के रूप में मैंने इस पगली संख्या का खुलासा करने में काफी समय व्यतीत किया था। प्रसंगवश बता दूँ कि इस संख्या के नाम पर एक दिवस है - πदिवस हर वर्ष मार्च 14 को मनाया जाता है (क्या आप अन्दाज़ लगा सकते हैं कि मार्च 14 ही क्यों?)। हमने π को समझने के लिए एक गतिविधि की थी जो मैं आपके साथ साझा करना चाहूँगा। छात्रों को इसमें बहुत मज़ा आया था।
स्कूल विज्ञान दिवस पर हमने एक π दुम बनाई थी। मेरे पास π का कंप्यूटर-जनित मान 2500 दशमलव स्थानों तक था। यह मैंने पुस्तकालय की एक किताब से फोटोकॉपी किया था। विचार यह था कि इन सब दशमलव अंकों को एक दुम के रूप में लिखें और पूरे स्कूल को इस दुम से घेर दें। इसके लिए हमने अखबारों से 4 इंच चौड़ी पट्टियाँ बनाकर जोड़ लीं और उस (लम्बी-सी पट्टी) पर मार्कर पेन से सारे दशमलव अंक लिख दिए। छात्रों के पास जब भी फुरसत होती, वे गणित कक्ष में आकर पट्टी पर दशमलव अंक लिखते। इस काम को करने के लिए कई बार तो उन्होंने तड़ी भी मारी।
विज्ञान दिवस के दिन हमने यह लम्बी पट्टी (लगभग 850 फीट की) निकाली और पुस्तकालय के सामने लगे सूचना पटल से शुरू करके शब्दश: पूरे स्कूल को इस मनमौजी संख्या की अपरिमेय जकड़ में लपेट दिया।

हर किसी को कौतूहल था, खासकर छोटे बच्चों को। वे इस बेतुकी दुम के इर्द-गिर्द भाग रहे थे। स्कूल भवन के आसपास लहराते, कक्षाओं के अन्दर-बाहर, खिड़कियों में से बाहर निकलते, यहाँ तक कि शौचालयों में भी प्रवेश करते और अन्तत: ऊपर जाकर जंगल-जिम के पेड़ पर लिपटे हुए अन्तहीन अंकों से हैरान होकर वे इधर-से-उधर भाग रहे थे। जब मेरे कुछ छात्रों ने आकर कहा कि “अब हमें समझ आ गया है कि π को अपरिमेय संख्या क्यों कहते हैं... यह तो लगता है चलती ही जा रही है!” मैं समझ गया कि π दुम का असर हुआ है। ‘अनुभव-आधारित सीखने’ के बारे में यही कह सकते हैं। वैसे मैं पक्का नहीं कह सकता कि उन्होंने फिर कभी π के बारे में सोचा।

π से पंगा लेने का एक और मौका मुझे अँग्रेज़ी की कक्षा में हाथ लगा था। π के जितने चाहें दशमलव स्थान याद रखने के लिए आप स्मृति-युक्तियों (mnemonics) का इस्तेमाल कर सकते हैं। लेकिन यदि आप इस रहस्यमयी संख्या को फतह करना चाहते हैं तो इससे कोई बहुत बड़ी राहत नहीं मिलेगी।
एक बार मुझे एक गणित शिक्षक के तौर पर अँग्रेज़ी सृजनात्मक लेखन की कक्षा में बुलाया गया था। मैंने इस निमंत्रण को स्कूल में विषयों के बीच सेतु बाँधने के एक अवसर के रूप में लिया। मैंने π के प्रथम 100 दशमलव अंक लिखे और बच्चों से कहा कि एक पैराग्राफ लिखें जिसमें हर शब्द में उतने ही अक्षर हों जितना कि उस स्थान के अंक का मान है। उदाहरण के लिए 500 के प्रथम सात अंकों (3.1415926) को इस तरह लिखा जा सकता है: “May (3) I (1) have (4) a (1) large (5) container (9) of (2) coffee (6)?” इस नियम का पालन करते हुए छात्रों ने कुछ ऐसी मज़ेदार चीज़ें लिखीं कि अगले कई दिनों तक हम लोट-पोट होते रहे। बदकिस्मती से मैंने उनके लेखन के नमूने इकट्ठे नहीं किए थे।
आप देख ही सकते हैं, जब मैं शिक्षक बना तो चन्ना की विरासत मेरे अन्दर काफी सशक्त रूप से जीवित रही। एक अच्छा गणित शिक्षक आप में ऐसे परिवर्तन ला सकता है।

गणित इतिहास के आइने में
1994 में वैली स्कूल में एक महत्वपूर्ण घटना हुई जिसने गणित के विकास के इतिहास की मेरी समझ में आमूल परिवर्तन कर दिया। मैंने कुछ नया सीखा और चन्ना ने हमें जहाँ छोड़ा था, वहाँ से आगे बढ़ गया। मेरे एक वरिष्ठ सहकर्मी थे जिनकी रुचि भी यह समझने में थी कि विभिन्न संस्कृतियों में सहस्त्राब्दियों में गणित का विकास कैसे हुआ। उन्हें पता चला कि मैनचेस्टर विश्वविद्यालय के गणित के एक विद्वान जॉर्ज गेवर्गीस जोसेफ शहर में आए हुए हैं। जोसेफ ने गणित की ‘गैर-यूरोपीय जड़ों’ पर व्यापक अनुसन्धान किया था।

उन्हें अपने स्कूल में एक व्याख्यान देने को आमंत्रित करने के मकसद से हम जाकर उनसे मिले। हमारी खुशी का ठिकाना नहीं रहा जब उन्होंने फौरन हामी भर दी। जोसेफ का व्याख्यान आकर्षक था और परास बहुत व्यापक था। उन्होंने हमें बताया कि गणित और विज्ञान का पूरा कारोबार कैसे ‘युरो-केन्द्रित’ रहा है। दरअसल, आज तक हमें स्कूलों में बताया जाता है कि प्राचीन समय से ही यूरोप गणित और विज्ञान का वैश्विक केन्द्र था। ऐसा संकीर्ण नज़रिया इस तथ्य को अनदेखा कर देता है कि अन्य प्राचीन संस्कृतियों ने भी गणित व विज्ञान के विकास में काफी योगदान दिया है और कई मामलों में तो यह यूरोप में हुई खोजों से सैकड़ों वर्ष आगे था। खास तौर से अन्धकार युग में तो यूरोप महाद्वीप गहरी तन्द्रा में था।

जोसेफ ने इस नई समझ के सन्दर्भ में अपने प्रिय शोध प्रोजेक्ट के बारे में बताया - केरल गणित घराने की खोज। केरल गणित घराना अर्थात् केरल स्कूल ऑफ मैथेमेटिक्स चौदहवीं से सोलहवीं सदी के बीच संगमग्राम के माधव और तिरुर के नीलकण्ठ जैसे गणितज्ञों के काम के फलस्वरूप फला फूला था।
गणित के वैकल्पिक इतिहास पर अनुसंधान ने स्पष्ट रूप से दर्शा दिया है कि केरल घराना गणित के उस महान औज़ार - ‘केल्कुलस’ - की खोज से कम-से-कम 2 शताब्दी पूर्व अस्तित्व में था।  आम तौर पर न्यूटन और लीबनिट्ज़ को केल्कुलस के संस्थापक माना जाता है और उन्हें इस बात का श्रेय दिया जाना चाहिए कि उन्होंने विभिन्न अलग-अलग विचारों को केल्कुलस के सुसंगत धागे में पिरोया था, लेकिन साथ ही भारतीय, चीनी और अरब गणितज्ञों की खोजों को अनदेखा नहीं किया जा सकता।

जैसा कि जोसेफ ने बताया, हम इस बात को नज़रअन्दाज़ नहीं कर सकते कि मिस्र, बेबीलोन, चीन और भारत से गणितीय विचार अरब दुनिया के माध्यम से यूरोप तक पहुँचे थे। इस क्षेत्र में किए गए अनुसन्धानों ने इस बाबत अकाट्य प्रमाण प्रस्तुत किए हैं कि इस गणितीय संचार ने पायथागोरस के समय से ही यूरोपीय गणित के विकास को प्रभावित किया था। पायथागोरस को पता था कि मिस्र के गणितज्ञ उसका प्रमेय जानते थे और यह भी पता था कि उन्होंने इसको सिद्ध नहीं किया है। शायद उन्हें इसकी ज़रूरत भी नहीं थी क्योंकि उनका पूरा ज़ोर तो गणित के व्यावहारिक उपयोगों पर था।

जोसेफ से यह अचानक मुलाकात 1990 के मध्य दशक में हुई थी जब मैं एक शिक्षक था। इसकी बदौलत मैं उस कौतूहल को और टटोल सका जिसके बीज चन्ना ने 1980 के दशक में बोए थे। मैंने इन रोमांचक खोजों की बात अपने छात्रों से भी की। मैंने जोसेफ की पुस्तक क्रेस्ट ऑफ दी पीकॉक भी खरीद ली जिसमें उन्होंने यूरोप के बाहर किए गए गणित और खोजों की विस्तृत चर्चा की है। पुस्तक की शुरुआत मध्य भूमध्यरैखीय अफ्रीका से मिली ‘इशांगो अस्थि’ (Ishango bone) के गणित से होती है। इशांगो अस्थि का सम्बन्ध चन्द्र कैलेंडर से है। इससे साबित होता है कि गणित कम-से-कम 20,000 वर्ष पूर्व अस्तित्व में था। यह पुस्तक अत्यन्त पठनीय है और यकीनन आपकी आँखें खोल देगी।

मैं नहीं जानता कि दुनिया में गणित के विकास के इन वैकल्पिक दृष्टिकोणों को लेकर चन्ना का मत क्या है। वैसे भी हमने स्कूल में इसकी चर्चा नहीं की थी। आम तौर पर इतिहास पेचीदा, रोचक और फिसलनभरा होता है। गणित का इतिहास उससे अलग नहीं है।
जिन शख्सों ने मुझे ग्यारहवीं और बारहवीं में तथा इंजीनियरंग के चार वर्षों में पढ़ाया था, वे निसन्देह समर्पित शिक्षक थे। लेकिन वे सिर्फ परीक्षा को ध्यान में रखकर पढ़ाने के प्रति समर्पित थे। कोई कहानी नहीं, कोई परिप्रेक्ष्य नहीं, कल्पना की कोई उड़ान नहीं। महज़ सिलेबस पूरा करने के लिए गणित का शिक्षण। ऊपर से उन्होंने यह चेतावनी भी दे दी थी, “यदि तुम्हें फलाँ-फलाँ प्रतिशत अंक नहीं मिले तो तुम इंजीनियरिंग या मेडिसिन में प्रवेश नहीं कर पाओगे।”

गोया यही दो ठीक-ठाक करने योग्य काम थे।
ज्ञान अर्जित करने का आनन्द अनुभव करना एक बात है। लेकिन यह सवाल भी है कि आप उस ज्ञान का करते क्या हैं। कुछ समय तक मैंने खगोल शास्त्री या सैद्धान्तिक भौतिक शास्त्री बनने के सपने देखे क्योंकि मुझे लगता था कि भौतिकी एक ‘गहरा’ विज्ञान है। प्राकृतिक विश्व के बारे में ज्ञान के सृजन और खोज के प्रति जीवन समर्पित करना काफी लुभावना विचार था, लेकिन सामाजिक पहलू बार-बार लौटकर मेरे सामने आ जाता था। मैंने निर्णय किया कि वह ज्ञान सबके लिए सुलभ करना कहीं ज़्यादा उपयोगी काम होगा। ज्ञान का उद्घाटन कहीं अधिक महत्वपूर्ण कार्य है जिस पर तत्काल ध्यान देने की ज़रूरत है।
रोमांचक यात्रा वैली स्कूल के आगे भी जारी रही। रहना ही थी क्योंकि कारण कहीं अधिक गहरे थे।
...जारी

शेषागिरी केएम राव: यूनीसेफ, छत्तीसगढ़ में शिक्षा विशेषज्ञ हैं। प्रारम्भिक शिक्षा और बाल्यावस्था में विकास में विशेष रुचि। साथ ही, आधुनिक शैक्षिक मुद्दों पर लिखने में दिलचस्पी।
अँग्रेज़ी से अनुवाद: सुशील जोशी: एकलव्य द्वारा संचालित स्रोत फीचर सेवा से जुड़े हैं। विज्ञान शिक्षण व लेखन में गहरी रुचि।
यह लेख एकलव्य द्वारा प्रकाशित पुस्तक द मैन हू टॉट इंफिनिटी से लिया गया एक अंश है।
यह किताब एकलव्य, पिटारा में उपलब्ध है।