गणित और भौतिक जगत का सम्बन्ध

--दीपक धर

इस लेख में मैं गणित के भौतिक जगत, विज्ञान तथा मानवीय ज्ञान के अन्य क्षेत्रों से सम्बन्ध पर चर्चा करूँगा। मेरा मत है कि सारा गणित मनुष्य जाति द्वारा ही बनाया गया है, और गणित की मूलभूत अवधारणाओं और निर्मितियों जैसे ‘π’ अंक का अब से एक लाख वर्ष पूर्व कोई अस्तित्व ही नहीं था ।
“प्रकृति की किताब गणित की भाषा में लिखी गई है और इसके अक्षर त्रिकोण, वृत्त और अन्य ज्यामितीय आकृतियाँ हैं। इनके बिना इस पुस्तक का एक भी शब्द समझना असम्भव है और इनके बिना व्यक्ति एक अँधेरी भूलभुलैया में व्यर्थ भटकता है।”

गैलीलियो गैलिली,
(1623 ई. में प्रकाशित पुस्तक ‘इल साजियाटोरे’ में)

गणित और विज्ञान के बीच क्या सम्बन्ध है? इस प्रश्न पर दर्शनशास्त्रियों ने बहुत सोचा और लिखा है। इनके बारे में मैंने पहले अपनी किशोरावस्था में पढ़ा था। तब शायद मैं आसानी-से बहकाया जा सकता था। मैंने जो पढ़ा, उसे बिना पर्याप्त सोचे ही सच मान लिया। परन्तु पिछले कुछ वर्षों में, इस विषय पर और विचार करने के बाद, कई बातें जो उस समय बिलकुल सही लगती थीं, अब गलत लगती हैं। इस लेख के द्वारा मैं अपना यह नवार्जित ज्ञान पाठकों से बाँटना चाहता हूँ। यहाँ प्रस्तुत यह दृष्टिकोण और विचारधारा केवल मेरी अपनी सोच का परिणाम नहीं है। कई लोगों ने कई बार इससे पहले इसकी चर्चा की है। मैं यहाँ पर इन्हें सिर्फ दोहरा रहा हूँ क्योंकि ये अभी भी प्रचलित मान्यता के विरुद्ध हैं।

वैज्ञानिक लोग अक्सर दार्शनिक विषयों पर बहस से दूर रहना पसन्द करते हैं, और युवा शोधकर्ताओं को भी यही सलाह दी जाती है। कह सकते हैं कि दार्शनिक विषय पर बहस को कुछ अशिष्ट व्यवहार माना जाता है, या फिर बढ़ती उम्र का द्योतक। मुझे लगता है कि दर्शन शास्त्र की इस बदनामी का कारण है इस प्रकार की चर्चाओं की अपारदर्शिता। इस सम्बन्ध में डुबिस्लाव1 की एक उक्ति बहुत सटीक है, “दर्शनशास्त्र कुछ खास तौर पर बनाए गए शब्दों का दुरुपयोग है, और इन शब्दों को इसी काम के लिए बनाया जाता है।”

दार्शनिक विषयों से दूर रहने के विषय में मैं कहूँगा कि अधिकांश लोग इस बात से तो सहमत होंगे कि हमारे जीवन के अधिक महत्वपूर्ण प्रश्न तथाकथित दार्शनिक प्रश्न होते हैं। हमें युवा पीढ़ी को ऐसी सलाह नहीं देनी चाहिए, सिर्फ इसलिए कि इस प्रकार के प्रश्नों का सिर्फ एक और सर्वसम्मत उत्तर नहीं होता है, या इसलिए कि इस पर कोई नया रिसर्च पेपर नहीं लिखा जा सकता। यह भी ज़रूरी नहीं है कि दार्शनिक विषयों की चर्चा हमेशा दुरूह और अबोधगम्य ही हो। यहाँ मैं अपनी बात को सरल सुगम भाषा में कहने का प्रयास करूँगा। युवावर्ग में दार्शनिक मुद्दों पर चर्चा उनको अपने आप सोचने को प्रेरित करती है, उनकी विवेकशक्ति को बढ़ाती है और शायद उनकी कुछ गलतफहमियों को दूर कर सकती है। यह मेरी आशा है।

एक बात और। अक्सर, दार्शनिक विषयों के पाठकों के कुछ विश्वास और मान्यताएँ होती हैं । यदि लेखक जो कहता है, वह इनसे मिलता है, तो पाठक सोचता है, “ठीक है, ठीक है, ठीक है।” लेकिन यदि, लेखक कुछ और कहता है जो पाठक की सोच से फर्क है, तो पाठक अपने विचारों के पूर्वाग्रह से, बिना कुछ और सोचे, लेखक की बात को खारिज कर देता है। बिना यह देखे कि क्या उनका पूर्वाग्रह उचित है, या नहीं, और लेखक की दलील में कुछ ताकत है या नहीं। आशा है कि आप ऐसा नहीं करेंगे।

जन सामान्य का गणित के बारे में नज़रिया
कई लोगों के लिए गणित के प्रति भाव मुख्यतः डर या अरुचि का होता है और कुछ और लोगों के लिए मुख्य भाव विस्मय, आदर और घोर श्रद्धा का होता है। पहले नज़रिए के लिए आप किसी भी स्कूल के 10-20 छात्रों से पूछताछ कर लें। उनमें से करीब आधे तो सहमत होंगे। दूसरे नज़रिए का उदाहरण वेदांग ज्योतिष का यह श्लोक है:

“यथा शिखा मयूराणां, नागानां मणयो यथा।
तद्वद् वेदांगशास्त्राणां गणितं मूर्धनि स्थितम्॥”

अर्थात्, जैसे मोरों की कलगी और नागों में मणि की स्थिति सबसे ऊपर मूर्धा पर है, वैसे ही वेदांग शास्त्रों में गणित का स्थान है। कुछ लोग मानते हैं कि ईश्वर एक गणितज्ञ है, या शायद वह एक गणितज्ञ के आदेश पर काम करता है। महान जर्मन गणितज्ञ गाउस का मत था कि गणित विज्ञान के विषयों की साम्राज्ञी है|

वेदांग से लिए गए श्लोक से हमें लगेगा कि यह हमारे पूर्वज ऋषियों के संचित ज्ञान का सार है जो हमें विरासत में मिला है और गणित के बारे में ऐसी सोच शायद उस समय की सर्वसम्मत मान्यता थी। फिर भी, हम यह पूछ सकते हैं कि प्राचीन या मध्यकालीन भारत में, किसी भी एक समय पर, कितने लोगों को गणितज्ञ कहा जा सकता था। यहाँ हम किसी ऐसे व्यक्ति या महिला को गणितज्ञ कहेंगे जो न केवल भास्कराचार्य या माधव का नाम जानता/जानती हो, बल्कि उनके काम से भी परिचित हो, और इसे किसी छात्र को समझा सके, चाहे उसने अपने आप गणित पर कोई ग्रन्थ न लिखा हो। यह संख्या 5 के आसपास होगी, या 50 के आसपास, या फिर 500 के आसपास? इस विषय पर हमारे इतिहास के जानकार लोगों के अनुसार, यह संख्या 5 के निकट होने की सम्भावना अधिक है, न कि 50 के निकट। अतः, हमें यह मानना पड़ेगा कि यद्यपि वेदांग में उपरोक्त श्लोक जैसा कुछ कहा गया है और भारतीय गणितज्ञों की कई बड़ी जानी-मानी और प्रसिद्ध उपलब्धियाँ हैं, भारतीय दर्शन परम्परा में व्यवहारिक रूप में गणित को इतना ऊँचा दर्जा नहीं दिया गया। गाउस का कथन शायद उनके विचारों को ठीक ही व्यक्त करता है, पर उसे निष्पक्ष तो नहीं कहा जा सकता। इस लेख में हम गणित के मानवीय ज्ञान के अन्य क्षेत्रों के साथ सम्बन्ध पर नारेबाज़ी और पूर्वाग्रह से मुक्त एक नज़र डालना चाहते हैं।

चलिए, हम अपनी बात इस प्रश्न से शुरू करते हैं: क्या गणित के अंक π का अब से एक लाख वर्ष पूर्व कोई अस्तित्व था? मेरा अनुमान है कि अधिकांश पाठक सोच रहे हैं, “हाँ, बेशक।” यहाँ पर मैं यह कहना चाहूँगा कि यह मामला इतना साफ नहीं है, यदि आप इस विषय पर कुछ देर सोचने के बाद उत्तर दें।

पहले तो यह समझना ज़रूरी है कि यहाँ ‘अस्तित्व’ शब्द का क्या अर्थ है। यह तो स्पष्ट है कि अंक π कोई भौतिक वस्तु, जैसे मेज़ या बृहस्पति ग्रह, नहीं है। अतः, अंक π का अस्तित्व उसी अर्थ में तो नहीं हो सकता है जिस अर्थ में मेज़ का अस्तित्व है। भौतिक वस्तुओं का कुछ द्रव्यमान होता है, और वे कुछ समय के लिए अन्तरिक्ष में कुछ सुनिश्चित स्थान घेरती हैं । अंक π एक मानसिक निर्मिति (मेंटल कन्सट्रक्ट) है और इसका अस्तित्व केवल एक मानसिक निर्मिति जैसा हो सकता है ।

उदाहरण के तौर पर, मैं किसी आठ सर वाले ज़ेब्रा की बात करूँ। इस तरह का कोई पशु जगत में कहीं नहीं है। पर, इन शब्दों को एक साथ लाकर मैंने एक मानसिक निर्मिति बना ली, और अब विचारों के संसार में इस विचार का अस्तित्व शुरू हो जाता है। अब इस तरह के ज़ेब्राओं के कुछ गुण-धर्म हम स्थापित कर सकते हैं। जैसे, अगर हम पूछें कि ऐसे आठ सर वाले ज़ेब्रा की कितनी आँखें होती हैं? तो उत्तर है कि सोलह क्योंकि हर एक सर पर दो आँखें हैं।

जो बात आठ सर वाले ज़ेब्रा के सम्बन्ध में सच है, वही बात युक्लिडीय ज्यामिति की संरचनाओं, जैसे त्रुटिहीन वृत्त (perfect circle) पर भी लागू होती हैं। भौतिक जगत में कहीं भी कोई त्रुटिहीन वृत्त नहीं मिलेगा। पर त्रुटिहीन वृत्त के सम्बन्ध में अनेक प्रमेय इसकी परिभाषा का प्रयोग करके ही स्थापित किए जा सकते हैं, जैसा कि ज्यामिति की पाठ्यपुस्तकों में किया जाता है।
सन् 1960 ईसवी में भौतिक विज्ञानी विगनेर ने एक लेख लिखा था जिसका शीर्षक था ‘प्राकृतिक विज्ञान में गणित की अनपेक्षित उपयोगिता।4 यह लेख विज्ञान सम्बन्धी दार्शनिक प्रश्नों के विचारकों के बीच बहुत विचार-विमर्श और चर्चा का विषय बना। विगनेर द्वारा प्रस्तुत विचारों का विस्तृत विश्लेषण किया गया, और उन पर अनेक टिप्पणियाँ लिखी गईं। इनमें से एक थी हैमिंग की टिप्पणी, और उनकी बात को आगे बढ़ाकर एडिलेड विश्वविद्यालय में प्रोफेसर डैरेक एबट ने एक लेख लिखा, जिसका शीर्षक था ‘गणित की अपेक्षित अनुपयोगिता’|5 इस लेख को पढ़ने पर मुझे एबट की दलीलें सही लगीं और अपने नज़रिए को बदलना पड़ा। इस लेख के माध्यम से, मैं इस बदले नज़रिए का प्रचार करना चाहता हूँ।

विगनेर का दृष्टिकोण
पहले मैं विगनेर की विचारधारा को संक्षेप में बताता हूँ। विगनेर अपना लेख दो मित्रों की एक कहानी से शुरू करते हैं जो हाई स्कूल में सहपाठी थे और कई वर्षों के बाद पुनः एक-दूसरे से मिलते हैं। वे एक-दूसरे से पूछते हैं कि क्या कर रहे हो। उनमें एक सांख्यिकी में शोधकर्ता है और अपने मित्र को अभी-अभी छपा अपना शोध पत्र दिखाता है। उसका मित्र लेख में वर्णित नॉर्मल वितरण (normal distribution) के बारे में पूछता है, और पहला मित्र उसे किसी क्षेत्र में रहने वाले पुरुषों की लम्बाई के वितरण के उदाहरण से समझाता है। दूसरा मित्र तब पूछता है कि इस वितरण में प्रयुक्त संकेत चिन्ह π का क्या अर्थ है। जब उसे यह बताते हैं कि यह एक वृत्त की परिधि और उसके व्यास का अनुपात है, तो उसे विश्वास नहीं होता है। “तुम मुझसे मज़ाक कर रहे हो। वृत्त की परिधि का पुरुषों की लम्बाई से क्या सम्बन्ध?” विगनेर इस पर टिप्पणी करते हैं कि मित्र का ऐसा सोचना सहज बोध यानी कॉमनसेंस के अनुसार सही ही है। इस उदाहरण के द्वारा वे अपनी इस मुख्य थीसिस का प्रतिपादन करते हैं कि गणितीय निर्मितियाँ (mathematical construct) बहुत अनपेक्षित जगहों पर मिल जाती हैं, और वे भौतिक जगत का अत्यन्त परिशुद्ध वर्णन करने में मदद करती हैं।
विगनेर इसके बाद, ‘गणित’ और ‘विज्ञान’ शब्दों की व्याख्या करते हैं। इनका संक्षिप्त उल्लेख यहाँ भी करना आवश्यक है। वजह यह है कि इन शब्दों के क्या अर्थ हैं इसका कोई सर्वसम्मत उत्तर नहीं है। और यही नहीं, इनके मतलब समय के साथ बदलते रहे हैं।

उदाहरण के तौर पर, ओम के नियम के लिए ख्यातिप्राप्त वैज्ञानिक जॉर्ज ओम, ने बिजली के तारों में विद्युत प्रवाह विषय पर लिखी अपनी पुस्तक में कहा कि उनका विश्वास है कि उनकी शोध भौतिक विज्ञान के एक क्षेत्र को गणित का भाग बना देगी, जो अब तक गणित का भाग नहीं था।6 यह बात अब से लगभग दो सौ वर्ष पूर्व ही लिखी गई थी, पर यह बात आज के पाठक को काफी अटपटी लगती है। ओम का नियम तो भौतिक विज्ञान का नियम है। यह गणित का भाग कब से हो गया? स्पष्ट रूप से, ओम द्वारा प्रयुक्त गणित शब्द का अर्थ आज के प्रयोग से भिन्न है। हमें स्पष्ट करना पड़ेगा कि हम किस ‘गणित’ की बात कर रहे हैं।

मेरा अनुमान है कि ओम ने ‘गणित’ का उसी अर्थ में प्रयोग किया जिस अर्थ में आज के कुछ विद्यार्थी करते हैं जब वे कहते हैं कि समीकरण ‘s=(gt²)/2’ तो गणित है पर इसी का समानार्थी वाक्य ‘मुक्त रूप से गिरते हुए पिण्ड के लिए त्वरण अचर है’ गणित नहीं है। यहाँ पर ये विद्यार्थी भौतिक शास्त्र के नियमों के वर्णन में समीकरणों के उपयोग को गणित कहते हैं। पर यह सिर्फ गणित की भाषा का प्रयोग है; वर्णन का विषय गणित नहीं है। हम ‘गणित’ शब्द का प्रयोग इस अर्थ में नहीं करेंगे।
विगनेर द्वारा दी गई गणित की व्याख्या को समझना कुछ कठिन है: “गणित, कुछ विशेष परिभाषित नियम और उन पर कुशल संक्रियाओं का विज्ञान है।”* इन संरचनाओं और संक्रियाओं के उदाहरण के तौर पर विगनेर सम्मिश्र संख्याओं (complex numbers), बीजगणित, और रेखीय ऑपरेटर्स (linear operators) का उल्लेख करते हैं। वह यह भी ध्यान दिलाते हैं कि कौन-सी निर्मितियाँ उपयोगी सिद्ध होंगी, इसका पता गणित के स्वयंसिद्ध सत्य (एग्ज़ीयम्स) द्वारा नहीं किया जा सकता। गणित की विज्ञान में उपयोगिता के लिए इस चयन का सही होना आवश्यक है, और यह चयन गणित के ढाँचे से बाहर है। “गणितज्ञ, इस प्रकार की अतिरिक्त निर्मितियों के बिना केवल कुछ मुठ्ठी भर रुचिकर प्रमेयों की ही स्थापना कर पाएगा।” इन निर्मितियों की उपयोगिता का पूरा श्रेय सिर्फ गणित को देना ठीक नहीं लगता।

विज्ञान के सम्बन्ध में विगनेर नोट करते हैं कि, हमारे चारों तरफ फैला जगत ज़्यादातर समझ के परे है, पर इस सिरदर्द देने वाली जटिलता के बीच कुछ नियम देखे जा सकते हैं। यह ही प्रकृति के नियम हैं, जैसे ग्रहों की गति से सम्बन्धित केपलर के नियम। विगनेर के अनुसार, यह चमत्कार ही है, और पूरी तरह से अनपेक्षित है, कि ऐसे कुछ नियम हैं और वे सब जगह, सब समय लागू रहते हैं। इससे भी अधिक विस्मय की बात है कि मनुष्य इन नियमों को खोज पाता है। इन नियमों के अध्ययन को ही विगनेर विज्ञान कहते हैं।
इस लेख के प्रारम्भ में दिए गैलिलियो के कथन के विषय में विगनेर कहते हैं, “एक भौतिकशास्त्री प्रकृति के नियमों को प्रतिपादित करने में कुछ गणितीय निर्मितियों का प्रयोग करता है, और गणितज्ञों द्वारा अध्ययन की गई निर्मितियों का केवल एक छोटा-सा भाग ही भौतिक विज्ञान में प्रयोग किया गया है। भौतिक विज्ञान में वैज्ञानिक द्वारा प्रकृति के अनुमानित नियमों के गणित की भाषा में प्रतिपादन को कई बार आश्चर्यजनक सफलता मिली है।”
वह इस आश्चर्यजनक सफलता के उदाहरण के तौर पर क्वाण्टम मैकेनिक्स में हीलियम परमाणु की निम्नतम उर्जा और लैम्ब शिफ्ट के आकलन का ज़िक्र करते हैं और कहते हैं कि, “भौतिक विज्ञान के नियमों के प्रतिपादन में गणित की उपयोगिता हमारे लिए चमत्कार और दैवी भेंट है जिसे न तो हम ठीक से समझते हैं और न ही हम उसके योग्य हैं। हमें इसका आभारी होना चाहिए और आशा करनी चाहिए कि यह भविष्य में भी कारगर रहेगी।”

एबट का विपक्षी दृष्टिकोण
अब मैं संक्षेप में एबट की विचारधारा का ज़िक्र करता हूँ। एबट दो परस्पर विपरीत दार्शनिक विचारधाराओं की बात करते हैं जिनमें से एक को वे प्लेटोवादी और दूसरे को प्लेटोविरोधी नाम देते हैं।
ग्रीक दार्शनिक प्लेटो ने ज्ञानेन्द्रियों से प्राप्त हमारे संसार के बारे में हमारे बोध की अपूर्णता की बात की थी। उन्होंने हमारी तुलना एक काल्पनिक गुफा में रहने वालों से की जो अपनी गुफा के बाहर कभी गए ही नहीं हैं और गुफा के बाहर के संसार का ज्ञान, जैसे उड़ते हुए पक्षी, उनकी गुफा की दीवारों पर पड़ने वाली परछाइयों को देखकर ही कर पाते हैं। इस प्रकार, वे केवल गुफा की दीवार पर पड़ने वाली परछाइयों को देख सकते हैं और असली पक्षियों का सीधा अनुभव उनकी ज्ञानेन्द्रियों द्वारा असम्भव है। इस उदाहरण से प्लेटो ने निष्कर्ष निकाला कि हमारी ज्ञानेन्द्रियों के बोध से परे भी संसार है और वह ही वास्तविक संसार है तथा जिसका हमें अपनी ज्ञानेन्द्रियों द्वारा बोध होता है, वह वास्तविक संसार की छाया मात्र है।

इस विचार श्रखला के अनुसार, गणितीय आकार और संरचनाएँ, जैसे कि पूर्णांक इस वास्तविक बाह्य संसार का अंश हैं और उनका अस्तित्व है, चाहे कोई छाया को देखे या न देखे। इसी तरह, गणितीय अंकों, जैसे 7 और π का अस्तित्व तब भी था जब मानव जाति पृथ्वी पर अस्तित्व में भी नहीं थी। मैंने लेख की शुरुआत में एक लाख वर्ष का अन्तराल इसीलिए चुना था। यह अन्तराल बिग बैंग की आयु या पृथ्वी की आयु से बहुत कम है (पृथ्वी की आयु लगभग 400 करोड़ वर्ष है)। अब से एक लाख वर्ष पहले अधिकतर डायनासॉर मर चुके थे, पर मानव जाति और अन्य वानरों में ज़्यादा फर्क नहीं था।

इसके विपरीत दृष्टिकोण है कि हमारा सारा गणित मानव जाति के सांस्कृतिक विकास का ही फल है। गणित के सारे आकार और निर्मितियाँ भौतिक जगत के वर्णन के लिए मनुष्य द्वारा ही बनाई गई हैं। किसी प्लेटोविरोधी के मतानुसार, इस अखिल ब्रम्हाण्ड में कोई भी त्रुटिहीन वृत्त नहीं है, और अंक πसिर्फ एक उपयोगी मानसिक निर्मिति है।

एबट के अनुसार, उनके अनुमान में गणितज्ञों में लगभग 80 प्रतिशत लोग प्लेटोवादी होते हैं, पर इंजीनियरिंग या तकनीकी क्षेत्रों में काम करने वाले अक्सर प्लेटोविरोधी होते हैं। वह कहते हैं कि भौतिकी के वैज्ञानिक अक्सर ‘छुपे हुए प्लेटोविरोधी’ होते हैं: ऊपरी दिखावे में औरों के सामने वे अपने को प्लेटोवादी कहते हैं, पर अपने दिल में उनका विश्वास इस बात पर पक्का नहीं है।
गणित की अनपेक्षित उपयोगिता के विषय में एबट का मत है कि हमारे संसार की अधिकांश समस्याओं को समझने या उनके हल की खोज में गणित बहुत अधिक सफल नहीं है। यह सफलता प्रभावशाली तभी दिखती है जब हम केवल उन उदाहरणों पर ध्यान केन्द्रित करें जहाँ पर वह सफल रही है। जीव विज्ञान के वर्णन में गणित की उपयोगिता बहुत ज़्यादा नहीं है; मनोविज्ञान और समाजशास्त्र में तो और भी कम। हमने बहुत-से निराशाजनक उदाहरणों को छोड़, सारा ध्यान उन बहुत कम संख्या के उदाहरणों पर सीमित कर लिया है जहाँ गणित उपयोगी रहा है।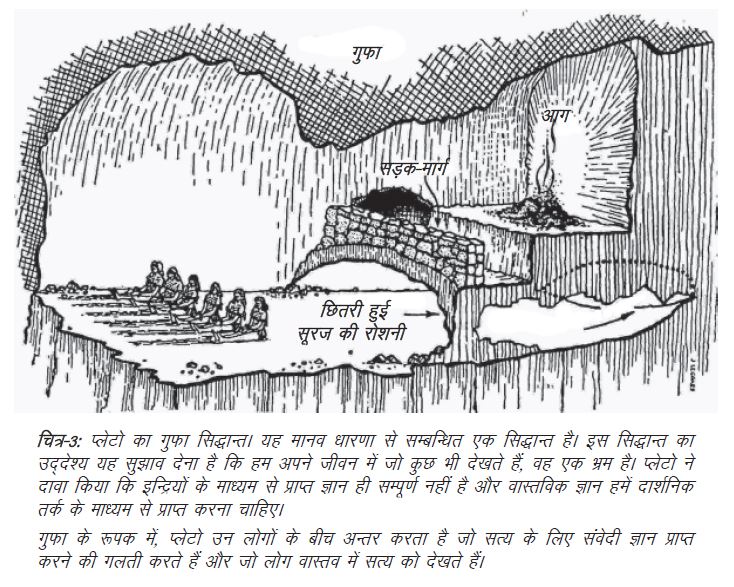

विगनेर द्वारा वर्णित केपलर की समस्या पर एबट का मत है कि यह एक खास तौर पर चुना गया उदाहरण है और हमारे पूर्ण वर्ग संख्याओं से लगाव पर आधारित है। असल में, ग्रहों की कक्षा कुछ हद तक ही दीर्घवृत्त के आकार की होती है। वैसे भी, न्यूटन का गुरुत्वाकर्षण सिद्धान्त, आइंस्टाइन के गुरुत्वाकर्षण सिद्धान्त का एक सन्निकटन (approximation) मात्र है। हम मानते हैं कि यह काफी अच्छा सन्निकटन है पर स्पष्ट रूप से यह इस बात का कोई सबूत नहीं है कि गणित का प्रयोग प्रकृति के नियमों के सत्य तक पहुँचने का एक जादुई नुस्खा है।
प्लेटोविरोधी मत के अनुसार, गणित मानव जाति की कल्पना का फल है। हमारे समस्त भौतिक विज्ञान द्वारा प्रतिपादित ‘प्रकृति के नियम’ एक सरलीकरण/ आदर्शीकरण/ सन्निकटन (simplification/ idealization/ approximation) की प्रक्रिया पर आधारित हैं और इस प्रकार वे कभी अपने आप में पूर्णतया त्रुटिरहित या अपरिवर्तनीय होने का दावा नहीं करते। प्रकृति की नियमितताओं (regularities) का वर्णन करने के लिए गणित को मनुष्य द्वारा ईजाद किया गया है और वह ब्रह्माण्ड की नियमितताओं के वर्णन की एक उपयोगी युक्ति मात्र है।

मेरा दृष्टिकोण
यदि गणित मनुष्य के अस्तित्व पर निर्भर नहीं है, तो हम यह देखने की कोशिश कर सकते हैं  कि अन्य जन्तुओं जैसे कीड़े-मकोड़े, मेंढक, चिड़ियों या कुत्ते-बिल्लियों के जीवन में गणित का क्या रोल है या क्या रोल था। यही कारण है कि मैंने इस लेख की शुरुआत में ही एक लाख वर्ष पहले का समय चुना।
यदि कीड़ों और बैक्टीरिया की बात करें, यह कह पाना कठिन है कि गणित का उनके जीवन में कुछ रोल है। अगर पक्षियों की बात करें, तो उनके दिमाग का आकार कुछ बड़ा होता है और नर-मादा साथ-साथ रहकर बच्चों की देखभाल करते हैं। पक्षियों की कुछ प्रजातियों के बारे में देखा गया है कि यदि उनके घोंसले से एक अण्डा हटा दें, तो वे उत्तेजित हो गए दिखते हैं। इस बात से हम कह सकते हैं कि ये पक्षी दो अण्डों या तीन अण्डों में फर्क पहचान सकते हैं और इस आधार पर यह भी कह सकते हैं के वे तीन या चार की गिनती करना भी जानते हैं। चिड़ियों के मानसिक या भौतिक जीवन में गणित का इससे अधिक क्या रोल हो सकता है, इसकी कल्पना भी कठिन ही है।

अन्य जन्तुओं के जीवन में गणित के सम्भव रोल की चर्चा करने के पहले, यह उपयोगी होगा कि हम गणित के विभिन्न स्तरों के मध्य फर्क कर लें।
गणित के प्रयोग का सबसे पहला स्तर है, जिसे मैं गणित-पूर्व स्तर कहूँगा, अंकों और आकारों को पहचानने की जन्मजात क्षमता और गति के अनुमान की क्षमता। यह क्षमता मनुष्यों में ही नहीं, अन्य पशुओं में भी मिलती है। यह जैव-विकास का परिणाम है। यह जन्तुओं को अपने परिवेश में चलने-फिरने में, शिकार पकड़ने में, और शिकार बनने से बचने में काम आती है। इन सब कामों में यह स्पष्ट रूप से बहुत उपयोगी है। शायद जन्तुओं द्वारा प्रयुक्त गणित इस स्तर से बहुत आगे नहीं जाता है। इन जन्तुओं में मैं स्तनधारी जन्तु जैसे कुत्ते, घोड़े और यहाँ तक कि, वानरों को भी शामिल कर रहा हूँ।
गणित का दूसरा स्तर प्राथमिक कक्षाओं में बच्चों को पढ़ाया जाने वाला गणित है। इसमें पूर्णांक या भिन्नों को जोड़ने, गुणा करने इत्यादि जैसी कुछ सामान्य संक्रियाएँ शामिल हैं और इसके अतिरिक्त कुछ भी नहीं।

तीसरे स्तर के गणित में बीजगणित में संकेत चिन्हों का प्रयोग, प्रमेय (theorem) और उपपत्ति (proof) के अर्थ, और √2 जैसे अपरिमेय (irrational) अंकों का ज्ञान शामिल है। इसे मैं हाईस्कूल स्तर का गणित कहूँगा। यह वह गणित है जो अब हम हाईस्कूल के छात्र-छात्राओं को पढ़ाते हैं और अब से कुछ हज़ार वर्ष पूर्व तक मानव जाति भी सिर्फ इतना ही गणित जानती थी। यह वाणिज्य और अभियांत्रिकी के लिए उपयोगी गणित है। चीज़ें खरीदने और बेचने के लिए हमारे लिए अंकों को जोड़ने और गुणा करने आदि की जानकारी ही पर्याप्त है। ऐसे घर या महल बनाने के लिए जो गिर न जाएँ, हमें ज्यामिति की कुछ अवधारणाओं के प्रयोग की ज़रूरत पड़ सकती है। कोई खम्भा या छत कितना भार सँभाल सकेगी, यह उसकी मोटाई या लम्बाई की कुछ घातों पर निर्भर करता है और इसमें हम तृतीय स्तर के गणित का उपयोग करते हैं। इस उपयोग में गणित बहुत कारगर है, पर शायद यह कारगर होना अनपेक्षित नहीं है।

इसके ऊपर के स्तर को मैं उच्चतर गणित कहूँगा। इसमें वह सब विषयवस्तु शामिल है, जिन्हें निचले स्तरों में नहीं लिया गया। स्पष्टतः, विभिन्न स्तरों की सीमाएँ निश्चित करने में हमें कुछ हद तक चयन की स्वतंत्रता है। उदाहरण के तौर पर, मैंने अवकलन या समाकलन (differentiation or integration) को तृतीय स्तर में शामिल नहीं किया पर मैं कर सकता था ।
जैव विज्ञानी जानते हैं कि मनुष्य के अलावा अन्य जन्तुओं में द्वितीय स्तर के गणित के प्रयोग का कोई विश्वसनीय प्रमाण अब तक नहीं मिला है। इस स्थिति में, यह कहना मुश्किल है कि मानव-हीन जगत में हम किस गणित की बात कर सकते हैं! (किसी और ग्रह में रहने वाले अतिविकसित क्लिंगॉन जाति के लोग कैसा गणित प्रयोग करते होंगे, इस विषय की चर्चा हम विज्ञान-गल्प के पाठकों के लिए छोड़ देते हैं।)

यदि यह कथन आपको बहुत अधिक मानवकेन्द्रित (एंथ्रोपोसेंट्रिक) लगे, तो मैं यह भी कहना चाहूँगा कि सवाल मानव या गैर-मानव का नहीं है। गणितीय क्षमता तो सब मनुष्यों में भी बराबर नहीं होती। विश्व के सभी देशों में हाईस्कूल के लगभग आधे विद्यार्थी तृतीय स्तर की गणित को समझने में कठिनाई महसूस करते हैं। यहाँ यह कहना भी ज़रूरी है कि गणित में पटुता के बिना भी उनके समाज में योगदान देने की या जीवन का आनन्द लेने की क्षमता में कोई कमी नहीं आती है।
किसी चीज़ को देखने पर पहचानने, और देखी हुई वस्तु में कुछ फर्क को नज़रअन्दाज़ करने (noise filtering), या उसके एक आदर्श प्रतिरूप की कल्पना कर लेने (idealization) की सामर्थ्य मानव जाति ने जैव-विकास से पाई है। यह सामर्थ्य अत्यन्त जन्मजात है और इसका एक जाना-पहचाना उदाहरण है कनिषा त्रिभुज के नाम से विख्यात दृष्टिभ्रम (चित्र-5)। दोषयुक्त आँकड़ों (data) से एक उपयोगी जानकारी छानकर निकाल लेने की क्षमता निश्चय ही लाभदायक है, और अन्य जानवरों में भी पाई जाती है। अगर कोई हिरण आंशिक रूप से घास में छुपे शेर को पहचान लेता है तो यह उसे जीवित रहने में लाभकर है।

ग्रहों की कक्षाओं में दीर्घवृत्त को देखना, इसकी सन्निकटता और आदर्श प्रतिरूप ढूँढ़ना (approximation and idealization) भी इसी प्रवृत्ति का उदाहरण है। फिर भी, शायद हिरण में इस सामर्थ्य को गणित कहना ठीक नहीं होगा। मुझे लगता है कि विगनेर जिस ‘गणित की अनपेक्षित उपयोगिता’ की बात कर रहे थे, वह उच्चतर गणित था। जीव विज्ञान, मनोविज्ञान और भूगर्भ विज्ञान जैसे क्षेत्रों में गणित बहुत ज़्यादा उपयोगी नहीं है। अतः, मैं मान लेता हूँ कि यद्यपि विगनेर ‘विज्ञान’ की बात कर रहे थे, वे मुख्यतः भौतिक विज्ञान के बारे में ही सोच रहे थे। भौतिक विज्ञान में भी, कई क्षेत्रों में हम गणित के उपयोगी होने की आशा कर सकते हैं, जैसे क्रिकेट के खेल में आने वाली बॉल की गति के अनुमान के लिए। पर यह जानने के लिए कि क्रिकेट के खेल में गणित बहुत उपयोगी नहीं है, आपके लिए तेंदुलकर या कोहली होना ज़रूरी नहीं है। मैं एबट से पूरी तरह से सहमत हूँ कि गणित की अनपेक्षित उपयोगिता, अपने विचारक्षेत्र को बहुत सीमित करने का ही परिणाम है। यदि हम केवल उन विषयों की बात करें, जहाँ गणित बहुत उपयोगी है, तो यह उपयोगिता तो अपेक्षित ही है, अनपेक्षित नहीं।

इससे पहले हमने समीकरण s=(gt²)/2 की बात की थी। इस समीकरण में अन्तर्निहित एक महत्वपूर्ण पूर्वधारणा (assumption) है कि चली गई दूरी को एक वास्तविक संख्या (real number) द्वारा अभिव्यक्त किया जा सकता है। सवाल उठता है कि हवा में उड़ती हुई एक बॉल द्वारा चली गई दूरी के बारे में क्या यह सच है? यदि दूरी को सेंटीमीटर में लिखें, तो क्या इसे दशमलव के 15वें स्थान तक निर्धारित करना सम्भव है? यहाँ हम प्लांक लेन्थ स्केल (10-35 मीटर) की बात नहीं कर रहे हैं जब गुरुत्वाकर्षण के क्वाण्टम सिद्धान्त के अनुसार अन्तरिक्ष की संरचना में बहुत फर्क आ जाता है। फिर भी, यह एक परमाणु के आकार का भी 105वाँ अंश है। थोड़ा-सा सोचने पर हम यह समझ पाएँगे कि इस परिशुद्धता तक बॉल के द्रव्यमान केन्द्र की परिभाषा भी कठिन है। उसको उपकरणों द्वारा नापने की तो बात ही छोड़ दें। बॉल परमाणु उष्मीय गति के कारण इधर-उधर हिलते-डुलते रहते हैं और इस गति का आयाम 10-11 मीटर है। जब बॉल हवा में चलती है, तो हवा के साथ घिसने के कारण कुछ परमाणु बॉल से अलग होकर हवा के साथ बह जाते हैं, और यह कहना मुश्किल है कि द्रव्यमान केन्द्र के आकलन में इनका भी योगदान होना चाहिए या नहीं। हम यहाँ इसी बात के महत्व को दिखा रहे हैं कि हम भौतिक जगत की समस्या का सरलीकरण करते हैं और उसका एक आदर्श प्रतिरूप (idealized model) बनाते हैं जिसमें चली गई दूरी को एक वास्तविक संख्या द्वारा निरूपित करते हैं। इसके बाद ही कुछ गणित की युक्तियों द्वारा इस सरलीकृत प्रश्न का हल निकाला जा सकता है।

विगनेर इस बात की गम्भीरता से वाकिफ थे कि जिन प्रश्नों का हल गणित की मदद से मिल सकता है, वे सब सम्भव प्रश्नों का एक छोटा-सा अंश हैं। उसी लेख में विगनेर ने लिखा, “प्रकृति के समस्त नियम कुछ कथन हैं जो वर्तमान की स्थिति की कुछ जानकारी के आधार पर आगे भविष्य में क्या होगा, इस की जानकारी देते हैं। लेकिन वर्तमान स्थिति ऐसी क्यों है? संसार की वर्तमान स्थिति, जैसे कि पृथ्वी ग्रह का वेग कितना है, और सूरज क्यों है और हमारे चारों ओर का जगत ऐसा क्यों है, इस विषय में प्रकृति के नियम कुछ नहीं कहते।”
अब मैं प्लेटोवादी विश्व में अस्तित्व के अर्थ की बात करूँगा। हमारा विश्वास कि सामने रखी मेज़ का अस्तित्व है, उसको देखने और छूने के हमारी ज्ञानेन्द्रियों के अनुभव पर आधारित है। यह प्रत्यक्ष इन्द्रियजनित अनुभव नए अधिक संवेदनशील उपकरणों जैसे सूक्ष्मदर्शी, एक्स-रे कैमरा, रासायनिक सेंसरों और पार्टिकिल कोलाइडर आदि से आवश्यकतानुसार और बढ़ाया जा सकता है। विज्ञान इस भौतिक जगत की वस्तुओं जैसे मेज़ या बृहस्पति ग्रह या हिग्स बोसॉन के बारे में बात करता है। प्लेटो ने एक बहुत ही भ्रामक उपमा का प्रयोग किया था, और गुफावासियों के छाया सम्बन्धी अनुमान को छायाओं से ऊँचा दर्ज़ा दिया। हम चाहें तो मेज़ के विचार को मेज़ से ज़्यादा ऊँचा दर्ज़ा दे सकते हैं। पर क्या इससे मेज़ के विचार का अस्तित्व मेज़ से अधिक वास्तविक हो जाएगा?

समापन
गणित और भौतिक विज्ञान के बीच सम्बन्धों की बात गणितशास्त्रीयों और वैज्ञानिकों के बीच के संवाद की बात किए बिना अधूरी रह जाएगी। यहाँ मैं चेन निंग यांग द्वारा वर्णित कहानी को पुनः दोहराना चाहूँगा। यह एक भौतिक विज्ञानी के बारे में है जो वैज्ञानिक सम्मेलनों में भाग लेने, और अलग-अलग जगहों पर भाषण देने के लिए पूरे अमेरिका में घूम रहा है। वह एक विश्वविद्यालय से जुड़े छोटे शहर में आता है, एक होटल में ठहरता है और अपने गन्दे कपड़ों को धोने के लिए उन्हें एक झोले में लेकर उपयुक्त लॉण्ड्री की तलाश में अपरिचित सड़कों और गलियों में भटक रहा है। काफी दूर इधर-उधर पैदल भटकने के बाद अन्ततः उसे एक दुकान दिखाई पड़ती है जिस पर साइनबोर्ड लटका है, ‘यहाँ कपड़े धोए जाते हैं’। कुछ राहत महसूस करता वह दुकान के अन्दर घुसता है और अपने गन्दे कपड़ों से भरे झोले को दुकाने के काउण्टर पर रख देता है। काउण्टर के दूसरी तरफ कुछ चीनी जैसी शकल-सूरत का आदमी बैठा होता है। वह कुछ रूखेपन से पूछता है, “तुम्हें क्या चाहिए?” वैज्ञानिक कहता है, “मुझे अपने ये कपड़े धुलवाने हैं।” दुकान के काउण्टर पर बैठा चीनी आदमी कहता है, “हम यहाँ कोई कपड़े नहीं धोते हैं।” वैज्ञानिक को बहुत गुस्सा आता है और वह दुकान पर लटके साइनबोर्ड की तरफ इशारा करके कहता है, “लेकिन यहाँ तो साफ-साफ लिखा है कि यहाँ कपड़े धोए जाते हैं।” काउण्टर के पीछे बैठा चीनी व्यक्ति मुस्कुराता है, “अरे! वह…। यहाँ पर हम सिर्फ साइनबोर्ड बनाते हैं।”

मुझे यह कहानी पसन्द है क्योंकि यह भौतिकी के वैज्ञानिकों की गणितज्ञों से अपेक्षित मदद न मिलने पर उनके मन में पैदा हुई कुण्ठा को दिखाती है। अक्सर किसी भी प्रश्न पर गणितज्ञों और भौतिक वैज्ञानिकों के सोचने का ढंग अलग होता है।
अब इस लेख के शुरू में π के अस्तित्व के बारे में उठाए प्रश्न पर लौटते हैं। मैंने आपको समझाने का प्रयास किया है कि इस प्रश्न का उत्तर ‘नहीं’ ही होना चाहिए। एक मानसिक अवधारणा का अस्तित्व तब ही कहा जा सकता है जब इसे किसी ने पहली बार सोचा हो। इससे भी पहले इसके अस्तित्व का कोई अर्थ नहीं है। जो बात यहाँ  के लिए कही गई, वही गणित की अन्य जटिलतर निर्मितियों और संरचनाओं के लिए भी सच है। इस वृहत्तर थीसिस पर विभिन्न पहलुओं और दृष्टिकोणों से चर्चा के लिए पुस्तक7 में उपलब्ध निबन्धों के संग्रह को देखें। यह इंटरनेट पर निःशुल्क उपलब्ध है। शायद आपने महान गणितज्ञ क्रोनेकर का यह कथन पढ़ा होगा, “ईश्वर ने सिर्फ पूर्णांक बनाए। बाकी सब गणित मनुष्य का बनाया हुआ है।” लेकिन मुझे लगता है कि ईश्वर भी मनुष्य की बनाई हुई निर्मिति है। मैं इसी निबन्ध संग्रह में छपे एस. वेनमैकर्स8 द्वारा लिखे एक निबन्ध की दो पंक्तियों के साथ इस लेख का अन्त करता हूँ:
“भौतिक विज्ञान के नियम गणित की मदद से अभिव्यक्त किए जा सकते हैं; यह इसी बात का द्योतक है कि नियमितताओं का (यह) विवरण हमारा ही बनाया हुआ है। जब हम प्रकृति की किताब को, जिसकी बात गैलिलियो ने की थी, खोलते हैं, तो उसे अपनी ही हस्तलिपि से भरा पाते हैं।”

दीपक धर: इलाहाबाद विश्वविद्यालय से स्नातक और भारतीय तकनीकी संस्थान (आई.आई.टी.), कानपुर से स्नातकोत्तर। कैलिफोर्निया इंस्टीट्यूट ऑफ टेक्नोलॉजी से पीएच.डी. करने के बाद 1978 से 2016 तक टाटा मूलभूत अनुसन्धान संस्थान (TIFR), मुम्बई में कार्यरत रहे। वर्तमान में भारतीय विज्ञान शिक्षा एवं अनुसन्धान संस्थान, पुणे (IISER, Pune) के भौतिकी विभाग में आचार्य हैं।
अँग्रेज़ी से अनुवाद: इष्ट विभु: लखनऊ विश्वविद्यालय, लखनऊ से भौतिक विज्ञान में पीएच. डी.। वर्तमान में युवराज दत्त महाविद्यालय, लखीमपुर खीरी में भौतिक विज्ञान के एसोसिएट प्रोफेसर के पद पर कार्यरत हैं।

अन्त टिप्पणियाँ:
1) W. Dubislav, Die Philosophie der Mathematik in der Gegenwart (Berlin: Junker and Dunnhaupt Verlag, 1932), p.1, सन्दर्भ (3) से|
2) Philosophy is the misuse of a terminology which was invented just for this purpose.
3) कॉर्ल एफ़. गाउस, वोल्फ़गांग सारटोरियस फॉन वाल्टर्सहाउज़ेन द्वारा लिखित “Gauss zum Gedächtniss (1856)” से; “Mathematics is the queen of sciences and number theory is the queen of mathematics” विकीपीडिया से।
4) यूजीन िवगनेर, Unreasonable Effectiveness, https://plus.maths.org/content/unreasonable-effectiveness
5) डैरेक एबट; Reasonable  Ineffectiveness, https://pdfs.semanticscholar.org/462d/7b6b1ee8243b6aa8897be3cf306239fb43c6.pdf
6) जॉर्ज ओम, “The Galvanic Circuit, Investigated Mathematically, Ed. Richard Taylor (New York, Johnson Reprint of the 1841 edition, 1966)” मूल जर्मन में 1826 में प्रकाशित पुस्तक का अनुवाद|
7) Trick or Truth: The Mysterious Connection Between Physics and Mathematics, Eds. Anthony Aguirre, Brendan Foster and Zeeya Merali, Springer, 2016. https://www.nwcbooks.com/download/trick-or-truth/
8) एस. वेनमैकर्स, Children of the Cosmos, सन्दर्भ (7) से|