--अंजु दास मानिकपुरी भाग - 2
इस लेख की पहली किश्त में हमने देखा कि 17वीं सदी में प्रकाश की ‘अनन्त गति’ को नापने के कुछ प्रयास किए गए, जिनमें गैलीलियो एवं रोमर के नाम प्रमुख हैं। गैलीलियो ने प्रकाश की गति को नापने की कोशिश धरती पर ही की थी। लेकिन रोमर ने बृहस्पति के उपग्रह ईवो को लगने वाले ग्रहण के समय को आधार बनाकर प्रकाश की गति के लिए एक ठोस आँकड़ा निकालने का प्रयास किया। इसके बाद काफी साल प्रकाश की गति को लेकर कोई उल्लेखनीय पहल नहीं हुई। शायद लोग रोमर के प्रयास को भूलने भी लगे थे, लेकिन 18वीं सदी में समय ने एक बार फिर करवट बदली। इस बार एक नई समस्या पर काम चल रहा था। तारे पृथ्वी से काफी दूरी पर हैं, यह तो सभी जानते थे लेकिन यह दूरी वास्तव में कितनी है, इसे कैसे पता किया जाए?
पृथ्वी साल भर में सूरज की एक परिक्रमा पूरी करती है। इस एक परिक्रमा के दौरान विविध तारों का अवलोकन करने से समझ आया कि (अन्य तारों की स्थिति की तुलना में) कुछ तारों की आकाशीय स्थिति में काफी बदलाव होता है व कुछ तारों में नाममात्र का बदलाव भी नहीं होता। इसे लेकर एक विचार यह भी था कि पास के तारों की स्थिति में बदलाव ज़्यादा होगा और दूरस्थ तारों में बदलाव नाममात्र। कुछ खगोलविद इसी सन्दर्भ में पैरेलेक्स विधि पर काम कर रहे थे, जिसके तहत किसी अवलोकनकर्ता द्वारा (किसी बहुत दूर स्थित तारे की स्थिति की तुलना में) किसी तारे की आज की आकाशीय स्थिति और छह महीने बाद की आकाशीय स्थिति की तुलना कर कुछ गणनाएँ करके तारे की दूरी मालूम करने की कोशिश की जा सकती थी। तारों की दूरी और निकटता को लेकर कुछ कयास थे, लेकिन पास मतलब कितना पास और दूर मतलब कितना दूर, यह नहीं मालूम था। और इसी दौरान और इस सबकी वजह से प्रकाश की गति को लेकर भी कुछ विचार उभरने लगे। 
सन् 1728 में इंग्लैंड के खगोलशास्त्री जेम्स ब्रेडली तारों के पैरेलेक्स का अध्ययन कर रहे थे। इस अध्ययन के दौरान उन्हें समझ आया कि कुछ तारों की आकाशीय स्थिति में बदलाव 20 सेकण्ड (सेकण्ड - कोण नापने की एक इकाई) तक मिल रहा था। उदाहरण के लिए, उन्होंने पाया कि ड्रेको नक्षत्र (तारा समूह) में एक तारे की स्थिति साल भर बदलती रहती है। हैरान करने वाली बात यह थी कि तारे में विचलन की दिशा पृथ्वी की गति की दिशा के विपरीत होनी चाहिए थी, परन्तु जब उन्होंने टेलिस्कोप से तारे के कई अवलोकन किए तो पाया कि तारे के विस्थापन की दिशा और पृथ्वी के घूमने की दिशा एक ही है। ब्रेडली समझ गए कि यह पैरेलेक्स की वजह से सम्भव नहीं है। इस विचलन को aberration of starlight कहा गया। ब्रेडली इस सवाल से लम्बे समय तक जूझते रहे लेकिन जल्द ही उन्हें इस बात का भान हो गया कि तारे के इस विस्थापन (aberration) का सम्बन्ध पृथ्वी की परिभ्रमण गति से अवश्य है।
अन्ततः इसे समझने के लिए ब्रेडली ने बारिश से बचने के लिए खुले हुए छाते का उदाहरण देते हुए एक परिकल्पना प्रस्तुत की। मान लीजिए कि आप बारिश में खड़े हैं और बारिश की बूँदे सीधी नीचे की ओर गिर रही हैं। ऐसी स्थिति में आप छाते को अपने सिर के ठीक ऊपर सीधा रखेंगे – ऐसा करने से आप बारिश से बचे रहेंगे। अब अगर आप इस बारिश में चलने लगें तो आपके छाते के आगे गिरने वाली बूँद आप से टकराएगी क्योंकि जब तक वह बूँद नीचे को आएगी, आप आगे को कदम बढ़ाकर उसके रास्ते में आ जाएँगे। इसलिए अगर आप बारिश में चलते हैं तो अपने आप को बारिश से बचाने के लिए छाते को थोड़ा-सा आगे को झुकाना पड़ेगा ताकि आगे गिरने वाली बूँदें आपके चलने के बावजूद आपको भिगोएँ नहीं। सही ही है, क्योंकि आप आगे गिरने वाली बूँदों की तरफ जा रहे हैं, और आपके पीछे गिरने वाली बूँदों से दूर।
अब आप सोचकर देखिए, अगर आप तेज़ी-से चल रहे हैं तो आपको छाता ज़्यादा आगे को झुकाना पड़ेगा। अगर बूँदें धीमी गिर रही हैं तो भी आपको छाता आगे को ज़्यादा झुकाना पड़ेगा। यानी कि अगर आप अपनी गति जानते हैं, और बारिश की बूँदों के गिरने की गति जानते हैं तो आप पता कर सकते हैं कि आपको छाता कितने कोण पर तिरछा रखना होगा। और इसी तर्क से, अगर आप अपनी चाल जानते हैं और आपको यह पता है कि कितने कोण पर छाता तिरछा रखकर आप बारिश से बच पा रहे हैं, तो इन दोनों का इस्तेमाल करते हुए आप बारिश की बूँदों के गिरने की गति पता कर सकते हैं।
ब्रेडली ने इसी तर्क को आगे बढ़ाते हुए माना कि तारों से आने वाला प्रकाश भी बारिश की बूँदों की तरह पृथ्वी पर गिरता होगा। जिस तरह हम बारिश की बूँदों से बचने (यानी वे छाते पर गिरें, यह सुनिश्चित करने) के लिए छाते को एक खास कोण पर रखते हैं, उसी तरह से घूमती धरती पर किसी तारे के प्रकाश को पकड़ने के लिए टेलिस्कोप को खास कोण पर रखना पड़ता है। इसी वजह से उन्हें तारों की स्थिति में अन-अपेक्षित विचलन मिल रहा था। उन्हें वह विचलन कोण तो मालूम था ही, साथ ही यह जानकारी भी थी कि पृथ्वी सूर्य के इर्द-गिर्द किस गति से घूमती है – तो इन दोनों आँकड़ों का इस्तेमाल करते हुए, ब्रेडली गणना कर पाए कि तारे से धरती पर प्रकाश किस गति से गिरता है। ब्रेडली ने प्रकाश की गति लगभग 1,76,000 मील या 2,84,000 कि.मी. प्रति सेकण्ड बताई, जो प्रकाश के वर्तमान परिशुद्ध मान से कुछ हज़ार कि.मी. कम है, परन्तु रोमर के आँकड़ों पर आधारित गणनाओं से कहीं बेहतर।
धरती पर गति नापने की कोशिश
रोमर और ब्रेडली, दोनों ने ही खगोलीय घटनाओं को आधार बनाकर प्रकाश की गति को नापा, जिसमें मापन की शुद्धता एवं सूक्ष्मता के कई कारक हमारे बस में नहीं होते। इसलिए कई वैज्ञानिक इस बारे में सोचने लगे थे कि क्या प्रकाश की गति को धरती पर नापा जा सकता है, क्या धरती पर मिली माप और खगोलीय विधियों से मिली माप लगभग एक जैसी होंगी या उनमें काफी अन्तर होगा। 
19वीं सदी के पूर्वार्द्ध में प्रकाश के कई गुणधर्मों को समझा जा रहा था, कई प्रकाशीय उपकरण जैसे कैमरा, स्पेक्ट्रोस्कोप आदि का उपयोग शुरू हो चुका था। लगभग इसी दौर में फ्रांस के अर्मांड हिप्पोलिट फीज़ो (Armand Hippolyte Fizeau 1819-96), कैमरा व फोटोग्राफी के अध्ययन में व्यस्त थे। असल में, फीज़ो प्रोफेसर लुईस डेगुरर की एक डेमो क्लास में उपस्थित थे, जहाँ उन्होंने देखा कि प्रोफेसर डेगुरर आयोडीन-युक्त कुछ रसायन की मदद से 30 मिनट में फोटो निकालकर लोगों को दिखाते थे। इस डेमो क्लास के बाद से ही फीज़ो सोचने लगे कि फोटोग्राफी की इस प्रक्रिया को सरल कैसे बनाया जाए, जिससे कम-से-कम समय में ज़्यादा फोटो निकाली जा सकें। उन दिनों फोटो खिंचवाने के लिए लोगों को एक ही पोज़िशन में काफी देर मूर्ति जैसे स्थिर बने रहना होता था। फीज़ो अपनी इस कोशिश में सफल भी हुए और ब्रोमीनयुक्त एक रसायन का इस्तेमाल करके 20 सेकण्ड में फोटो निकालकर दिखाई जो प्रोफेसर डेगुरर द्वारा लगाए गए समय के मुकाबले काफी कम था।
इस कोशिश और रुचि को आगे बढ़ाते हुए फीज़ो अपने दोस्त फूको के साथ खगोलीय पिण्डों की भी फोटो खींचना चाहते थे। इसी सन्दर्भ में वे एक अन्य खगोलशास्त्री एरगो (Francois Jean Arago) के सान्निध्य में आए और उनकी देखरेख में टेलिस्कोप में दिख रहे सूरज की फोटो खींची। यह फोटो उस समय की पहली खगोलीय या आकाशीय फोटोग्राफी थी। कैमरे का इस्तेमाल करते समय फ्लैश लाइट की चमक को देखकर फीज़ो के मन में सवाल कौंधा कि पृथ्वी पर प्रकाश की गति कितनी होगी।
एरगो के सान्निध्य में रहते हुए फीज़ो ने प्रकाश की प्रकृति को लेकर कण सिद्धान्त और तरंग सिद्धान्त की जद्दोजहद में लगे एरगो की कई रिपोर्ट्स को काफी बारीकी-से पढ़ा। उस समय प्रकाश की प्रकृति को लेकर अलग-अलग तर्क दिए जाते थे। कुछ तर्क इस तरह थे, जैसे यदि प्रकाश का कण सिद्धान्त सही है तो प्रकाश की गति सघन माध्यम में कुछ ज़्यादा होनी चाहिए, जैसे पानी में। इसी तरह प्रकाश यदि तरंग प्रकृति का है तो इससे उल्टा होना चाहिए अर्थात् सघन माध्यम में प्रकाश की चाल कम होनी चाहिए। उन्होंने अपने अवलोकन के आधार पर लिखा कि प्रकाश विरल माध्यम के बनिस्बत सघन माध्यम में तुलनात्मक रूप से धीमा हो जाता है।
सन् 1842 में क्रिश्चियन डॉप्लर ने नया विचार सामने रखा। जिसे बाद में डॉप्लर प्रभाव कहा गया। फीज़ो का मानना था कि डॉप्लर प्रभाव को प्रकाश पर भी लागू करना चाहिए क्योंकि वह भी एक तरंग की भाँति व्यवहार करता है। पर इसके लिए यह जानना ज़रूरी था कि प्रकाश की गति क्या है। यानी कि प्रकाश के कई गुणों का अध्ययन इसलिए नहीं हो पा रहा था क्योंकि प्रकाश की वास्तविक गति पता नहीं थी। बस, इन्हीं सब विचारों ने फीज़ो का ध्यान प्रकाश की गति की ओर खींचा। आइए, फीज़ो के इस प्रयोग को विस्तार से समझते हैं।
फीज़ो का तरीका
फीज़ो ने भी अपने प्रयोग के लिए गैलीलियो की तरह 1849 में पाँच मील की दूरी पर स्थित दो पहाड़ियों को चुना। गैलीलियो के प्रयोग में समस्या-मूलक प्रतिक्रिया समय को दूर करने के लिए फीज़ो ने दूसरी पहाड़ी पर एक दर्पण रख दिया जिससे टकराकर प्रकाश किरण तुरन्त परावर्तित हो जाती थी। यानी एक पहाड़ी से चमकाए गए प्रकाश की किरण को दूसरी पहाड़ी पर रखे दर्पण से टकराकर लौटने में लगा समय पता चल जाए, तो पहाड़ियों के बीच की दूरी को जानते हुए, प्रकाश की गति की गणना आसानी-से की जा सकती है।
चूँकि फीज़ो के समय प्रकाश की गति का कुछ अन्दाज़ा मिल गया था इसलिए यह स्पष्ट था कि इस प्रयोग में प्रकाश को लगने वाले समय (जो एक सेकण्ड के हज़ारवें हिस्से से भी कम होने वाला था) को उस समय मौजूद सबसे बेहतरीन घड़ी का इस्तेमाल करते हुए भी मापना सम्भव नहीं था। इस काम के लिए फीज़ो ने बहुत ही नायाब युक्ति लगाई। इस काम के लिए फीज़ो ने एक दाँतेदार पहिए का इस्तेमाल किया, जिसे इस तरह रखा गया कि दाँतेदार पहिए की किनार प्रकाश किरण के रास्ते में आए। यानी कि प्रकाश की किरण उस पहिए से आगे जाएगी कि नहीं, यह इस बात पर निर्भर करता कि उसके रास्ते में दाँता है, या दो दाँतों के बीच की खाली जगह यानी खाँचा है।
घूमता हुआ दाँतेदार पहिया इस पूरे उपकरण का महत्वपूर्ण भाग था। जब फीज़ो ने इस पहिए को एक समान गति से धीमे घुमाते हुए तीव्र प्रकाश किरण पहले दर्पण से दूसरे दर्पण की तरफ भेजी, तो प्रकाश किरण इतनी जल्दी वापस आ गई कि अभी भी वही खाँचा सामने मौजूद था। यानी कि दाँतेदार पहिया इतना भी नहीं घूम पाया था कि उसका अगला दाँता लौटती हुई प्रकाश किरण की राह में बाधा बन जाए।
फिर फीज़ो दाँतेदार पहिए को घुमाने की गति बढ़ाते गए, तो ऐसी स्थिति आई जब दूसरे दर्पण से परावर्तित होकर आई प्रकाश किरण की राह में उस खाँचे के बाद का पहला दाँता आ गया जिससे रोशनी की किरण फीज़ो के पास वापस नहीं पहुँच पाई। दाँतेदार पहिए को और ज़्यादा तेज़ी-से घुमाने पर एक स्थिति ऐसी बनी, कि जब दूसरी पहाड़ी से लौटकर प्रकाश किरण आई, तब तक दाँतेदार पहिए का दूसरा खाँचा सरककर सामने आ गया जिसमें से होकर परावर्तित किरण प्रेक्षक के पास वापस लौट आई।
यदि दाँतेदार पहिया स्थिर है तो पहिए के दाँतों के बीच के रिक्त स्थान में से परावर्तित होकर लौटकर आई किरण की वजह से प्रकाश स्रोत का प्रतिबिम्ब दिखाई देता है। इस प्रयोग के लिए फीज़ो ने अर्धपॉलिश प्लेट एवं उत्तल लेंसों का इस्तेमाल करते हुए सुनिश्चित किया कि प्रकाश किरणों को ज़रूरत के अनुसार फोकस किया जाए एवं लम्बी दूरी तय करने के लिए समानान्तर बना दिया जाए। फीज़ो ने इस दाँतेदार पहिए को जब एक समान गति से घुमाना शुरू किया तो उसने पाया कि जितने समय में प्रकाश पहिए से दूसरे दर्पण तक जाकर पुनः पहिए तक वापस आता है, उतने समय में रिक्त स्थान की जगह दाँतेदार पहिए का निकटवर्ती दाँत सामने आ जाता है। इस स्थिति में प्रकाश स्रोत का प्रतिबिम्ब नहीं दिखता जिसे फीज़ो ने प्रथम ग्रहण कहा। फीज़ो ने पहिए की गति को जब दुगुना किया तो उसने देखा कि प्रकाश स्रोत का प्रतिबिम्ब फिर से दिखने लगा। पहिए की गति को तिगुना करने पर प्रतिबिम्ब दिखना बन्द हो गया, और फीज़ो ने इसे द्वितीय ग्रहण की स्थिति कहा। पहिए की गति को चार गुना करने पर फिर प्रतिबिम्ब दिखने लगा। फीज़ो लगातार पहिए की गति बढ़ाकर घुमाते रहे और देखते रहे कि कब प्रकाश स्रोत का प्रतिबिम्ब दिखता है और कब दिखना बन्द हो जाता है।
इस सबके आधार पर फीज़ो ने प्रकाश की गति की गणना का तरीका निकाल लिया। पहिए की गति मालूम थी, एक खाँचे से दूसरे खाँचे तक पहुँचने में लगने वाला समय भी मालूम था। और प्रकाश किरणों ने कितनी दूरी तय की, यह भी स्पष्ट था। बस इन्हीं आँकड़ों का उपयोग करते हुए फीज़ो ने प्रकाश की चाल ज्ञात की। आइए, समझते हैं कि उन्होंने यह गणना कैसे की।
दूरी के लिए फीज़ो ने दर्पण और दाँतेदार पहिए के बीच की दूरी (d) को दुगुना करके लिया क्योंकि प्रकाश स्रोत से निकलकर पहिए से दर्पण और फिर वापस स्रोत तक लौटता है, अर्थात् दोगुनी दूरी (2d) तय करता है। इस दौरान लगने वाला समय इस बात पर निर्भर करेगा कि दाँतेदार पहिए की कुल परिधि में कितने भाग हैं और एक सेकण्ड में परिभ्रमण के दौरान पहिए के कितने भाग हटेंगे। दाँतेदार पहिए में जितने दाँतों की संख्या होगी उतने ही रिक्त स्थान यानी खाँचे होंगे। यदि दाँतों या रिक्त स्थान की संख्या को हम m से दर्शाएँ तो उस पहिए पर कुल भाग 2m होंगे। ऐसे ही एक सेकण्ड में पहिए के घूमने यानी परिक्रमण की संख्या n हो तो एक सेकण्ड में हटने वाले भागों की संख्या 2mn होगी। इस तरह एक भाग के हटने में लगने वाला समय 1/2mn होगा। फीज़ो ने चाल का सूत्र लगाकर प्रकाश ने जितनी दूरी तय की (2d), उसे लगने वाले समय (1/2mn) से भाग देकर यह बताया कि प्रकाश की चाल 4mnd होगी। यदि ग्रहण की स्थिति हो तो पहले ग्रहण, तीसरे ग्रहण, अर्थात् विषमगुणज वाले ग्रहण के लिए यह 4mnd/(2r-1) हो जाएगा जहाँ r यह इंगित करता है कि ग्रहण कौन-सा है। प्रथम ग्रहण के लिए r का मान 1 व तीसरे ग्रहण के लिए 3 होगा। वहीं यदि ग्रहण की स्थिति समगुणज जैसे द्वितीय या चतुर्थ ग्रहण की स्थिति हो तो प्रकाश की चाल 4mnd/2r के बराबर होगी।
फीज़ो ने इस प्रयोग को 28 बार दोहराया और इस प्रयोग से प्रकाश की गति लगभग 1,96,000 मील या 3,13,300 कि.मी. प्रति सेकण्ड निकली (आधुनिक मान से तकरीबन 13 हज़ार कि.मी. प्रति सेकण्ड ज़्यादा)। इस कार्य के दौरान फीज़ो ही पहले व्यक्ति थे जिन्होंने प्रकाश की तरंग लम्बाई को मापन के स्टैंडर्ड में शामिल करने की वकालत की और प्रकाश की गति नापने के तरीके को अन्तरिक्ष से पृथ्वी पर लाने वाले पहले व्यक्ति भी बने। पेरिस से प्रकाशित होने वाली एक अन्तर्राष्ट्रीय शोध पत्रिका में फीज़ो ने अपने काम को प्रकाशित भी किया। उनके इस प्रयास को इतना सराहा गया कि फीज़ो का नाम 71 वैज्ञानिकों और इंजीनियरों के साथ एफिल टॉवर पर लिखा गया और रोचक बात यह है कि 1889 में विश्व मेले के अवसर पर जब एफिल टॉवर सामान्य जन के लिए खोला गया तो 72 में से केवल फीज़ो ही थे जो उस समय जीवित थे।
सन् 1856 में प्रकाश की गति को दर्शाने के लिए जर्मन वैज्ञानिक रुडोल्फ कोलरौश्च (Rudolf Kohlrausch) और वेबर (Wilhelm Weber) ने ‘c’ संकेत का इस्तेमाल किया जो एक अखबार में पहली बार छपा। इस तरह प्रकाश की गति को एक प्रतीक भी मिल गया।
लेकिन फीज़ो द्वारा पेश की गई विधि में कुछ व्यवहारिक समस्याएँ थीं। मसलन, इस प्रयोग के लिए काफी बड़ी जगह ज़रूरी थी। साथ ही, पहिए को एक समान रफ्तार से घुमाना थोड़ा कठिन था। पहिए और दर्पण के बीच की दूरी बहुत ज़्यादा हो जाने के कारण प्रतिबिम्ब स्पष्ट नहीं दिखता था। उपकरण की सीमाओं को देखते हुए फीज़ो इस विधि से प्रकाश की गति को हवा के अलावा किसी और माध्यम में नहीं निकाल पा रहे थे।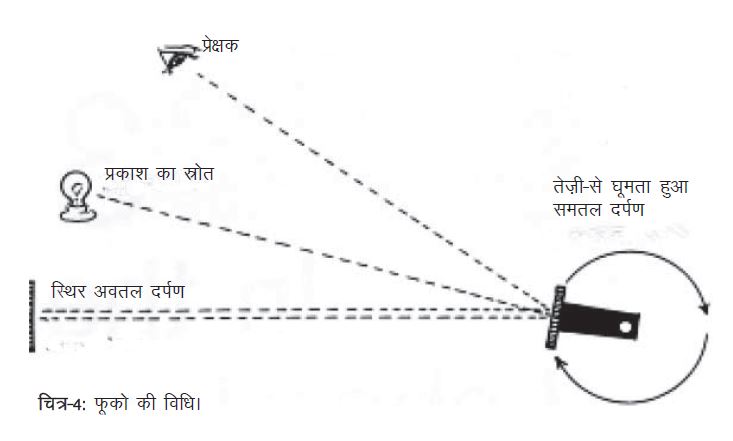 
फूको का तरीका
फ्रांस के ही भौतिक शास्त्री फूको (Jean Leon Focault 1819-68) जो फीज़ो के अच्छे मित्र थे, पृथ्वी की गतियों का अध्ययन कर रहे थे। फूको ने धरती की अक्षीय गति को दिखाने के लिए एक लम्बे तार से बँधे पेंडुलम का उपयोग किया था, जो प्रयोग बाद में दुनियाभर में फूको पेंडुलम के नाम से जाना जाने लगा। यूँ तो फूको ने मेडिकल की पढ़ाई की थी किन्तु सर्जरी का काम इन्हें नहीं भाया, तो इन्होंने आगे भौतिकी में काम करना तय किया। 1849 में प्रकाशित प्रकाश की गति सम्बन्धी शोध पत्र पढ़कर फीज़ो के इस दोस्त ने उसके प्रयोग के दौरान आई चुनौतियों को हल करने की ठानी। इसके लिए फूको ने सारी चुनौतियों का गौर से अध्ययन किया, समझा तथा उन्हें सुलटाने के क्या उपाय हो सकते हैं, इस पर काम शुरू किया।
फूको ने सबसे पहले फीज़ो की तुलना में छोटा अवतल दर्पण लिया। चूँकि फीज़ो द्वारा उपयोग किए गए दाँतेदार पहिए में प्रतिबिम्ब धुँधला दिखता था, तो उन्होंने पहिए का विचार ही त्याग दिया और उसके बदले समतल दर्पण को घुमाने का सोचा जो कि आसानी-से स्थिर गति से घूम सकता है।
फूको के प्रयोग में दर्पण तेज़ी-से घुमाया जा रहा था। जब तक प्रकाश की किरण पहले दर्पण से टकराकर दूसरे दर्पण पर पड़ेगी, तब तक वह अपनी पहले वाली स्थिति से थोड़ा हट चुका होगा और इसलिए अब प्रकाश की किरण पर्दे पर दूसरे स्थान पर पड़ेगी। इस तरह अगर हमें दर्पण के घूमने की गति मालूम हो और यह भी मालूम हो कि प्रकाश की किरण पर्दे पर अपनी पहले वाली स्थिति से कितनी हटती है, तो प्रकाश की गति का पता लगाया जा सकता है।
फूको के उपकरण में एक तीव्र प्रकाश स्रोत से उत्सर्जित किरणें समतल दर्पण पर आपतित होती हैं और परावर्तन के पश्चात् अवतल दर्पण पर पड़ती हैं। समतल दर्पण और अवतल दर्पण के बीच की दूरी, अवतल दर्पण की वक्रता त्रिज्या के बराबर रखी गई थी जिसके कारण किरणें अवतल दर्पण पर पड़ती थीं और परावर्तित होकर उसी मार्ग में वापस लौट जाती थीं। इस प्रकार किरणों द्वारा तय की गई दूरी अवतल दर्पण की वक्रता त्रिज्या (R) की दोगुनी अर्थात् 2R होगी।
समतल दर्पण को जब स्थिर रखा गया तो प्रकाश स्रोत का प्रतिबिम्ब वहीं बनता था जहाँ से प्रकाश किरण आई थी, परन्तु इसे तेज़ी-से घुमाने पर जब तक प्रकाश किरण अवतल दर्पण तक होकर वापस आती, इस घूम रहे समतल दर्पण की स्थिति थोड़ी बदल जाती थी जिससे प्रतिबिम्ब की स्थिति भी बदल जाती थी। यदि समतल दर्पण के प्रति सेकण्ड घूमने यानी परिक्रमण की संख्या n हो तो प्रकाशीय किरण को समतल दर्पण से अवतल दर्पण तक जाने और पुनः समतल दर्पण तक पहुँचने में लगने वाला समय कैसे निकलेगा? एक बार घूमने यानी एक परिक्रमण के दौरान दर्पण द्वारा घूमा गया कोण लगभग 360 डिग्री (यानी 2π रेडियन) होता है। अर्थात् एक सेकण्ड में n परिक्रमण के दौरान समतल दर्पण कुल मिलाकर दोनों के गुणनफल के बराबर अर्थात् 2πn रेडियन के बराबर कोण घूमेगा। तो समतल दर्पण यदि एक निश्चित कोण θ रेडियन से घूमता है तो इतना कोण घूमने में लगने वाला समय θ/2πn के बराबर होगा। ऐसे में दूरी और समय ज्ञात हो जाने पर प्रकाश की चाल का पता लगाया जा सकता है। θ का मान ज्ञात करने के लिए, फूको ने लेंस से दर्पण की दूरी और लेंस से प्रकाश स्रोत की दूरी को भी ध्यान में रखा, जो उसने अपने प्रयोग में 5 मीटर रखी थी। दर्पण को घुमाने के दौरान जो प्रतिबिम्ब विस्थापन हुआ, वह लगभग 0.7 मि.मी. था।
फूको ने अपने दर्पण को एक सेकण्ड में 433 बार घुमाया और ऐसा अवतल दर्पण चुना जिसकी वक्रता त्रिज्या 20 मीटर थी।
फूको की इस विधि से प्रकाश की गति लगभग 1,85,000 मील या 2,98,000 कि.मी. प्रति सेकण्ड प्राप्त हुई। यह गति आधुनिक मान के काफी करीब है।
फूको ने फीज़ो के प्रयोग के लगभग 12 वर्ष बाद 1862 में, कम समय में, कम जगह में, सुगमतापूर्वक प्रकाश की गति ज्ञात की। इसे आसानी-से एक प्रयोगशाला में भी किया जा सकता था। फूको के प्रयोग की खास बात यह रही कि समतल दर्पण और अवतल दर्पण के बीच वायु के अलावा अन्य माध्यम रखकर विभिन्न माध्यम में भी प्रकाश की गति ज्ञात की जा सकती है।
फूको ने पानी में प्रकाश की गति पता करने के प्रयोग भी किए और पाया कि पानी में प्रकाश की चाल हवा की तुलना में कम थी। पानी में प्रकाश की गति 1,40,000 मील प्रति सेकण्ड थी। साथ ही, फूको ने अपने प्रयोग से पता किया कि विरल माध्यम में प्रकाश की चाल अधिक तथा सघन माध्यम में कम होती है। इसे इस उदाहरण से समझें कि हवा में प्रकाश का वेग लगभग 1,85,000 मील प्रति सेकण्ड था जबकि काँच में प्रकाश की गति 1,25,000 मील प्रति सेकण्ड थी। इस प्रकार फूको के प्रयोग से प्रकाश के तरंग सिद्धान्त को और बल मिला। (यह अलग बात है कि कुछ ही सालों में मामला फिर से पलट गया और यह कशम-कश बहुत समय तक जारी रही।)
लेकिन अभी भी ईथर माध्यम पर शंका बनी रही क्योंकि इस विचार का उत्तर नहीं मिल पा रहा था कि कैसे किसी स्रोत से प्रकाश निकलने पर ईथर में तरंगें उत्पन्न हो जाती हैं और इन्हीं तरंगों द्वारा प्रकाश का संचरण होता है।
तो अगला सवाल उठता है कि प्रकाश की चाल ईथर माध्यम में क्या होगी? ईथर जैसा कोई माध्यम है भी कि नहीं? इसे अगले पड़ाव में पढ़ते हैं।
...जारी
अंजु दास मानिकपुरी: अज़ीम प्रेमजी फाउण्डेशन, रायपुर (छत्तीसगढ़) में विज्ञान शिक्षण सम्बन्धी काम कर रही हैं। इससे पहले वे इन्दौर में रसायन विज्ञान की सहायक प्रोफेसर थीं।
इस लेख के लिए आइज़ेक एसिमोव की पुस्तक हाऊ डिड वी फाइंड आउट अबाउट द स्पीड ऑफ लाइट का सन्दर्भ के रूप में एवं कुछ चित्रों के लिए इस्तेमाल किया गया।