रवि कान्त[Hindi,PDF 153KB]
अध्यापकों (इसमें शिक्षक-शिक्षिकाएँ, दोनों ही शामिल हैं) के साथ ऐसी अवधारणाओं पर काम करना काफी मुश्किल होता है जिस बारे में उनका मानना है कि उन्हें सब कुछ पहले से ही पता है, उसमें नया सीखने को है ही क्या। जो आप पहले से ही जानते हैं उसके प्रति सीखने की रुचि पैदा करना व टिकाए रखना मुश्किल ही है। जैसे घटाव की अवधारणा को ही लीजिए। अब दो अंकों के हासिल के घटाव भला किसको नहीं आते होंगे। लेकिन क्या गणनविधि जान लेना भर ही उस अवधारणा को समझ लेने का पर्याय होता है?
वैसे भी किसी गणना को सटीकता व जल्दी-से कर लेना सिर्फ इस बात का सबूत होता है कि आप उस गणना के सभी कदमों को ठीक से याद रख कर, उनका सही से इस्तेमाल कर पाते हैं।
मानक गणनविधि से घटाव की समस्याओं को हल करना तो स्कूलों में सिखाया जाता है। जो किसी वजह से स्कूल नहीं जा पाए वे भी हासिल के घटाव के सवालों को हल कर ही लेते हैं। और स्कूल जाने वाले भी अक्सर आम ज़िन्दगी में ऐसे सवालों को इकाई दहाई व हासिल की मदद से नहीं बल्कि कुछ अन्य तरीकों से हल करते हैं। ऐसा ही एक तरीका है भरपाई वाला तरीका।
भरपाई वाला तरीका
इसमें, जिस संख्या में से घटाना है यानी वियोज्य और जिस संख्या को घटाया जाना है यानी वियोजक, दोनों को या दोनों में से किसी एक को करीबी दशक में बदलकर सवाल को हल किया जाता है यानी अगर 43 में से 27 घटाना है तो 43 को करीबी दशक 40 में और 27 को करीबी दशक 30 में बदल कर दोनों संख्याओं को आपस में घटाया जाए। इससे दोनों संख्याओं को आपस में घटाना बहुत आसान हो जाता है। लेकिन इस सवाल को आसान बनाने के लिए इसमें सवाल की संख्याओं में जो जोड़ व घटा किए गए हैं, उनकी भरपाई शेषफल के साथ करनी पड़ती है, तभी सही जवाब मिल पाता है। इसी वजह से इसे भरपाई वाला तरीका भी कहते हैं। जोड़ के सवाल में तो यह भरपाई बड़ी आसान-सी होती है, उदाहरण के लिए, 24+17 = ? को आप इस तरह से हल कर सकते हैं, जैसे, 
घटाने में भरपाई
अध्यापकों व अध्यापिकाओं को घटाने का एक सवाल, 32 - 18 = ?, भरपाई के तरीके से हल करने के लिए दिया गया। उनसे यह भी कहा गया कि वे मानक गणनविधि से हल करने की बजाय इस सवाल को भरपाई वाले तरीके से ही हल करें। थोड़ी ही देर में पाँच अलग-अलग तरह से किए गए हल सामने आए, जिनसे तीन तरह के जवाब मिल रहे थे। तो कैसे पता करें कि कौन-सा जवाब सही है? एक अध्यापिका ने इसका आसान-सा तरीका सुझाया कि मानक गणनविधि से जवाब निकालकर देख लें। तो सही जवाब मिला शेषफल 14। हमने सभी जवाबों पर बातचीत कर उनके कारण तलाशने व समझने की कोशिश की लेकिन यहाँ पर मैं अपने लेख को उनमें से सबसे पेचीदा तरीके से हासिल किए गए सही जवाब के गणितीय कारणों की खोजबीन पर ही केन्द्रित रखूँगा।
एक अध्यापिका ने सवाल हल करने के लिए संख्याओं के जोड़ व घटा, दोनों का इस्तेमाल किया था। उनका हल कुछ इस तरह था,
एक अध्यापिका ने तर्क समझाने की कोशिश की। उन्होंने कहा, “जैसे हमने जोड़ के सवाल को भरपाई के तरीके से हल करते वक्त जितनी संख्याओं को सवाल की संख्याओं में जोड़ा था उतनी ही संख्या को योगफल में से घटा दिया तो हमें सही जवाब मिल गया। उसी तरह से हमने इसमें भी किया है।”
एक दूसरी अध्यापिका ने कहा, “वैसा करने पर तो हमें 10 अ 2 - 2 करना पड़ेगा और जवाब 10 मिलेगा, जो कि सही नहीं है।”
“हाँ, यह बात तो सही है,” पहली अध्यापिका को अपने तर्क में खोट नज़र आ गई। समूह में यह बात रखी गई कि इसका मतलब यह हुआ कि हम जोड़ के सवालों को भरपाई के तरीके से हल करते वक्त काम में लिए गए सामान्यीकरण को ज्यों-का-त्यों आँख मूँद कर काम में नहीं ले सकते हैं।
एक अध्यापिका ने और कोशिश की। उन्होंने बताया, “चूँकि हम वियोज्य में से 2 घटा रहे हैं इसलिए शेषफल में 2 को बढ़ा देंगे और वियोजक में 2 बढ़ा रहे हैं, इसलिए शेषफल में फिर से 2 बढ़ा देंगे।”
फिर से एक अन्य अध्यापिका ने ध्यान दिलाया, “आपने तो हल निकालने के तरीके के कदमों का शब्दों में वर्णन कर दिया है, लेकिन आपकी बात में - ऐसा क्यों करेंगे - उसके कारण का पता नहीं चल रहा। हम इस सवाल का जवाब खोज रहे हैं कि जब सवाल में से वियोज्य संख्या को घटाया है और वियोजक संख्या को बढ़ाया है तो जवाब में आए शेषफल में दोनों संख्याओं को जोड़ने से ही सही जवाब क्यों आ रहा है?”
इस समूह में सभी अध्यापिकाएँ 12वीं कक्षा पास करके आगे की पढ़ाई कर रही थीं, उनमें से कोई-कोई तो स्नातक भी थीं। भरपाई की कार्यनीति को काम में लेते ही घटाने का एक सादा-सा सवाल अध्यापिकाओं के लिए चुनौतीपूर्ण बन चुका था। सभी को न सिर्फ सही जवाब के तर्क को सोचकर भाषा में व्यक्त करने का बल्कि अपने जवाब पर साथियों के प्रतिप्रश्न सुनकर पुनर्वचिार करने का मौका भी मिल रहा था। इससे उनके सामने खुद के तर्क की सीमाएँ भी उजागर हो रही थीं। आप यह भी देख सकते हैं कि अध्यापिकाएँ समूह में आए विचारों की आलोचना भी कर रही हैं और उन्हें तर्क के आधार पर स्वीकार भी कर रही हैं।
यहाँ पर आकर बातचीत अटक-सी गई। आगे बढ़ने के लिए समूह के सामने एक सुझाव रखा गया कि बजाय शब्दों में सोचते रहने के, क्यों नहीं इस हल के गणितीय तर्क को समझने के मॉडल की मदद से इस सवाल के तर्क को समझने की कोशिश करें। उन्हें कहा गया कि वे मापन मॉडल में संख्या रेखा पर इस हल को दर्शा कर भरपाई के गणितीय तर्क समझाने की कोशिश करें। सभी के साथ मापन मॉडल पर संख्याओं को दर्शाने के तरीकों व सवालों को हल करने पर पहले काम किया जा चुका था।
सभी कुछ देर तक संख्या रेखा के द्वारा सवाल और उसके हल को दर्शाने व उसके सही होने के तर्क को तलाशने की जद्दोजहद करते रहे लेकिन उन्हें भरपाई वाले तरीके से हल किए गए सवाल को संख्या रेखा पर दर्शाने में मुश्किल पेश आ रही थी। सही तर्क खोजने के दबाव ने कुछ वक्त के लिए हम सभी के दिमागों को कुन्द कर दिया था सो इसे अगले दिन करने के लिए स्थगित कर दिया गया। सभी से कहा गया कि वे इस सवाल के तर्क के बारे में सोचकर आएँ या कुछ करके लाएँ।
अगले दिन ज़्यादातर अध्यापिकाएँ तो इसे करके नहीं लाईं लेकिन गणित में रुचि रखने वाली एक अध्यापिका ने नीचे दिए तरीके से सवाल के हल को दर्शाया (चित्र-1)।
अध्यापिका से पूछा गया कि उसने इसे कैसे हल किया। उन्होंने बताया कि पहले 32 में से 2 कम करके 30 तक पहुँचे। फिर 30 में से 20 घटाना आसान था तो 20 को घटा कर 10 तक पहुँचे। फिर 10 में 2 मिलाकर 12 तक पहुँचे। अब 30 और 12 के बीच की दूरी या फर्क 18 है। अब 10 में 2 और 2 जोड़ दिए तो 14 आ गए और 18 व 14 की लम्बाई को मिलाया तो 32 मिल गए। अध्यापिका तो सवाल को समझाकर सन्तोष के साथ बैठ गई। उसके चेहरे पर संख्या रेखा पर सवाल को हल कर पाने की आभा थी।
हम सभी कुछ पलों के लिए खामोश हो गए। जवाब दिख तो रहा था लेकिन इस हल में कोई बात थी जो खटक रही थी। सभी संख्याएँ या तो संख्या रेखा पर थीं या दो संख्याओं के फर्क के तौर पर नज़र आ रही थीं। जवाब दिख भी रहा था और समझ भी नहीं आ रहा था। कुछ देर के सन्नाटे के बाद सवाल पर सोचने की शुरुआत करने के लिए समूह से व खुद से यह सवाल पूछा गया कि इस प्रस्तुतिकरण में क्या चीज़ है जो समझ में नहीं आ रही या यह उलझा-पुलझा क्यों लग रहा है।
थोड़ा गौर से सवाल के प्रस्तुतिकरण को देखने पर यह समझ आया कि इसमें संख्या रेखा पर वियोज्य संख्या 32 तो दर्शाई गई है लेकिन वियोजक संख्या 18, संख्या रेखा पर नज़र नहीं आ रही थी। यह साफ था कि अध्यापिका ने पहले 32 में से 2 घटाकर 30 हासिल कर लेने को तो ठीक से संख्या रेखा पर दर्शा दिया था लेकिन उसके बाद अध्यापिका ने 18 को दर्शाने की बजाय 30 में से 20 घटाने पर मिले 10 को संख्या रेखा पर दर्शा कर सवाल को आगे हल करना आरम्भ कर दिया था। यानी आंशिक शेषफल को सवाल में आए वियोजक की जगह लेकर संख्या रेखा पर दिखा दिया गया था और शेषफल भी तीन टुकड़ों : 10, 2 व 2 में संख्या रेखा पर दिखाई दे रहा था, जबकि उसे संख्या रेखा पर दर्शाई गई संख्याओं के बीच फर्क के तौर पर नज़र आना था।
बाद में सोचने पर लगा कि इस प्रस्तुतिकरण की समस्या को सभी के सामने उजागर करने का एक तरीका यह भी हो सकता था कि सभी को यह कहा जाता कि वे इस प्रस्तुतिकरण का फिर से अंक व अन्य प्रतीकों की मदद से गणितीय निरूपण करके देखें। यानी दृश्यात्मक प्रस्तुतिकरण को फिर से सवाल में बदल कर देखें। यह भी एक अच्छी कार्यनीति है। क्या वह सवाल हमें उसी प्रारूप में फिर से मिलता है जिसे आपने संख्या रेखा पर दर्शाया है? जैसे इस संख्या रेखा पर दर्शाए गए सवाल को लिखा जाए तो वह कुछ इस तरह से होगा,
साफ है कि ये तो हमारे सवाल का प्रारूप न था। यानी संख्या रेखा पर दर्शाते वक्त अध्यापिका को पता ही न चला और सवाल का प्रारूप ही बदल गया।
आप देख सकते हैं कि भरपाई वाले तरीके को किसी मॉडल के ज़रिए प्रस्तुत करने का तरीका शिक्षकों के सामने चुनौती पेश करता है। भरपाई वाले तरीके की पेचीदगी और उसे संख्या रेखा पर दर्शाते वक्त अध्यापिका के सोचने के तरीके की उलझनें आपके सामने एक चुनौती पेश करती हैं कि आप व पूरा समूह उसी वक्त सोचकर उन उलझनों को साफ करके फिर से दिखा सकें। यह मौका होता है जब आप सवाल को हल करने वाले के दिमाग में झाँककर यह अनुमान लगा सकते हैं कि वह किन मोड़ों पर सही और किन मोड़ों पर गलत। इसी तरह हल करने वाले के लिए यह मौका होता है कि उलझनों की पहचान कैसे की जाए, यानी अध्यापक-शिक्षक के सोचने की प्रक्रिया को समझने का। ऐसा मौका मानक गणनविधि से सवालों को हल करते वक्त न तो सिखाने वाले और न ही सीखने वाले को मिलता है।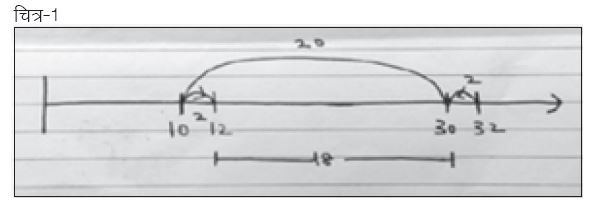

जैसे, हम सवाल का जवाब न् मान लेते हैं, तो हमारा सवाल बन गया, 32-18 + x
जब हमने इस समीकरण के बाएँ बाजू में कुछ बदलाव किए तो समीकरण में सन्तुलन के लिए वैसे ही बदलाव दाएँ बाजू में भी करने पड़ेंगे। पहले हम देखते हैं कि हमने बाईं बाजू में क्या बदलाव किए,
32-2 और 18+2 यानी समीकरण के बाएँ हिस्से में रखें तो ऐसा होगा,
(32 - 2) - (18 + 2)
अब हम यह जानना चाहते हैं कि हमने बाँई बाजू में वास्तव में क्या जोड़ा व घटाया तो हम दोनों कोष्ठक हटा कर दोनों संख्याओं को अलग करके देखते हैं,
32 - 18 + (- 2) - (+ 2)
यानी समीकरण को बराबर रखने के लिए हमें (-2) - (+2) को समीकरण के दूसरे बाजू में भी जोड़ना पड़ेगा। अब हम इसे करके देखते हैं,
32 - 18 + (-2) - (+2)
= x + (-2) - (+2)
या, (32-2) - (18+2) = x - 2 - 2
या, 30-20 = x - 2 - 2
या, 10 = x - 2 - 2
या, 10 + 2 + 2= x
यानी इस समीकरण से भी हम देख सकते हैं कि अगर हम सवाल के बाईं बाजू में ली गई दो संख्याओं में अन्य दो संख्याओं का घटा व जोड़ करते हैं तो हमें उसकी भरपाई के लिए दाईं बाजू में भी उन दोनों संख्याओं को जोड़ना पड़ेगा।
इसे इस तरह से भी समझा जा सकता है कि हमें जिस संख्या में से घटाना था यानी वियोज्य, उसे हमने 2 से कम कर दिया तो शेषफल को हमें 2 से बढ़ाना पड़ेगा। लेकिन हमें घटाना 18 था और हमने उसमें 2 बढ़ाकर यानी 20 घटा दिया। यानी हमें छोटी संख्या 18 घटानी थी लेकिन हमने उससे बड़ी 20 संख्या घटा दी यानी हमने 2 ज़्यादा घटा दिए और हमने शेषफल को 2 से कम कर दिया तो हमें फिर से शेषफल को 2 से बढ़ाना पड़ेगा। यह भाषा थोड़ी मुश्किल-सी लग सकती है क्योंकि हम गणित में भाषा की मदद से सोचने के आदी नहीं हैं। हमें भी यहाँ तक पहुँचने के लिए संख्या रेखा व समीकरण बना कर इस समस्या को समझना पड़ा और साथियों के साथ मिलकर सोचना पड़ा तब कहीं जाकर इस भाषा में तर्क को रखा जा सका। 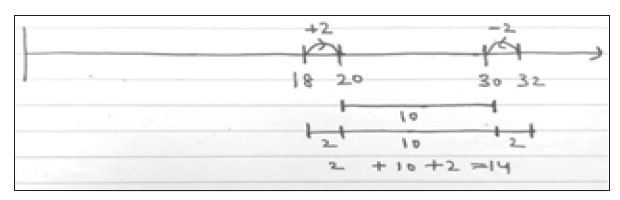
रवि कान्त: शैक्षिक सलाहकार के तौर पर विभिन्न संस्थाओं, अध्यापकों के साथ काम। शिक्षण सामग्री, पाठ्यपुस्तकों, प्रशिक्षण सन्दर्शिकाओं आदि का निर्माण, शैक्षिक शोध और अनुवाद। गणित शिक्षण में विशेष रुचि।

