ईरेटोस्थीनस की छलनी

लेखक :   जिल ब्रिटॉन
अनुवाद :  मनोज जैन

कोई भी प्राकृत संख्या जो केवल दो धनात्मक संख्याओं, 1 और वह संख्या खुद से भाज्य हो तो उसे अभाज्य संख्या (प्राइम नम्बर) कहते हैं। यदि ऐसा नहीं है तो वह संख्या भाज्य संख्या है। संख्या 1 को सामान्यत: न तो भाज्य, न ही अभाज्य संख्या माना जाता है।
सायरीन के ईरेटोस्थीनस (276 से 194 ईसा पूर्व) वह पहले व्यक्ति थे जिन्होंने पृथ्वी की परिधि का सही अनुमान लगाया था। कई दशकों तक वे अलेक्ज़ेण्ड्रिया के प्रसिद्ध ग्रन्थालय के निदेशक पद पर कार्यरत रहे। अपने समय में उन्हें बहुत सम्मान प्राप्त हुआ। ईरेटोस्थीनस ने जियोग्राफिया नामक ग्रन्थ लिखा था। दुर्भाग्य से उनकी कोई भी मूल रचना नहीं मिली। उनकी रचनाओं के बारे में बाद के लेखकों ने अपनी किताबों में ज़रूर ज़िक्र किया।

ईरेटोस्थीनस ने अविभाज्य संख्याओं का पता लगाने के लिए एक छलनी तैयार की, इसे छलनी इसलिए कहा गया क्योंकि यह पाककला में इस्तेमाल होने वाली छलनी जैसा ही काम करती है। आपने भी घर में ओसना चावल पकाते समय चावल की देगची को टोकरी में उड़ेलकर पानी को अलग निकाला होगा। ईरेटोस्थीनस की छलनी भाज्य संख्याओं को छानकर अलग कर देती है जिससे फिर अभाज्य संख्याएँ बच जाती हैं। ईरेटोस्थीनस का भाज्य संख्यायों को छानने का तरीका इस तरह से था।
मान लीजिए आप कोई संख्या द तक की संख्याओं में से अभाज्य संख्याओं को पहचानना चाहते हैं तो आपको निम्न कदम उठाने होंगे।
--- सभी ऐसी पूर्णांक संख्याओं की सूची बनाएँ जो कि एक से बड़ी हों और द से छोटी या तुल्य हों।
--- अब उन सभी अभाज्य संख्याओं (जो कि द के वर्गमूल से छोटी या तुल्य हों) के गुणांकों को काट दें।
--- इसके बाद जो संख्याएँ शेष रहेंगी वे अभाज्य संख्याएँ होंगी।
ध्यान दीजिए कि यदि एक विभाजक या किसी संख्या का एक गुणनखण्ड, (संख्या के पूर्ण वर्ग के अलावा) इसके वर्ग मूल से बड़ा हो, तब दूसरा घटक इसके वर्ग मूल से छोटा होगा। इसलिए उन अभाज्य संख्याओं के गुणांक निकालने की ज़रूरत नहीं है जो अभाज्य संख्याएँ द के वर्ग मूल से बड़ी हैं।
उदाहरण के लिए 50 से छोटी सभी अभाज्य संख्याओं को ज्ञात करने के लिए पहले हम 2 से 50 तक संख्याओं की सूची बनाएँगे।

पहली अभाज्य संख्या 2 है, सो इसे रखकर इसके गुणांकों को काट दें। यहाँ काले चौकोरों में दिए गए अंक 2 के गुणज हैं।

अब शेष संख्याओं में अगली संख्या 3 है, यह पहली विषम अभाज्य संख्या है। इसे रखें और इसके सभी गुणंाकों को काट दें। 6 और 12 के समान वे सभी संख्याएँ जो कि 2 की गुणांक हैं पूर्व में ही काटी जा चुकी हैं।

शेष बची अगली संख्या है 5, यह दूसरी विषम अभाज्य संख्या है। अत: इसे रखें और इसके सभी गुणांकों को काट दें, 25 और 35 ही केवल वे संख्याएँ हैं जो कि अब तक काटी नहीं गई हैं।

अगली संख्या जो शेष है, वह है 7, तीसरी विषम संख्या। अत: इसे रखें और इसके सभी गुणांकों को काट दें। 49 ही वह संंख्या है जो अब तक काटी नहीं गई है।

अगली शेष संख्या 11 है, यह 50 के वर्गमूल से बड़ी है, अत: शेष सभी संख्याएँ अभाज्य संख्याएँ हैं। क्या आप सोच सकते हैं कि ऐसा क्यों है?
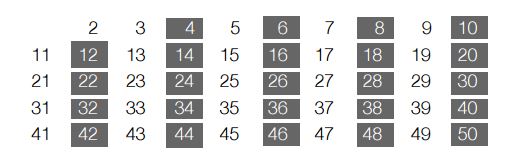
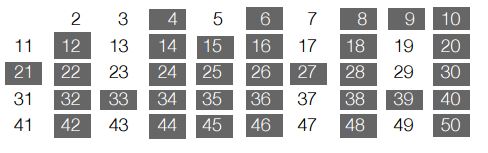
जैसा कि ऊपर दर्शाया गया है 50 से छोटी अभाज्य संख्याएँ हैं 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47। ध्यान दें कि हमने बिना भाग दिए इन अभाज्य संख्याओं को प्राप्त किया है।

जिल ब्रिटॉन: शिक्षक, कंसलटेंट, लेखक, गणित शिक्षण में गहरी रुचि। कैमोसन कॉलेज विक्टोरिया, ब्रिटिश कोलम्बिआ, कनाडा में गणित पढ़ाती हैं। प्राथमिक शिक्षा के विद्यार्थियों और शिक्षकों के लिए कार्यशालाओं का आयोजन करती हैं।

अँग्रेज़ी से अनुवाद - मनोज जैन - वर्तमान में ज़िला संसाधन केन्द्र, हरदा में व्याख्याता हैं। गणित और अँग्रेज़ी में स्नातकोत्तर और एम.एड. किया है। सम्पादन, अनुवाद और फोटोग्राफी में रुचि।

यह लेख जिल ब्रिटॉन के होम पेज से साभार। मूल लेख के लिए वेब साइट देखिए -
http://britton.disted.camosun.bc.ca/jberatosthenes.htm

यदि आप ईरेटोस्थीनस की छलनी से संख्याएँ छानना चाहते हैं तो
http://britton.disted.camosun.bc.ca/sieve/jberatosapplet.htm साइट पर क्लिक करें।