गणक से गणित की समझ

विजय शंकर वर्मा

लोग मानते हैं कि संख्याएं और गणितीय क्रियाएं के मामले में बच्चों की प्रगति ठोस से सांकेतिक और फिर अमूर्त की ओर होनी चाहिए यानी शुरूआत सेव, संतरे, टॉफियां जैसी ठोस वस्तुओं से, फिर धीरे-धीरे इनके बदले कंकड़, पत्थर आदि का उपयोग और इसके बाद कहीं जाकर बच्चों को कागज़ पर चित्र बनाकर लिखे संकेतों से मिलान करना सिखाना चाहिए। इनमें से सांकेतिक पक्ष के समय गणक (एबेकस) काफी मददगार साबित हो सकता है। क्योंकि इस पर बच्चा सिर्फ मोतियों को ही नहीं खिसकाता बल्कि अंकों को महसूस करता है।

हममें से शायद सब गणक (एबेकस) के बारे में जानते होंगे। लेकिन अगर याद करने बैठें तो शायद बड़ी मुश्किल होगी यह सोच पाने में कि वो कैसा होता है या उससे क्या-क्या किया जा सकता है।

लेकिन दुनिया के कई दूसरे देशों में यह खासा प्रचलित है। इसके इस्तेमाल में लोग इतने दक्ष हैं कि तेजी से गणनाएं करने के मामले में कई यंत्रों को भी चुनौती दे डालते हैं। बस करेंगे और साथ-साथ अपने लिए एक बनाएंगे भी।

एबेकस (गणक) में एक चौकोर ढांचा होता है, जिसमें एक-दूसरे के समान्तर लगी तोरों में मोती फंसे होते हैं। गणनाएं करने में इससे फायदा इसलिए होता है क्योंकि इन मोतियों पर संख्याओं को दर्शाया जा सकता है। अगर इसमें दक्ष हो जाएं तो जोड़, घटा, गुणा भाग बड़ी आसानी और फुर्ती से किए जा सकते हैं।

अनुमान है कि करीब पांच हजार साल पहले बेबिलोन में इसका आविष्कार हुआ। एशिया (भारत को छोड़कर) में प्रचलित हो गया। इसको इस्तेमाल करना इतना आसान और सरल था तथा गणनाओं के नतीजे इतने सही आते थे कि बहुत तेज़ी से यह व्यापक प्रचलन में आ गया। संभव है कि इसके व्यापक प्रचलन का उन इलाकों के लोगों में लिखित संख्याओं के विकास पर प्रभाव पड़ा हो - लिखित प्रस्तुतिकरण के तरीके कमज़ोर रह गए हों। यह भी तर्क दिया जा सकता है कि शून्य और स्थानीय मान की अवधारणा समेत दशांक पद्धति का विकास भारत में इसीलिए हो सकता क्योंकि यहां एबेकस कभी प्रचलित नहीं रहा। दरअसल अरबों द्वारा 17वीं शताब्दी में यूरोप को दशांक पद्धति से परिचित कराने के बाद धीरे-धीरे इस नई पद्धति ने एबेकस को स्थानांतरित को लिख कर स्थायी बनाया जा सकता था और साथ ही आंकड़ों का इस्तेमाल सरल भी था। लेकिन मध्यपूर्व, रूस, चीन और जापान में आज भी लोग गणनाएं करने के लिए एबेकस इस्तेमाल करते हैं क्योंकि बचपन से ही इसका प्रशिक्षण मिलने के कारण कुछ लोग इसके इस्तेमाल में इतने दक्ष हो जाते हैं कि तेज़ी के मामले में तो वे गणना करने वाले अन्य यंत्रों को भी चुनौती दे पाते हैं।

चीन में अधिकतर दुकानदार गणनाएं करने के लिए दोनों साधन रखते हैं - एबेकस भी और कैलकुलेटर भी। एबेकस इसलिए ताकि वे खुद तेज़ी से गणनाएं कर लें और कैलकुलेटर इसलिए ताकि बाहर से आने वालों को गणना कर संतुष्ट कर सकें कि वे उनसे सही पैसे ले रहे हैं! लेकिन कुल मिलाकर यह स्थिति बन रही है कि लगातार सस्ते होते जा रहे कैलकुलेटर धीरे-धीरे एबेकस का स्थान लेते जा रहे हैं।

गणित सीखने के कदम   
परन्तु एक फर्क दृश्य भी दिख रहा है। एक तरफ तो उन देशों से एबेकस गायब होता जा रहा है जहां पहले कभी बहुत प्रचलित था। वहीं आस्ट्रेलिया जैसे देश में बच्चों को प्रेरित किया जा रहा है कि एबेकस सिखाने वाली विशेष कक्षाओं में जाएं और उसके इस्तेमाल में दक्ष हों। आखिर ऐसा क्यों?

दरअसल कई लोग मानते हैं कि संख्याएं और गणितीय क्रियाएं सीखने के मामले में बच्चों की प्रगति ठोस से सांकेतिक और फिर अमूर्त (abstract) की ओर होनी चाहिए। वैसे ये भी एक अमूर्त वाक्या लगता है। चलिए इसे समझते हैं। जैसे जोड़, घटा आदि क्रियाओं को सीखने के लिए शुरूआत में ठोस वस्तुओं जैसे सेव, संतरे, टॉफियां आदि का इस्तेमाल होना चाहिए। फिर धीरे-धीरे इनके बदले कंकड़, पत्थर, गुटकों को इनके प्रतीकों के रूप में इस्तेमाल करना चाहिए। इसके बाद बच्चों को कागज़ पर चित्र बनाकर लिख संकेतों से मिलान करना सिखाना चाहिए। इन सभी कदमों के बाद ही बच्चों को वास्तविक रूप में अंको से परिचित कराना उचित होगा। शायद इन्हीं रास्तों से होकर ही बच्चों में गणितीय सिद्धांतों की समझ का सही विकास हो सकता है और वे उन्हें आत्मसात कर पाते हैं।

यदि कोई सीखने के इन तरीकों पर विश्वास करता है तो एबेकस बच्चे में अंकों से संबंधित क्रियाओं से जुड़ी क्षमता के विकास में काफी मददगार साबित हो सकता है। एबेकस सांकेतिक रूप में अंकों की पहचान का एक ठोस उदाहरण है जो बच्चों में हस्तकौशल विकसित करने में भी सहायक होता है। एक तरह से बच्चा इसमें अंकों को महसूस करने की दक्षता बच्चा इसकी सहायता से विकसित कर सकता है। इन सभी कारणों कसे ऑस्ट्रेलिया जैसे देश में माता-पिता बच्चों को एबेकस सीखने के लिए प्रेरित कर रहे हैं।

चलिए इस बहस को यहीं छोड़कर वहीं से शुरूआत करते हैं जहां बात छोड़ी थी - एबेकस में एक चौकोर फ्रेम पर समानान्तर तारें लगी होती हैं जिनमें मोती फंसे रहते हैं। लेकिन दुनिया के अलग-अलग होते हैं। यानी एबेकस को देखकर यह बताया जा सकता है कि वो दुनिया के किस हिस्से से आया है। जैसे रोमन गणक में हर तार में 10 मोती होते हैं और हर मोती का मान एक इकाई होता है। वहीं चीनी जापानी एबेकस में खड़ी तारें तो वैसी ही रहती हैं  लेकिन वे बीच मे एक लंबवत पट्टी से ऊपर और नीचे के हिस्सों में बंटी होती हैं। चीनी गणक में ऊपर वाली तारों में दो-दो मोती और नीचे के हिस्से में पांच-पांच मोती होते हैं। वहीं जापानी गणक में ऊपर एक-एक मोती और नीचे के हिस्से में चार-चार मोती होते हैं। मोतियों का मान दोनों में एक-सा होता है। ऊपर के मोतियों का मान 5 इकाई के बराबर और नीचे के मोतियों का मान एक इकाई होता है। मोतियों की संख्या चाहे कुछ भी हो गणना करने के मूल सिद्धांत तीनों में से एक होते हैं।

अब हम यहां जिस गणक की चर्चा करेंगे वह रोमन गणक का एक थोड़ा-सा बदला रूप है। इसमें हर तार में 9 मोती फंसे रहते हैं। चलिए, हम गए गणक बनाते हैं और साथ ही यह भी देखते हैं कि गुणा, भाग, जोड़, घटा की क्रियाएं इसमें कैसे की जाती हैं।

अपना गणक बनाएं:
हमें ज़रूरत है एक चौकोर मोटे गत्ते के डिब्बे की, जूते का डिब्बा भी चलेगा। साथ ही यह सब सामान भी चाहिए होगा - 81 बड़े मोती या मोटे किस्म के बटन, लगभग दो मीटर मोटा धागा और मोटी सुई।

सुई में धागा पिरोकर उसमें नीचे की तरफ गांठ लगा दीजिए। चित्र में दिखाए अनुसार सुई से गत्ते के एक तरफ छेद कर दूसरी तरफ निकाल लीजिए। अब नौ मोतियों को धागे में पिरो दीजिए। और फिर दूसरी तरफ सुई से गत्ते को छेद कर धागे को बाहर निकाल लीजिए। ये तैयार हो गई आपकी पहली तार। इसी तरह थोड़ी-थोड़ी दूरी रखकर आठ लाइनें और बना लीजिए; और ये तैयार हो गया आपका गणक।

किस मोती का क्या मान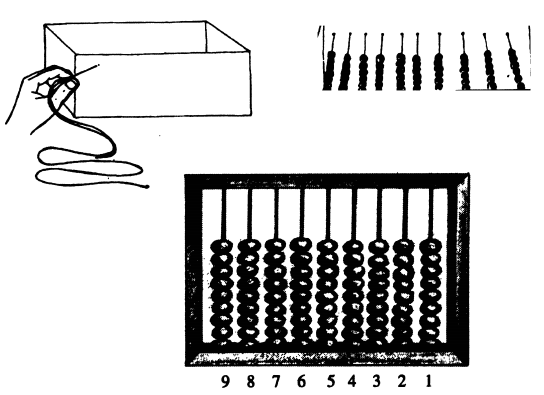  
दाहिनी ओर तोर से शुरू करते हैं। पहली तार के हर मोती का मान एक इकाई है। दूसरी तार के हर मोती का मान 10 इकाई के बराबर है। इसी तरह तीसरी तार के मोती 100 इकाई के बराबर हैं। ऐसे ही आगे बढ़ते रहें तो नौवीं तार के मोती का मान 10 करोड़ इकाई के बराबर होगा। नियम है कि किसी भी तार के मोती का मान उसके दाहिनी ओर के तार के मोती के मान का दस गुना और बार्इं ओर के तार के मान का 1/10 होगा।

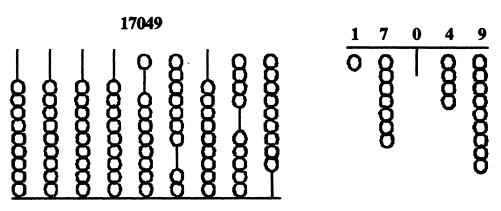
कोई भी गणितीय क्रिया करने से पहले गणक को शून्य पर स्थिर करते हैं। ऐसा करने के लिए सभी तार के  मोतियों को नीचे खिसका देते हैं। अब गणक पर कोई अंक दिखाने के लिए उससे संबंधित तार के मोतियों को ऊपर खिसका देते हैं। जैसे कि 17049 को गणक पर इस तरह से दिखाएंगे। इस संख्या में इकाई का अंक है नौ, तो पहले स्तंभ के 9 मोतियों को ऊपर खिसका दिया। इकाई का अंक है 4 तो दहाई मान वाले मोतियों के स्तंभ के चार मोती ऊपर उठा दिए। इसी तरह आगे बढ़ते हैं।

गणक पर जोड़   
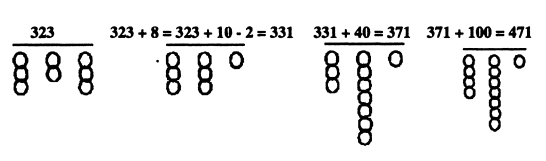
जैसे हमें 323 में 145 को जोड़ना है:              

   323
+ 145

इस जोड़ को करने के लिए हम पहले 323 को गणक पर दिखाते हैं। अब आगे का जोड़ हम क्रम से करेंगे। पहले पांच जोड़ने के लिए इकाई स्तंभ के मोती ऊपर कर दिए। इसी तरह 40 जोड़ने के लिए दहाई के तार से चार मोती ऊपर कर दिए। अंत में 100 जोड़ने के लिए सैंकड़े के तार का एक मोती ऊपर कर दिया। अब ज़रा मोती गिनते हैं कि हमने कितने ऊपर चढ़ाए। सैंकड़े वाले स्तंभ में चार मोती यानी 400, दहाई वाले स्तंभ में 6 मोती यानी 60 और इकाई के स्तंभ में 8 मोती। कुल जोड़ हुआ 46.8 लेकिन ये तो एक सरल-सा जोड़ था।

एक दूसरा जोड़ देखते हैं।

   323
+ 148

शुरुआत इसमें भी उसी तरह से करते हैं - 323 को गणक पर दिखाकर। अब पहले जोड़ना है 8 जिसके लिए आठ मोती ऊपर ले जाने होंगे; लेकिन इकाई के स्तंभ में हमारे पास इतने मोती नहीं है। यह तो हमें मालूम है कि 8 को इस तरह भी लिखा जा सकता है 10 - 2 उ 8; तो  हम गणक के दहाई वाले स्तंभ का एक मोती ऊपर उठा देते हैं और इकाई वाले स्तंभ के दो मोती नीचे। इस तरह हमने 323 में 8 जोड़ दिए। अब जोड़ना है 40; दहाई वाले तार में हमारे पास पर्याप्त मोती हैं, इनमें से चार ऊपर कर दिए। इसी तरह 100 जोड़ने के लिए सैंकड़े वाले तार से एक मोती ऊपर कर दिया। अब देखें कि हमने कितने मोती ऊपर उठाए यानी कुल कितना जोड़ आया। सैंकड़े वाले स्तंभ में चार यानी 400; दहाई वाले में 7 मोती, यानी 70; और इकाई वाले में एक मोती। कुल उत्तर आया 471.

गणक पर घटाना  
गणक पर साधारण घटाना उतना ही आसान है जितना पहले वाला साधारण जोड़ था। उदाहरण के लिए थोड़ी जटिल-सी संख्याएं लेते हैं।

  428
– 145

पहले गणक पर 428 संख्या दिखा दी। अब पहले घटाना है पांच तो इकाई के ऊपर चढ़े 8 मोतियों में से 5 नीचे कर दिए। दूसरे चरण में घटाना है चालीस। अब नीचे करने के लिए चाहिए चार मोती, लेकिन दहाई के स्तंभ में ऊपर हैं सिर्फ दो मोती, तो फिर? इस बार भी कुछ उसी तरह करें जैसे जोड़ में किया था। हमें मालूम है कि 40 को इस तरह भी लिखा जा सकता है 100 - 60 उ 40; इसलिए सैंकड़े के स्तंभ में 1 मोती नीचे उतारा और दहाई के स्तंभ में छह मोती ऊपर चढ़ा दिए। अब तीसरे और अंतिम चरण में घटाना है 100; बस इसे करने के लिए सैंकड़े के तार में ऊपर चढ़े मोतियों में से एक नीचे उतार दिया। अब देखें गणक पर घटाने के बाद हमारे  पास क्या बचा। सैंकड़े के स्तंभ में मोती यानी 200; दहाई के तार में 8 मोती यानी 80; और इकाई तार में तीन मोती; कुल मिलाकर हमारे पास 283 बचा।

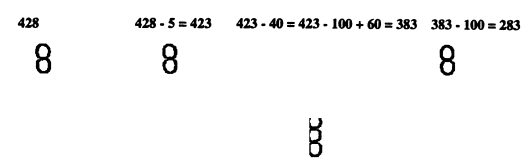
गणक पर गुणा  
वैसे देखें तो गुणा भी एक तरह का लगातार जोड़ है। गणक में इस क्रिया को करने के लिए इसी गुण का उपयोग करते हैं। जैसे कि :

   135
 x  27 

इसे इस तरह भी लिख सकते हैं 135 X 20 + 135 x 7; इस गुणा को गणक पर भी इसी तरह दो हिस्सों में करेंगे। पहले हिस्से में 135 में 7 का गुणा कर परिणाम को गणक पर प्रदर्शित करेंगे और दूसरे हिस्से में 20 का गुणा कर आने वाले संख्या को पहले के परिणाम में जोड़ देंगे। आइए इसे करके देखते हैं।

135 x 7 को इस तरह भी लिखा जा सकता है (100 + 30 + 5) x 7; इसे भी अलग-अलग करे देखें तो सबसे पहले 5 x  7  = 35; अब इस 35 को गणक पर दिखाना है। वही पुराना तरीका इकाई स्तंभ के 5 मोती और दहाई के 3 मोती ऊपर कर दिए। उसके बाद 30 x  7  = 210, इसको गणक पर दिखाई गई पहली संख्या 35 में जोड़ देंगे, सैंकड़े के तार में दो मोती और दहाई के तार में एक मोती ऊपर करके। इकाई के स्थान पर शून्य है यानी इस तार में कोई भी मोती ऊपर नहीं उठना है। अब गणक पर जो संख्या प्रदर्शित है वो है 245; अब हमें 100 का 7 में पर्याप्त मोती बचे हैं, इसलिए इस 700 को 245 में जोड़ने के लिए बस इतना करेंगे कि सैंकड़े के स्तंभ में सात मोती ऊपर उठा दिए। अब कुला जोड़ के रूप में गणक पर हमारे पास है 945:

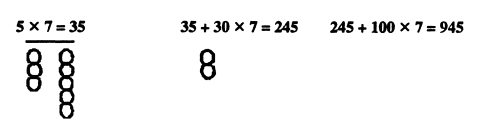
अभी दूसरा हिस्सा बचा है यानी 135 x 20; इसमें भी वही करना है कि क्रम से गुणा करते जाओ और आने वाली संख्या को गणक पर पहले प्रदर्शित संख्या में जोड़ते जाओ।

तो 5 x 20 से मिली संख्या 100; इसे गणक पहले से मौजूद 945 में जोड़ना है। सीधे-सीधे देवें तो करना यह चाहिए कि सैंकड़े के स्तंभ से एक मोती ऊपर उठा दिया जाए, लेकिन हकीकत में गणक पर सैंकड़े के तार में एक भी मोती नीचे नहीं है सारे-के-सारे नौ ऊपर है! तो फिर? जैसे कि हमने गणक पर जोड़ करते समय सीखा था, 100 जोड़ने का मतलब है कि 1000 जोड़ दो ओर 900 घटा दो। इस प्रक्रिया को करने के लिए हम हज़ार के तार से एक मोती ऊपर उठाएंगे और सैंकड़े के स्तंभ से नौ मोती नीचे गिराएंगे। अब 30 को 20 से गुणा करना है और उसे गणक पर दर्शाई गई संख्या में जोड़ना है। अंत में 100 को 20 से गुणा करना है और उसे भी गणक पर जोड़ देना है। अब देखते हैं कि गणक पर क्या स्थिति है।

हज़ार के स्तंभ में मोती ऊपर हैं यानी 3000, सैंकड़े के तार में छह मोती यानी 600; दहाई में चार मोती यानी 400; और इकाई में पांच मोती। यानी कुल जोड़ 3645 है, जो दोनों संख्याओं के गुणा के बराबर होगा।

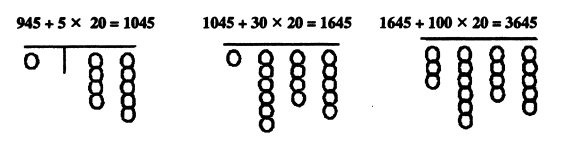
गणक पर भाग 
भाग दरअसल लगातार घटाने की विधि है और गणक पर की जाने वाली क्रियाओं में सबसे कठिन भी। इसे सीखने के लिए आइए उदाहरण के रूप में 13824 को 54 से विभाजित करते हैं। मोटे तौर पर भाग की क्रिया के लिए हम गणक को दो भागों में बांट लेते हैं, ताकि एक तरफ भाग किया जा सके और दूसरी तरफ उसके उत्तर को दर्शाया जा सके।

सबसे पहले इस संख्या 13824 को गणक पर दर्शाते हैं; गणक पर बिल्कुल बाएं से शुरू करके। यह पांच अंकों की संख्या है तो बाए कोने से पांचवें स्तंभ को इकाई मानकर क्रमश: इस संख्या को गणक पर प्रदर्शित कर दिया।

अब हमारी यह संख्या 10,000 के आसपास है ओर विभाजक लगभग 50 का है तो आने वाला हल 200 के आसपास की कोई संख्या होगी। यानी इसे इसे दर्शाने के लिए दाहिनी तरफ के तीन पर्याप्त रहेंगे। अब भग करते हैं:

54 का भाग 1 या 13 में नहीं जा सकता लेकिन 138 में दो बराबर बार जाता है; तो दाहिनी तरफ के जो तीन स्तंभ छोड़े हैं उनमें सैंकड़े के तार में दो मोती ऊपर उठा दिए; और आगे के कदम के रूप में 54 का 200 गुना यानी 10800 गणक पर दर्शाई संख्या 13824 में से घटा दिया। अब हमारे पास गणक पर बाई तरफ वाले हिस्से में बची संख्या है 3024 और दाहिनी ओर दहाई के तार में पांच मोती ऊपर उठा दिए; और 54 का 50 गुना यानी 2700 को 3024 में से घटा दिया। अंत में हमारे पास बार्इं तरफ बचे 324 और दाहिने तरफ 250; (यहां यह ध्यान रखें कि 3024 में से 2700 घटाने का मतलब है 3000 घटाना और 300 जोड़ना। अब जो संख्या हमारे पास बची है वो है 324 और 54 का इसमें सीधे-सीधे छह बार भाग जाता है, तो हमने दाहिनी तरफ इकाई के स्तंभ में छह मोती ऊपर उठा दिए। और बार्इं तरफ 54 का छह गुना यानी 324 बची संख्या 324 में से घटा दिया - बाकी बचा शून्य यानी बार्इं ओर के कोने के सारे मोती नीचे आ चुके हैं। और उत्तर 256 प्रदर्शित है गणक के दाहिनी ओर।

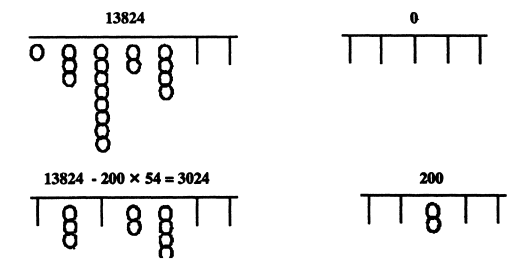
स्वाभाविक है कि गणक पर होने वाली इन सब क्रियाओं के बारे में पढ़ते हुए आपको लग रहा होगा कि जब सीधे-सीधे आंकड़ों में गुणा भाग किया जा सकता है तो फिर ये सब तामझाम क्यों? इस सवाल का कोई आसान जवाब नहीं है - यही कहा जा सकता है कि शायद पढ़ने की बजाए गणक  बनाकर ये सब गणनाएं करें तो इतना मुश्किल नहीं लगेगा। और एक बार गणक पर काम करने की आदत बन जाए तो शायद रफ्तार भी आ जाएगी प्रेक्टिस से।

(विजय शंकर वर्मा - दिल्ली विश्विद्यालय में भौतिक शास्त्र के प्राध्यापक।)

ज़रा सिर तो खुजलाइए

कोई भी बच्चा इस लड़के के साथ खेलने को तैयार नहीं है। लेकिन इसे कोई परवाह नहीं। उसने झूलन के लिए क्या तरकीब लगाई होगी