स्टीफन जे. गूल्ड
अनुवादः मनोहर नोतानी
आंकड़ों की बाज़ीगरी कमाल है सांख्यिकी का। एक दास्तां, जिसमें ऐसी ही एक गफलत का खुलासा किया गया है।
हाल ही में मेरा सामना मार्क ट्वेन की दो चुटकियों से बड़े ही निजी अंदाज़ में हुआ। इनमें से एक तो मैं इस लेख के अंत तक मुल्तवी रखता हूं। अब दूसरी चुटकी जो है वह झूठ की तीन प्रजातियों की ओर इशारा करती है - मूठ, सफेद झूठ और आंकड़े।
आंकड़ों के जरिए सच्चाई को तोड़-मरोड़कर पेश किए जाने के उस जाने पहचाने अंदाज़ को लेते हैं जो मेरी अपनी कहानी पर पूरी तरह से फिट बैठता है। सांख्यिकी में औसत की धारणा को प्रस्तुत करने के कई तरीके हैं। इनमें से एक तो है आमतौर पर इस्तेमाल किया जाने वाला समग्र औसत - कि सारी चीजों का जोड़ निकालो और उसे ( उन चीजों को ) पाने वालों की संख्या से विभाजित करो। मसलन 100 टॉफियों को 5 बच्चों में बराबर-बराबर बांटने का अर्थ यह होगा - हर बच्चे को 20-20 टॉफियां। ( इससे ज़्यादा निष्पक्ष भला हम कैसे हो सकते हैं! )
अब माध्यिका जो है वह इसी औसत की धारणा का एक अलग मापदण्ड है। माध्यिका यानी ठीक बीचों-बीच का बिन्दु। हम अगर आंकड़ों के वितरण का 'xy' अक्ष पर कोई ग्राफ लें तो उस ग्राफ का मध्य बिन्दु उस वितरण की माध्यिका होगा। यानी वह बिन्दु जिससे आधे आंकड़े छोटे होंगे और आधे आंकड़े बड़े। टॉफियों और बच्चों के उदाहरण के सिलसिले में अगर मैं उन पांच बच्चों को उनकी लम्बाई के बढ़ते क्रम में खड़ा करूं तो माध्यिका पर का बच्चा, पहले वाले दो बच्चों के मुकाबले लम्बा होगा लेकिन क्रम में आने वाले अगले दो बच्चों से तो वह निश्चित तौर पर छोटा पड़ेगा। (और अब अगर 100 टॉफियों को बच्चों की लम्बाई के हिसाब से बांटा जाना हो तो सबसे पहले वाले दो बच्चे तो गए काम से!)
एक और उदाहरण लें - अक्सर ऐसा होता है कि सत्तारूढ़ पार्टी का कोई नेता बड़े ज़ोर-शोर से कह देता है, "हमारे देश की औसत आय 15,000 रुपए सालाना प्रति व्यक्ति है।''तभी कोई विपक्षी नेता चुटकी लेकर कहता है लेकिन हमारे आधे नागरिक तो 10,000 रुपए सालाना से भी कम कमाते हैं। दोनों ही सही हैं। पहला वाला नेता औसत का सहारा लेता है तो दूसरा नेता माध्यिका का। ( ऐसे मामलों में औसत हमेशा माध्यिका से बड़ा होता है, क्योंकि जहां तक औसत का सवाल है एक ही करोड़पति कई सौ गरीबों पर भारी पड़ सकता है। लेकिन माध्यिका की गणना में वह करोड़पति सिर्फ एक ही फकीर को हटा सकता है।)
लेकिन आंकड़ों (सांख्यिकी) के प्रति शक और कड़वाहट पैदा करने वाला जो व्यापक मुद्दा है वह ज़्यादा तकलीफदेय है। बहुत से लोग दिल और दिमाग, जज़्बात और अक्लमंदी के बीच फर्क करते हैं। यह फर्क गलत तो है ही, दुर्भाग्यपूर्ण भी है। कुछ मौजूदा विश्वास भावनाओं को ही असल चीज़ मानते हैं। ऐसे समाजों में कोई भी काम करने का उचित आधार भावनाएं ही मानी जाती हैं। बुद्धि को हमेशा निचली सीढ़ी पर ठेल दिया जाता है। इस सबके चक्कर में पिसती है तो बेचारी सांख्यिकी।
मेरी अपनी कहानी आंकड़ों की निजी दास्तान है। और अगर इसे सही तरीके से लिया जाए तो यह काफी प्रेरणास्पद भी है। मेरी इस कहानी में विज्ञान के रूखे-सूखे, शास्त्रीय ज्ञान की उपयोगिता की ओर इशारा किया गया है। दरअसल दिल और दिमाग तो एक ही व्यक्ति के एक ही शरीर के दो हिस्से हैं।
हुआ यह कि जुलाई 1982 में मुझे पता चला कि मुझे पेट का कैंसर (एब्डॉमिनल मेसोथेलिओमा) हो गया है। यह कैंसर, जो कि एस्बेस्टॉस की वजह से होता है, काफी गंभीर और बिरले ही होता है। ऑपरेशन के बाद मैं थोड़ा ठीक हुआ तो डॉक्टर से मेरा सबसे पहला सवाल था "मेसोथेलिओमा पर सबसे बढ़िया तकनीकी साहित्य क्या है?" लेकिन उसने बड़ी चतुराई से मेरे इस सवाल को यह कह कर टाल दिया कि इस बीमारी पर उपलब्ध मेडिकल साहित्य में कहीं भी ऐसा कुछ नहीं है जो उपयोगी हो।
सिर्फ यही एक ऐसा वाकया है, जहां मेरी उस डॉक्टर ने मुझसे बेझिझक सच न कह कर टालमटोल का रास्ता अपनाया था। खैर एक बुद्धिजीवी को साहित्य से अलग-थलग रखना उतना ही मुश्किल होता है जितना इंसान की मौजूदा प्रजाति से ब्रह्मचर्य का पालन करवाना। बीमारी के बाद जैसे ही मैं चलने-फिरने के काबिल हुआ, मैंने सीधे हार्वर्ड विश्व विश्विद्यालय की ओर रुख किया। वहां के मेडिकल पुस्तकालय में मैंने पेट के कैंसर से
औसत बनाम माध्यिका
अगर यह मान लें कि हम किसी एक ऐसे देश के निवासी हैं, जिसमें कुल नागरिकों की संख्या मात्र 11 है। और इन नागरिकों की वार्षिक आय बढ़ते हुए क्रम में कुछ इस प्रकार है
सभी नागरिकों की कुल आय = 1,65,000
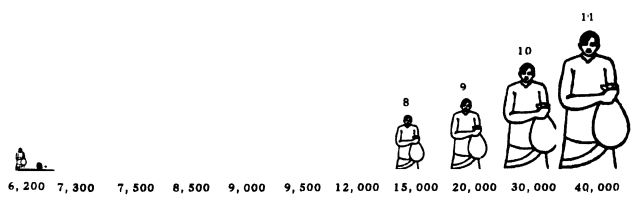
सत्तारूढ़ पार्टी का नेता जिस औसत की बात कर रहा है उसे सांख्यिकी में अंकगणितीय औसत कहा जाता है।
अंकगणितीय औसत = सभी मूल्यों का कुल योग / वस्तुओं की कुल संख्या
यह तो हुआ औसत की धारणा का एक पैमाना। दूसरे मापदण्ड यानी माध्यिका, का माप पता करने के लिए हमें पहले उस समूह की सभी वस्तुओं को क्रमवार व्यवस्थित करना पड़ता है।
मसलन, काल्पनिक देश के नागरिकों की माध्यिका वार्षिक आय जानने के लिए हमने ऊपर दी गई तालिका और रेखाचित्र दोनों में ही नागरिकों को वार्षिक आय के बढ़ते हुए क्रम में दर्शाया है। अब ऐसे एक क्रम में जो सबसे बीच की वस्तु होगी उसके मान को ही सांख्यिकी में माध्यिका कहते हैं। क्रम में माध्यिका मान वाली वस्तु के आगे जितनी वस्तुएं होंगी उतनी ही पीछे होंगी। यानी 3 वस्तुओं के क्रम में दूसरी वस्तु का मान माध्यिका होगा, 7 वस्तुओं के क्रम में चौथी वस्तु का और 11 वस्तुओं के क्रम में छठी वस्तु का मान आदि।
इस जानकारी के आधार पर यह स्पष्ट हो जाता है कि दोनों नेता अपनी अपनी जगह सही हैं। तालिका और ग्राफ में दिए आंकड़ों के अनुसारः
देश की औसत वार्षिक आय = सभी आयों का अंकगणितीय औसत
= सभी नागरिकों की कुल वार्षिक आय / देश में नागरिकों की कुल संख्या
= रु. 1, 65, 000/11
= 15, 000 रुपए सालाना प्रति व्यक्ति
देश की माध्यिका आय = नागरिकों की क्रमवार तालिका में बीच के नागरिक की सालाना आय
= छठे नागरिक की आय
= 9, 500 रुपए प्रति साल
ग्राफ और तालिका से साफ ज़ाहिर है कि माध्यिका आय वाला नागरिक ( नागरिक क्रमांक 6 ) देश की जनसंख्या को बराबर दो समूहों में बांटता है। - आधा हिस्सा उन लोगों का जिनकी सालाना आमदनी 10, 000 रुपए से भी कम है, और बाकी के आधे हिस्से में वे नागरिक आते हैं जिनकी वार्षिक आय 10, 000 रुपए से अधिक है अर्थात, इस काल्पनिक देश की औसत आय 15, 000 रुपए प्रति व्यक्ति होते हुए भी देश की आधी जनता 10,000 रुपए सालाना प्रति व्यक्ति से भी कम कमाती है।
सम्बन्धित सारी हालिया सामग्री खोज निकाली। एक घंटे बाद जब मैं सारा साहित्य पढ़ चुका तो मेरा माथा ठनका।
मुझे समझ में आया कि मेरी उस डॉक्टर ने मुझे उस तल्ख सच्चाई से दूर क्यों रखा था। सारे-के-सारे पन्ने मानो अपनी पूरी वहशियत में मुझसे चीख चीख कर कह रहे थे - मेसोथेलिओमा का कोई इलाज नहीं है; पता चलने के बाद मरीज़ की औसत ( माध्यिका ) उम्र तकरीबन 8 महीने है। कुछ देर तक तो मैं धरा-का-धरा रह गया। मेरी तो कुछ समझ में नहीं आ रहा था। खैर थोड़ी देर बाद मैं मुस्कुराया और मैंने अपने आप से कहा, "तो यह बात थी जिसके कारण उन्होंने मुझे इस बारे में पढ़ने को कुछ नहीं दिया।'' शुक्र है मेरा दिमाग फिर चलने लगा।
यदि अल्पज्ञान कहीं खतरनाक होता है तो इससे बढ़िया उदाहरण भला मेरे लिए और क्या हो सकता था? अपनी बीमारी को समझते-समझते मैं यह जानने लगा था कि कैंसर से लड़ने में मनः स्थिति बहुत मायने रखती है। पता नहीं क्यों। ( हालांकि मेरे पुराने पदार्थवादी दृष्टिकोण के हिसाब से मेरा अनुमान है कि मनःस्थिति हमारी प्रतिरक्षण प्रणाली को कमजोर या पुख्ता बनाने में महत्वपूर्ण रोल निभाती है।) दरअसल यदि सारी चीजें जैसे, उम्र, तबका, तंदरुस्ती व सामाजिक-आर्थिक स्थिति वगैरह लगभग समान हों तो यह पाया गया है कि एक ही प्रकार के कैंसर से पीड़ित वे लोग तुलनात्मक रूप से ज्यादा जीते है जोः
- जीवन के प्रति सकारात्मक रवैया अपनाते हैं।
- जिनकी इच्छाशक्ति प्रबल होती है।
- जिनके पास जीने का कोई पुख्ता मकसद होता है।
- जो किसी भी तरह के संघर्ष के लिए तैयार रहते हैं।
- जो अपने इलाज व अपनी चिकित्सा की प्रक्रिया में अपने डॉक्टर द्वारा कही गई बात को शब्दशः निक्रिय । रूप से स्वीकार नहीं करते, बल्कि ठीक होने में अपनी सक्रिय भूमिका निभाते हैं।
कुछ महीनों बाद अपने वैज्ञानिक गुरु व प्रतिरक्षण के क्षेत्र में नोबल पुरस्कार प्राप्त सर पीटर मेदावर से मैंने पूछा कि कैंसर से लड़ने का सबसे बढ़िया नुस्खा भला क्या है?
उनका कहना था, "एक खुशगवार व्यक्तित्व" सौभाग्य से अगर मैं कुछ हूं तो यही हूं। हौसले से भरपूर और ठंडे मिज़ाज का, कम-से-कम इस मामले में तो। (वैसे भी किसी खास मकसद के लिए एकदम से अपने-आप को एक नए ही रूप में डाल पाना कमोबेश नामुमकिन ही होता है।)
इसलिए संवेदनशील डॉक्टर अक्सर इस दुविधा में पड़ते हैं। ऐसे में निराशाजनक निष्कर्ष को उजागर करना क्या ठीक होगा, खासकर तब जबकि मनःस्थिति बहुत मायने रखती हो? फिर बहुत कम लोग सांख्यिकी का इतना ज्ञान रखते हैं कि वे ऐसे किसी कथन की जांच पड़ताल सही-सही कर सकें और उसका उचित मूल्यांकन कर सकें। मेरे अपने मामले में मुझे पूरा यकीन है कि मेरा जीवन बचाने में उस तकनीकी समझ का भी बहुत बड़ा रोल था जो मैंने अपने विषय यानी प्रकृति विज्ञान ( नेचुरल हिस्ट्री ) में काम करते हुए पाई है।
इस सारी समस्या को संक्षिप्त रूप से यूं बांचा जा सकता है, “फलां बीमारी की औसत घातकता या यूं कहें कि जानलेवापन, आठ महीने है?" आप ही बताइए हमारी अपनी बोलचाल की भाषा में इसका अर्थ क्या निकलता है? मुझे तो लगता है ज्यादातर लोग जिन्हें सांख्यिकी का ज्ञान नहीं है इस कथन को यूं लेंगे, "मैं संभवतः आठ महीने के भीतर चल बसूंगा।"
इसी निष्कर्ष से तो बचना है। सिर्फ इसलिए नहीं कि ( इस कथन द्वारा ) इस नतीजे पर पहुंचना सिद्धांततः गलत है, बल्कि इसलिए भी क्योंकि मनःस्थिति ऐसे मामलों में बहुत मायने रखती है। यह सही है कि मैं बहुत खुश नहीं हुआ था। लेकिन मैंने ऐसा निराशावादी रवैया भी नहीं अपनाया। मेरी तकनीकी मशक्कत के कारण मैं ‘आठ महीने की औसत घातकता' कथन को एक अलग अंदाज़ से देख पाया। हालांकि मेरी बात काफी बारीक किस्म की लग रही होगी, लेकिन इसके असर काफी गंभीर और व्यापक हो सकते हैं। फिर इस तरह की सोच मेरे अपने विषय, प्रकृति विज्ञान और जीव विकास, की विचारधारा को साकार भी करती है। हम आज भी प्लेटो की उस परंपरा का बोझ ढो रहे हैं जिसके तहत आम चीजों को एकदम निश्चित जड़ खांचों सोच के कारण हम औसत के सांगिकी में फिट करने के आदी हो गए हैं (और पैटर्न को गलत अंग से देखने लगते हैं। इसीलिए हम 'जीवन की एकदम साफ- बल्कि यूं कहें ठेठ इसी कारण हम असल साफ शुरु आत' या 'मृत्यु की परिभाषा' दुनिया को, उसकी विविधताओं को, जैसी कोशिशों में उलगे रहते हैं। जबकि उसकी विभिन्न रंगतों को, ठीक उल्टा ही प्रकृति अक्सर हमें गच्चा दे जाती है लेते हैं। संक्षेप में कहूं तो हम सांख्यिकी और हमारे सामने एक कभी न टूटने औसत व माध्यिका गणनाओं को ही वाली निर्वाध निरंतरता के रूप में पेश सरासर सच मान बैठते हैं और इन आती रहती है।)
चीजों को एकदम साफ-साफ- विभाजन करने और उन्हें अपरिवर्तनशील हिस्सों में बांटने की हमारी एक प्लेटोनिक सोच के कारण हम औसत के सांख्यिकी पैटर्न को गलत ढंग से देखते हैं बल्कि यूं कहें ठेठ इसी कारण हम असल दुनिया कोण, उसकी विविधताओं को, उसकी विभिन्न रंगतों को, ठीक उल्टा ही लेते हैं संक्षेप मे कहूं तो हम सांख्यिकी औसत व माध्यिका गणनाओं को ही सरासर सच मान बैठते हैं गणनाओं को संभव बनाने वाली घटबड़ (अलग-अलग आंकड़ों ) को हम इस छुपी हुई गुड़ सच्चाई का अस्थाई व त्रुटिपूर्ण पैमाना भर मान लेने की गलती करते है।
चीजों को एकदम साफ-साफ पी विभाजन करने और उन्हें अपरिवर्तनशील हिस्सों में बांटने की हमारी इस प्लेटोनिक
अब यदि माध्यिका ही सच्चाई है और उसके आसपास मंडराने वाले आंकड़े उस सच्चाई तक पहुंचने के औज़ार मात्र हैं तो मैं तो गया काम से। फिर तो मुझे मानना ही पड़ेगा, "आठ महीनों के भीतर ही मुमकिन है मैं दुनिया से खिसक लूंगा।"
लेकिन सारे विकासवादी जीवशास्त्री मानते हैं कि यह घटबढ़, यह वैविध्य ही प्रकृति का सार है। घटबढ़ सिर्फ औसत निकालने का कोई दोषपूर्ण ज़रिया भर नहीं है। देखा जाए तो स्वयं औसत व माध्यिका ही अमूर्त है। इसलिए मैं कैंसर संबंधी आंकड़ों को अलग नज़रिए से देख पाया। और सिर्फ इस कारण नहीं कि मैं आशावादी हूं बल्कि इसलिए भी कि मैं जानता हूं कि विविधता ही वास्तविकता है। मुझे अब इन तमाम आंकड़ों के बीच अपनी जगह तलाशना थी।
जब मैंने आठ महीने की माध्यिका के बारे में जाना तो मेरी पहली सोची समझी प्रतिक्रिया यही थी कि तो अच्छा, आधे लोग इससे ज्यादा जिएंगे। इन आधों में मेरी भी गिनती हो, इसकी कितनी संभावना है? अगला एक घंटा मैंने, अपने सारे डर, अपनी तमाम बेचैनियों के बीच, पढ़ते हुए बिताया और एक सुकून भरे नतीजे पर पहुंचा। मैं उन सारी खूबियों का मालिक था जिनके कारण लंबे जीवन की आस बंधती थी। मैं जवान था, मेरी बीमारी कमोबेश शुरुआती दौर में ही पता चल गई थी, मुझे अपने देश का सबसे बढ़िया इलाज मुहैया हो सकता था। मेरे जीने के लिए सारी दुनिया थी। और फिर मैं जानता था कि आंकड़े कैसे
सही-सही पढ़े जाएं ताकि हम निराश न हों।
एक अन्य तकनीकी मुद्दे से भी मुझे आशा बंधी। जल्दी ही मेरी समझ में आया कि इस आठ माह की माध्यिका के आसपास के आंकड़ों का जो वितरण होगा वह कमोबेश सांख्यविदों की भाषा में "दाहिनी ओर का ढलवा' होगा।
(दरअसल मोटे तौर पर आंकड़ों के दो तरह के वितरण देखे जा सकते हैं - संतुलित वितरण और असंतुलित वितरण। संतुलित वितरणों में माध्यिका बिंदु के बाईं ओर का हिस्सा, दाहिने ओर के हिस्से का प्रतिबिंब होता है। असंतुलित वितरण दो तरह के हो सकते हैं - दाहिनी और के ढलवां वितरण और बाईं ओर के ढलवां वितरण। दाहिनी ओर के ढलवां वितरण में माध्यिका के दाहिनी ओर का हिस्सा, माध्यिका के बाईं ओर के हिस्से के मुकाबले ज्यादा दूर तक जाता है। जबकि बाईं ओर के ढलवां वितरण में स्थिति इससे ठीक उलट होती है। यानी माध्यिका के बाईं ओर का हिस्सा दाहिने के मुकाबले ज्यादा लंबा खिंचता है।)
मेरे मामले में तो यह वितरण दाहिनी ओर का ढलवां होना ही था; ऐसा मेरा तर्क था। बाईं ओर का हिस्सा अपने साथ उस अटल, कभी न हिलने वाली निचली सीमा-रेखा को जो समेटे था, जिसे हम शून्य कहते हैं ( आखिर कैंसर का पता मृत्यु के समय या उसके पहले ही लग सकता है)। इसलिए इस वितरण में निचले ( या बाएं) आधे हिस्से के लिए जगह की कमी होनी ही थी। यानी शून्य व
क. संतुलित वितरण - इसमें माध्यिका के दाहिनी और का हिस्सा बाईं ओर के हिस्से का प्रतिबिंब होता है। ,
ख. दाहिना ढलवां वितरण - यह दिखाते हुए कि ऐसे वितरण में औसत, माध्यिका से बड़ों होता है और पूंछ दाहिनी और दूर तक जाती है।
ग. दायां ढलवां वितरण - ऐसे वितरण में औसत, माध्यिका से छोटा होता है।
आठ-माह की सीमा-रेखाओं के बीच उस वितरण का कूबड़ उठा होना था। जहां तक ऊपरी (या दाहिने ) आधे हिस्से की बात थी तो उसकी पूंछ तो काफी दूर तक जा सकती थी; यानी आठ महीने के बाद से कितने भी सालों तक जा सकती थी। फिर चाहे, अंततः कोई न बचता हो। अब चूंकि मैं यह तो जान ही चुका था कि मेरी अपनी अनुकूल शख्सियत के कारण मैं उस वांछनीय दाहिने हिस्से में ठीया ( जगह ) पाने का अच्छा-खासा दावेदार था, इसलिए अब इतना ही जानना मेरे लिए बाकी था कि आखिर पूंछ दाहिनी ओर कितनी दूर तक जाती है?
और वास्तव में यह वितरण दाहिना ढलवां था - एक लंबी पूंछ (चाहे कितनी भी पतली ) के साथ। यह पूंछ आठ माह की माध्यिका से कई साल आगे तक जाती थी। मुझे उस छोटी-सी पूंछ में अपने न हो सकने का कोई कारण नहीं नज़र आया। मैंने राहत की सांस ली। मेरे तकनीकी ज्ञान ने मेरी मदद की थी। मैंने आंकड़ों के वितरण को सही-सही पढ़ा था। मैने सही सवाल पूछे थे और जवाब भी पाए। मैने शायद वह पाया था, जिसे उन परिस्थितियों में सबसे कीमती तोहफा कह सकते हैं- खूब सारा समय। जल्दबाजी की कोई ज़रूरत नहीं थी मुझे। मौत का
*मान लीजिए 100 लोगों को वह कैंसर था। पता लगने के बाद हुए व्यक्ति कितने महीने जीवित रहा - इस बात के आंकड़ों को कम से ज़्यादा के क्रम में जमा दिया जाए। पता लगने के बाद से कुछ की मृत्यु एक महीने में हो गई, कुछ की 3 महीने में आदि। पचासवें मरीज़ की मृत्यु 8 महीने बाद ई। बाकी के 50 मरीजों की मृत्यु 9 महीने से लेकर कितने भी सालों तक होती रही। यदि बीमारी जानने के बाद एक भी मरीज़, मान लीजिए बस साल तक जी जाए तो ग्राफ में 8 महीने के बिन्दु ( जो माध्यिका है) और 10 साल के बिन्दु के बीच का अंतराल शून्य से 8 माह के बिन्दु के अंतराल से कहीं ज़्यादा लंबा होगा। इसीलिए इस ग्राफ में माध्यिका के दाहिनी ओर से ज़्यादा ली होगी और बाईं ओर का हिस्सा छोटा होगा।
साया मेरे सिर पर नहीं मंडरा रहा था। चिन्ता की कोई बात नहीं थी। मेरे पास समय था - सोचने के लिए तैयारी करने के लिए, लड़ने के लिए।
सांख्यिकी वितरणों संबंधी एक बात और-वे किन्हीं 'नियत' परिस्थितियों पर ही लागू होते हैं। (जैसे कि मेरे किस्से में मसला था - चिकित्सा की परंपरागत पद्धतियों द्वारा पेट के कैंसर के इलाज के बाद मेरे बचने की संभावनाएं)
परिस्थतियां अगर बदल जाएं तो इन वितरणों की रूपरेखा भी बदल सकती है। मैं तो अपने इलाज के दौरान जिन विधियों से गुज़रा उन्हें आज़माइशी ही कहा जा सकता है। और अगर किस्मत रही तो मैं उस नए वितरण के सबसे पहले दस्ते का बाशिंदा होऊंगा, जिसकी माध्यिका ऊंची होगी; और जिसकी दाहिनी पूंछ वृद्धावस्था में कुदरती वजहों से होने वाली मौत तक जाती होगी।
मैं देखता हूं कि मौत को स्वीकार करने की बराबरी आंतरिक गरिमा से करने का चलन इधर कुछ ज्यादा ही हो चला है। मैं मानता हूं कि हर चीज़ का अपना-अपना वक्त होता है - प्यार का वक्त, मरने का वक्त। और मेरी डोर जब खत्म होगी तो मुझे उम्मीद है कि मैं भी अपनी मौत का सामना अपने ढंग से शांति के साथ कर सकूंगा। लेकिन अधिकांश परिस्थितियों में तो मैं मौत को अंतिम शत्रु मानने वाले पदार्थवादी दृष्टिकोण का हिमायती ही रहूंगा। जो रोशनी बुझने के खिलाफ अपनी जंग जारी रखते हैं, उनके लिए मेरे मन में कोई दुराव नहीं है।
लड़ाई की तलवारें तो अनेक हैं लेकिन हंसी-ठट्टे से ज़्यादा प्रभावी कोई नहीं। मेरे मित्रों की एक मीटिंग में मेरी मौत की घोषणा की गई और मैं अपनी ही श्रद्धांजली का मज़ा लेने से चूक गया। हुआ यह कि श्रद्धांजली मेरे एक करीबी दोस्त द्वारा लिखी जानी थी। ( लेकिन मेरा वह दोस्त स्वयं एक सांख्यिकी-शास्त्री होने के नाते आंकड़ों के वितरण में मुझे बाईं ओर पाने के बारे में सोच नहीं सकता था। वह शंकित हुआ और उसने मेरी मौत की इस खबर की पुष्टि करना ही उचित समझा।) ज़रा सोचिए मेरे मुंह पर मार्क ट्वेन की सबसे मशहूर पंक्ति तकरीबन आ ही चुकी थीः ‘मेरी मौत की खबरें अतिशयोक्तिपूर्ण है।'
(मनोहर नोतानी - एकलव्य के प्रकाशन स्रोत से संबद्ध )
स्टीफन जे. गूल्ड - हार्वर्ड विश्वविद्यालय (अमेरिका) में भू-विज्ञान एवं प्राणीशास्त्र के प्रोफेसर जैव विकास और जीवाश्म के अध्ययन में महारत। विभिन्न विषयों पर लगातार लेखन।