पुस्तक अंश
भाग - 5
शेषािगरी केएम राव
“शायद सबसे बड़ा विरोधाभास तो यही है कि गणित में विरोधाभास होते हैं।”
- एडवर्ड कैसनर
क्या आपने कभी कोनिग्सबर्ग के सात पुलों के बारे में, चार रंगों की समस्या के बारे में, हज्जाम विरोधाभास के बारे में या फर्मा के अन्तिम प्रमेय के बारे में सुना है? यदि नहीं सुना है, तो मैं आपको बताना चाहूँगा कि ये गणित के सबसे दिलचस्प और पेचीदा सवालों में से हैं जिन्होंने कई पीढ़ियों के सर्वोत्तम दिमागों को, और कभी-कभी तो सैकड़ों वर्षों तक छकाया है! इन सवालों को हल करते-करते गणितज्ञों ने विषय की सर्वथा नवीन शाखाओं का आविष्कार किया है। इन आविष्कारों ने फिर गणितीय खोजबीन को आगे बढ़ाया है।
चन्ना ने हमें अतीत की इन पड़तालों की दिलकश कहानियाँ सुनाईं। मुझे वे कहानियाँ आज तक याद हैं। मैंने यथासम्भव बढ़िया ढंग से ये कहानियाँ अपने छात्रों को सुनाईं। मैं अक्सर हैरान रह जाता हूँ कि इन्हें हमारे पाठ्यक्रम में शामिल क्यों नहीं किया गया है। लगता तो ऐसा है कि पाठ्यक्रम की रचना ही हमारे स्कूली जीवन को नीरस बनाने के लिए की गई है।
हमारे शिक्षक के नाते, चन्ना चाहते थे कि हमें उस प्रक्रिया की झलक मिले जिसके माध्यम से वास्तव में गणित का सृजन होता है। इसलिए उन्होंने ऐसे कुछ प्रमुख सवाल हमारे साथ साझा किए थे, जिन्होंने इस विषय के विकास में योगदान दिया है। मुझे इनमें से चार याद हैं और मैं उन्हें आपके सामने पेश करना चाहूँगा। यकीन मानिए, एक क्षण भी उबाऊ नहीं होगा।
सबसे पहले कोनिग्सबर्ग के सात पुल - यह कहानी तो बतानी ही होगी।
कोनिग्सबर्ग के सात पुल
मुझे पक्का याद नहीं कि यह किस कक्षा की बात है। शायद नौंवी या दसवीं की बात होगी जब हम मैट्रिक्स (आव्यूह) का विचार सीखने ही वाले थे। चन्ना ने बात की शुरुआत आव्यूह की परिभाषा (“आव्यूह संख्याओं की एक क्षितिज व उर्ध्वाधर व्यवस्थित सारणी होती है”) देकर और यह बताकर नहीं की थी कि “इनको जोड़ने व गुणा करने के नियम होते हैं।” जब यह नहीं किया तो पाठ्यपुस्तक के सम्बन्धित उबाऊ सवाल की तो बात ही नहीं आई। चन्ना ने तो कुछ एकदम अलग ही किया था। उन्हें तो इस विचार की जड़ तक जाना था और इस खोजबीन के रोमांच में अपने छात्रों को शामिल करना था। और इस तरह से हमें 300 साल पुरानी ‘कोनिग्सबर्ग के सात पुल’ पहेली की दावत मिली।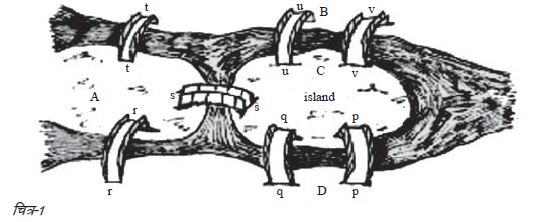 मुझे याद है हमने दो पीरियड तो इस पहेली की चर्चा करते बिताए होंगे, जो रोज़मर्रा के जीवन से उभरी थी। इसने ग्राफ सिद्धान्त जैसे गणित के नए क्षेत्रों के विकास का मार्ग प्रशस्त किया था। विज्ञान व इंजीनियरिंग में ग्राफ सिद्धान्त का काफी उपयोग होता है। इससे जुड़ा आव्यूहों (matrices) का विचार है जिनका उपयोग जटिल दृश्य प्रस्तुतीकरण को सरलीकृत करने में किया जाता है। आव्यूह क्वांटम मेकेनिक्स में भी महत्वपूर्ण हैं। क्वांटम मेकेनिक्स भौतिकी की वह शाखा है जिसका सम्बन्ध उप-परमाणविक विश्व के रहस्यमयी कामकाज से है। दरअसल, ‘मैट्रिक्स मेकेनिक्स’ नामक कोई चीज़ भी होती है।
मुझे याद है हमने दो पीरियड तो इस पहेली की चर्चा करते बिताए होंगे, जो रोज़मर्रा के जीवन से उभरी थी। इसने ग्राफ सिद्धान्त जैसे गणित के नए क्षेत्रों के विकास का मार्ग प्रशस्त किया था। विज्ञान व इंजीनियरिंग में ग्राफ सिद्धान्त का काफी उपयोग होता है। इससे जुड़ा आव्यूहों (matrices) का विचार है जिनका उपयोग जटिल दृश्य प्रस्तुतीकरण को सरलीकृत करने में किया जाता है। आव्यूह क्वांटम मेकेनिक्स में भी महत्वपूर्ण हैं। क्वांटम मेकेनिक्स भौतिकी की वह शाखा है जिसका सम्बन्ध उप-परमाणविक विश्व के रहस्यमयी कामकाज से है। दरअसल, ‘मैट्रिक्स मेकेनिक्स’ नामक कोई चीज़ भी होती है।
वैसे मैं नहीं जानता कि आव्यूह का विषय हमारे स्कूल पाठ्यक्रम में कैसे स्थान पा गया था, लेकिन मुझे खुशी है कि इसे स्थान मिला। आखिर इसी की बदौलत तो हमें यह अद्भुत कहानी सुनने को मिली।
सात पुल की पहेली 1254 में प्रशिया स्थित कस्बे कोनिग्सबर्ग में उपजी थी। आजकल यह रूस में कालिनिनग्राद है। कोनिग्सबर्ग कस्बा चार छोटे-छोटे टापुओं से बना था। ये टापू एक-दूसरे से और मुख्य भूमि से सात पुलों के माध्यम से जुड़े थे। ये पुल प्रेजेल नदी पर बने थे जो कोनिग्सबर्ग में से होकर गुज़रती थी। इन सात पुलों (आज इनमें से कोई भी अस्तित्व में नहीं है) को नाम दिए गए थे: ब्लैकस्मिथ, कनेक्टिंग, ग्रीन, मर्चेंट, वुडन, हाई और हनी।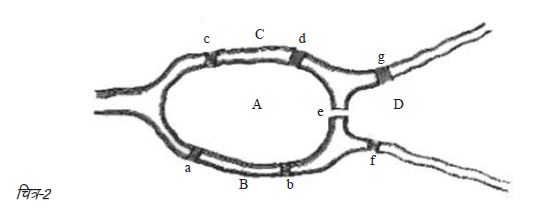 लोककथा के मुताबिक चुनौती यह थी कि कोनिग्सबर्ग शहर का चक्कर इस तरह लगाया जाए कि आप प्रत्येक पुल पर से एक ही बार गुज़रें और शुरुआती बिन्दु पर लौट आएँ। क्यों न आप चित्र-1 में दिए गए पुलों के चित्र पर ऐसा रास्ता बनाकर देख लें? 1736 में सेंट पीटर्सबर्ग एकेडमी के निमंत्रण पर, लिओनहार्ड ओइलर ने दिखा दिया था कि अपने कदमों पर लौटे बगैर सातों पुलों को पार करना असम्भव है। उन्होंने इस तरह के सवाल सुलझाने के लिए एक कसौटी भी प्रस्तुत की थी। चूँकि वह कसौटी कोनिग्सबर्ग पहेली पर लागू नहीं होती, इसलिए उस पहेली का कोई हल नहीं है। इससे पहले कि हम थोड़ी और चर्चा करें, चन्द मिनट लेकर ओइलर द्वारा बनाए गए इस पहेली के रेखाचित्र (चित्र-2) पर गौर कीजिए।
लोककथा के मुताबिक चुनौती यह थी कि कोनिग्सबर्ग शहर का चक्कर इस तरह लगाया जाए कि आप प्रत्येक पुल पर से एक ही बार गुज़रें और शुरुआती बिन्दु पर लौट आएँ। क्यों न आप चित्र-1 में दिए गए पुलों के चित्र पर ऐसा रास्ता बनाकर देख लें? 1736 में सेंट पीटर्सबर्ग एकेडमी के निमंत्रण पर, लिओनहार्ड ओइलर ने दिखा दिया था कि अपने कदमों पर लौटे बगैर सातों पुलों को पार करना असम्भव है। उन्होंने इस तरह के सवाल सुलझाने के लिए एक कसौटी भी प्रस्तुत की थी। चूँकि वह कसौटी कोनिग्सबर्ग पहेली पर लागू नहीं होती, इसलिए उस पहेली का कोई हल नहीं है। इससे पहले कि हम थोड़ी और चर्चा करें, चन्द मिनट लेकर ओइलर द्वारा बनाए गए इस पहेली के रेखाचित्र (चित्र-2) पर गौर कीजिए।
ओइलर ने किया यह था: पुलों के संजाल को उन्होंने सरल ग्राफ का रूप दे दिया था, जैसा कि चित्र-3 में दर्शाया गया है। इसमें चार शीर्ष या मार्गसंगम हैं (A, B, C और D) तथा सात किनारे या मार्ग (t, s, r, p, q, u और v) हैं।
यदि आप ध्यान से देखेंगे तो यह ग्राफ पुलों के पहले चित्रण (चित्र-1) से मेल खाता है। दरअसल, यह यथार्थ विश्व की इस पहेली की ग्राफीय प्रस्तुती है।
अब सवाल यह है: क्या कोई ऐसा रास्ता सम्भव है, जिस पर चलकर प्रत्येक रेखा पर से मात्र एक बार गुज़रेंगे और लौटकर शुरुआती बिन्दु पर आ जाएँगे - यानी क्या आप एक बन्द परिभ्रमण कर सकते हैं? करके देखिए।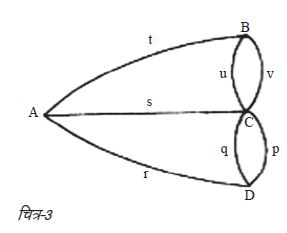 इस तरह का ग्राफ किसी परिघटना (यहाँ एक यथार्थ परिघटना यानी कोनिग्सबर्ग पुल) का दृश्य निरूपण है। इसे एक आव्यूह के रूप में भी दर्शाया जा सकता है, जो संख्याओं की एक जमावट होती है। जब ग्राफ जटिल से जटिल होने लगते हैं, तब आव्यूह परिघटनाओं के प्रस्तुतीकरण, उनमें हेरफेर करने और उनका अध्ययन करने के कारगर औज़ार साबित होते हैं, खास तौर से जब आप इस काम को कम्प्यूटर की मदद से करें।
इस तरह का ग्राफ किसी परिघटना (यहाँ एक यथार्थ परिघटना यानी कोनिग्सबर्ग पुल) का दृश्य निरूपण है। इसे एक आव्यूह के रूप में भी दर्शाया जा सकता है, जो संख्याओं की एक जमावट होती है। जब ग्राफ जटिल से जटिल होने लगते हैं, तब आव्यूह परिघटनाओं के प्रस्तुतीकरण, उनमें हेरफेर करने और उनका अध्ययन करने के कारगर औज़ार साबित होते हैं, खास तौर से जब आप इस काम को कम्प्यूटर की मदद से करें।
कोनिग्सबर्ग पहेली को एक आसन्नता आव्यूह (एडजेसेंसी मैट्रिक्स) के रूप में प्रस्तुत किया जा सकता है। यह चित्र-4 जैसा दिखता है। इसमें यह सूचना होती है कि हर शिरोबिन्दु (vertex) अन्य शिरोबिन्दुओं से किस तरह जुड़ा है।
आप शायद सोच रहे होंगे कि आव्यूह में हमें 0, 1 और 2 कैसे मिले। रेखाचित्र में किसी बिन्दु A से उसी बिन्दु तक पहुँचने वाले मार्गों की संख्या 0 है। बिन्दु A से बिन्दु B को जोड़ने वाले मार्गों की संख्या 1 है और बिन्दु B को बिन्दु C से जोड़ने वाले मार्गों की संख्या 2 है। यही बात शेष मार्गों पर भी लागू होती है (चित्र-3)।
कभी-कभी रेखाचित्र में दिख रहे शिरोबिन्दुओं के गुणधर्मों के लिए हम ‘डिग्री’ शब्द का उपयोग भी करते हैं। डिग्री सम भी हो सकती है और विषम भी। यदि कोई विषम शिरोबिन्दु है तो इसका मतलब यह होता है कि उस शिरोबिन्दु से निकलने वाले रास्तों की संख्या विषम संख्या है। कोनिग्सबर्ग चित्र में A विषम है और उसी तरह से B, C और D भी विषम हैं। हम कह सकते हैं कि उनकी डिग्री क्रमश: 3, 3, 5 और 3 हैं। यदि किसी चित्र में दो से अधिक विषम शिरोबिन्दु हों तो बगैर किसी मार्ग पर दोबारा चले उसे पार नहीं किया जा सकता। ओइलर ने यही दर्शाया था। यही वजह है कि कोनिग्सबर्ग समस्या का कोई समाधान नहीं है।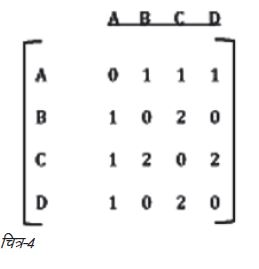 चित्र-4 के आव्यूह में रेखाचित्र की जानकारी अपेक्षाकृत सरल रूप में समाहित है। A, B, C और D स्तम्भों को अलग-अलग जोड़ लें। क्या मिला? क्रमश: 3, 3. 5 और 3, ठीक है? इस तरह रेखाचित्र के स्थान पर आव्यूह निर्मित किया जा सकता है। इसी तरीके से लोगों ने जटिल व उलझे हुए रेखाचित्रों की जानकारी को दर्शाने के लिए आव्यूह का इस्तेमाल शुरू किया था (वैसे कोनिग्सबर्ग रेखाचित्र उतना जटिल नहीं है)। कई मायनों में आव्यूह का उपयोग वास्तविक दुनिया की परिघटनाओं के प्रस्तुतीकरण में किया जा सकता है।
चित्र-4 के आव्यूह में रेखाचित्र की जानकारी अपेक्षाकृत सरल रूप में समाहित है। A, B, C और D स्तम्भों को अलग-अलग जोड़ लें। क्या मिला? क्रमश: 3, 3. 5 और 3, ठीक है? इस तरह रेखाचित्र के स्थान पर आव्यूह निर्मित किया जा सकता है। इसी तरीके से लोगों ने जटिल व उलझे हुए रेखाचित्रों की जानकारी को दर्शाने के लिए आव्यूह का इस्तेमाल शुरू किया था (वैसे कोनिग्सबर्ग रेखाचित्र उतना जटिल नहीं है)। कई मायनों में आव्यूह का उपयोग वास्तविक दुनिया की परिघटनाओं के प्रस्तुतीकरण में किया जा सकता है।
आव्यूह का उपयोग समय के साथ उप-परमाणविक कणों में होने वाले परिवर्तनों की व्याख्या हेतु भी किया जाता है। हाई स्कूल में इनका उपयोग युगपत समीकरणों (simultaneous equations) के हल हेतु किया जाता है। इन समीकरणों में दो या दो से अधिक अज्ञात राशियाँ होती हैं। दरअसल, आव्यूह इतना शक्तिशाली औज़ार है कि इनकी मदद से कई अज्ञात राशियों (20, 30 तक अज्ञात राशियों) वाली युगपत समीकरणों को हल कर सकते हैं।
तो ऐसा रहा आव्यूह से परिचय। क्या बात है! पहली बार मैंने देखा कि गणित में कोई विषय कैसे उभरता है। अच्छा लगा। भले ही हमने इस पर आगे काम नहीं किया, किन्तु मैं यह जानकर खुश था कि गणित के किसी भी विचार के पीछे कोई कारण होता है। ऐसा नहीं है कि विचार आसमान से टपककर हमारी पाठ्यपुस्तकों में छप जाते हों। मेरा खयाल है कि यदि आप क्यों का जवाब देने के लिए किसी मामले की जड़ में जाएँ, तो सीखना ज़्यादा उद्देश्यपूर्ण हो जाता है।
हमने कोनिग्सबर्ग की समस्या में सात पुलों को पार करने के विभिन्न रास्ते टटोलते हुए दो कक्षा-सत्र बिताए और अन्तत: असफल रहे। तब चन्ना ने हमें बताया कि ओइलर ने दर्शाया था कि कोनिग्सबर्ग समस्या को कभी हल नहीं किया जा सकता। आँखों में वही जानी-पहचानी चमक लिए, चन्ना ने बताया कि ओइलर ने अपना प्रमाण कागज़-पेंसिल की मदद से दिया था, पुलों को पार करने की कोशिश तक नहीं की थी। चन्ना ने कहा कि यही गणित की शक्ति है।
चन्ना ने हमें बताया था कि गणित के इस नए विषय ‘ग्राफ सिद्धान्त’ और उससे सम्बन्धित आव्यूह के विचार का विकास गणित की एक अन्य शाखा ‘टोपोलॉजी’ यानी स्थलाकृति-विज्ञान के पहले हुआ था। समय के अभाव के चलते वे इनकी कड़ियों पर ज़्यादा रोशनी नहीं डाल पाए थे और न ही हमारे पास इतना समय था कि हम यह देख पाते कि वास्तव में ओइलर ने कोनिग्सबर्ग समस्या को कैसे सुलझाया था। जैसा कि मुझे बाद में पता चला, प्रमाण समझना बहुत मुश्किल न था, लेकिन ओइलर के ज़माने में यह ज़रूर सुर्खियों में रहा होगा। कुछ गणितज्ञ कहते हैं कि कोनिग्सबर्ग समस्या ओइलर का सबसे मशहूर काम था क्योंकि इसने आम लोगों का ध्यान खींचा, हालाँकि यह उनकी सबसे गहरी उपलब्धि कदापि नहीं थी।
चन्ना के साथ हमारी रोमांचक यात्राएँ जारी रहीं, आई.सी.एस.ई. (इंडियन सार्टिफिकेट ऑफ सेकंडरी एजूकेशन) के रूखे-सूखे पाठ्यक्रम से कहीं आगे तक। गणित के प्रति मेरा आकर्षण बढ़ता ही गया।
नक्शों में रंग
चन्ना ने बताया कि पहले-पहले तो ग्राफ सम्बन्धी ओइलर के विचारों (जो कोनिग्सबर्ग पहेली में से उभरे थे) का उपयोग मात्र मनोरंजक गणित में पहेलियाँ सुलझाने और खेलों में किया गया। लेकिन ज्ञान की साधना में अक्सर ऐसे जुड़ाव उजागर होते हैं, जिनके बारे में आपने सोचा भी नहीं था। धीरे-धीरे यह समझ में आया कि ग्राफ के विचार को इस क्षेत्र की कई अन्य समस्याओं पर लागू किया जा सकता है। जैसे चार रंगों की समस्या (Four-Colour Problem - FCP) जिसे कभी-कभी चार रंग प्रमेय भी कहते हैं। इस तरह चन्ना हमें गणित की एक और मशहूर तहकीकात की ओर ले गए थे। बौद्धिक संघर्ष और खोजों को लेकर और अधिक दिलचस्प चर्चा हुई। काश, परीक्षाएँ न होतीं।
FCP को केनेथ एप्पल और वोल्फगैंग हाकेन ने सुलझाया था। और वह भी 1978 में बाल्डविन्स में मेरे प्रवेश से मात्र दो वर्ष पहले। इस पहेली की शुरुआत नक्शानवीसी और मानचित्रण में से हुई थी और यह 1852 से 1976 तक यानी पूरे 124 सालों तक अनसुलझी रही। यह एक मासूम सवाल से शुरू हुई थी जो यूनिवर्सिटी कॉलेज, लंदन के एक विद्यार्थी फ्रांसिस गुथ्री ने 1852 में कभी अपने भाई से पूछा था। जिज्ञासावश गुथ्री ने पूछा था कि क्या किसी नक्शे में इस तरह रंग भरे जा सकते हैं कि किन्हीं भी दो सटे हुए इलाकों का रंग समान न हो। यह सवाल शायद उसके मन में तब आया था जब वह इंग्लैंड के नक्शे में रंग भर रहा था। पता नहीं वह नक्शे में रंग क्यों भर रहा था, किन्तु कई बार एकदम निरापद गतिविधि भी चीज़ों के कामकाज के तौर-तरीकों के बारे में गहरी सूझबूझ प्रदान कर सकती है। खैर, फ्रांसिस को तो यह भान भी न होगा कि उसका यह सवाल गणित की दुनिया में भूचाल ला देगा। अन्तत: इस पहेली को जिस ढंग से सुलझाया गया, गुथ्री बन्धुओं ने उसकी कल्पना तक न की होगी। FCP का कोई आसान कागज़-पेंसिल हल नहीं है जिसका सत्यापन कोई भी कर सके। यह पहली बार था कि गणित के एक प्रमुख प्रमेय को ‘सिद्ध’ करने के लिए सुपरकम्प्यूटर का उपयोग किया गया। सुपरकम्प्यूटर की ज़रूरत आँकड़ों के विशाल ज़खीरे के प्रोसेसिंग के लिए पड़ी। इतनी भारी मात्रा में आँकड़े उत्पन्न करना इसलिए ज़रूरी था क्योंकि पहले ‘n’ क्षेत्रों वाले नक्शों में छोटे विन्यासों को देखने की कोशिश की गई और फिर यह देखा गया कि क्या यह मान्यता सही है कि चार रंग इस काम के लिए पर्याप्त हैं। ‘n’ क्षेत्रों वाले नक्शे में विन्यासों की बड़ी संख्या हो सकती है।
अन्तत: इस पहेली को जिस ढंग से सुलझाया गया, गुथ्री बन्धुओं ने उसकी कल्पना तक न की होगी। FCP का कोई आसान कागज़-पेंसिल हल नहीं है जिसका सत्यापन कोई भी कर सके। यह पहली बार था कि गणित के एक प्रमुख प्रमेय को ‘सिद्ध’ करने के लिए सुपरकम्प्यूटर का उपयोग किया गया। सुपरकम्प्यूटर की ज़रूरत आँकड़ों के विशाल ज़खीरे के प्रोसेसिंग के लिए पड़ी। इतनी भारी मात्रा में आँकड़े उत्पन्न करना इसलिए ज़रूरी था क्योंकि पहले ‘n’ क्षेत्रों वाले नक्शों में छोटे विन्यासों को देखने की कोशिश की गई और फिर यह देखा गया कि क्या यह मान्यता सही है कि चार रंग इस काम के लिए पर्याप्त हैं। ‘n’ क्षेत्रों वाले नक्शे में विन्यासों की बड़ी संख्या हो सकती है।
गणित समुदाय में इस बात को लेकर बहस चली थी कि क्या कम्प्यूटर-सहायित विधि गणितीय प्रमाण माना जा सकता है। गणित युक्लिड की शैली में तर्क पर आधारित निगमनात्मक प्रमाण का उपयोग करता है जबकि यह तो एक प्रायोगिक प्रमाण जैसा था जिसका उपयोग आम तौर पर प्राकृतिक विज्ञान में किया जाता है।
सरल शब्दों में कहें, तो FCP का वक्तव्य यह है कि किसी नक्शे मेंे इस तरह रंग भरने के लिए चार रंग पर्याप्त हैं ताकि किन्हीं भी दो सटे हुए क्षेत्रों का रंग एक ही न रहे। मेरा खयाल है, इसे समझना आसान है और यह सरलता का धोखा पैदा करती है।
एक ज़्यादा गहन वक्तव्य शायद ऐसा दिखेगा:
“किसी तल का सटे हुए क्षेत्रों में विभाजन, जिससे आपको नक्शा नामक चित्र प्राप्त होता है, में नक्शे के क्षेत्रों में रंग भरने के लिए, ताकि किन्हीं भी दो सटे हुए क्षेत्रों का रंग एक न हो, चार से अधिक रंगों की ज़रूरत नहीं होगी।”
चित्र-5 में दर्शाए गए सरल नक्शे में इस तरह रंग भरने के लिए, ताकि किन्हीं भी सटे हुए क्षेत्रों का रंग एक ही न हो, चार रंगों की ज़रूरत है। यह हमें सामान्य नक्शों जैसा नहीं दिखता क्योंकि यह सीधी रेखाओं वाली ज्यामितीय आकृतियों से बना है। बहरहाल, यह है तो नक्शा ही।
हालाँकि, गणितज्ञ इस बात को पाँच रंगों के सन्दर्भ में सिद्ध कर पाए थेे, लेकिन FCP एक सदी से भी ज़्यादा समय तक समाधान का मुँह चिढ़ाती रही। रोचक है, नहीं? हम कभी नहीं कह सकते कि मानव क्रियाकलापों का कौन-सा क्षेत्र ज्ञान के किसी नए क्षेत्र का पालना बनेगा, जिस पर लोग वर्षों बाद काम करेंगे। तो उस सारे नाटक के बाद हम अब जानते हैं कि चार रंग पर्याप्त हैं, चाहे नक्शा कितना भी जटिल हो, समतल सतह पर हो या गोलाई वाली सतह पर।
इसे करके देखिए। भारत का एक राजनैतिक नक्शा लीजिए जिसमें रंग न भरे हों (जिसमें राज्यों की सीमाएँ स्पष्ट दर्शाई गई हों)। बच्चे होमवर्क इसी पर करते हैं। हर राज्य में एक अलग रंग भरिए: देखिए कि क्या आप यह काम तीन, चार या पाँच रंगों से कर सकते हैं, इस शर्त का पालन करते हुए कि किन्हीं भी सटे हुए राज्यों में एक ही रंग न भरा जाए। FCP का एहसास बना? यह बहुत सरल दिखता है लेकिन इसे हत्थे चढ़ने में एक सदी से ज़्यादा वक्त लगा था।
तो, चन्ना ने हमें गणित एक्सप्रेस में सवारी कराई। वे हमेशा कहानियों से कक्षा में जान फूँक देते थे और हमें याद दिलाते थे कि पाठ्यक्रम में जितना दिया गया है, गणित सीखना उससे कहीं ज़्यादा है। शायद ज़्यादा दिलचस्प हिस्से तो पाठ्यक्रम से बाहर ही हैं। 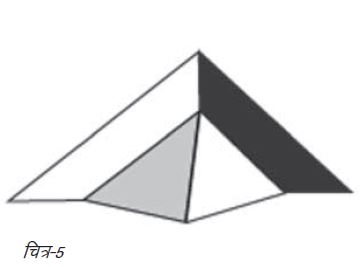 हज्जाम की दुविधा
हज्जाम की दुविधा
महीने बीतते रहे। हम घूमते-घामते सेट थियरी (समुच्चय सिद्धान्त) में पहुँचे। और चन्ना की कहानियाँ और रहस्यमय हो गईं। कभी-कभी तो वे प्रहसन भी लगती थीं। समुच्चय की मानक परिभाषा के ढर्रे तक पहुँचने से पहले चन्ना ने एक दिन घोषणा की, “चलो, मैं तुम्हें एक गाँव के एक हज्जाम की कहानी सुनाता हूँ।”
हज्जाम? हमने उम्मीद से उनकी ओर देखा। “मान लो, किसी गाँव में एक हज्जाम है, जो उन सबकी और सिर्फ उन बाशिंदों की हजामत करता है जो खुद की हजामत नहीं करते। तो हज्जाम खुद की हजामत करता है या नहीं करता?”
चलिए, इसके बारे में थोड़ा सोचते हैं। हज्जाम ऐसे किसी बाशिन्दे की हजामत नहीं करता जो खुद की हजामत करता हो। वह सिर्फ उन बाशिन्दों की हजामत करता है जो खुद की हजामत नहीं करते। लेकिन इस सवाल का जवाब देने में आप उलझन में फँस जाते हैं कि हज्जाम की हजामत कौन करता है।
यदि वह खुद की हजामत करे, तो नियम का क्या होगा कि वह ऐसे किसी शख्स की हजामत नहीं करता जो खुद की हजामत करता हो। लेकिन यदि वह खुद की हजामत न करे, तो वह उन बाशिन्दों में से एक होगा जो खुद की हजामत नहीं करते। तब नियम के मुताबिक उसे खुद की हजामत करनी चाहिए।
लीजिए, यह रहा एक विरोधाभास। इसे पचाने में थोड़ा वक्त लगता है। पहली नज़र में तो समस्या आसान लगती है, लेकिन जब इसमें घुसेंगे तो मामला उलझता ही जाएगा। जब कक्षा में इसकी चर्चा हुई थी, तो मुझे याद है कि मैं एक ऐसे हज्जाम की कल्पना करता रहा था जिसकी दाढ़ी बढ़ती ही जा रही है - बढ़ती का नाम दाढ़ी। “हजामत करे या न करे?” बेचारे हज्जाम ने यह सवाल हज़ारों-लाखों बार पूछा होगा।
बहरहाल, हमें इस हज्जाम की दुविधा का सामना करके मज़ा आया था। चन्ना ने बताया था कि यह ‘हज्जाम की दुविधा’ के नाम से मशहूर है। इसे सबसे पहले गणितज्ञ और दार्शनिक बरट्रैंड रसेल ने बीसवीं सदी की शुरुआत में प्रस्तुत किया था। मुझे याद है कि कक्षा में इस विरोधाभास को लेकर ज़ोर-ज़ोर-से तर्क-वितर्क हुए थे। लेकिन हम इससे निपट नहीं सके थे।
‘विरोधाभास’ शब्द से हमारा पहला परिचय इसी तरह हुआ था। हममें से किसी को पता नहीं था कि यह प्राणि है क्या बला। चन्ना ने समझाया कि गणित में विरोधाभास तब होता है जब हमारे सामने कोई ऐसा कथन आता है जिसमें ऐसे विचार होते हैं जो सत्य लगते हैं, लेकिन परस्पर विरोधी होते हैं (एक-दूसरे को काटते हैं)। उदाहरण के लिए निम्नलिखित दो कथनों पर गौर कीजिए:
“इस वाक्य में सात शब्द नहीं हैं।” जबकि वास्तव में इसमें सात शब्द हैं।
“इस वाक्य में सात शब्द हैं।” जबकि दरअसल इसमें छ: शब्द ही हैं।
विरोधाभास का अर्थ समझने का यह आसान तरीका है। ये वाक्य खुद अपना खण्डन करते हैं। इन वाक्यों का अस्तित्व ही कैसे हो सकता है? लेकिन इनका अस्तित्व है, हमारा मुँह चिढ़ाते हुए। इसे ही विरोधाभास कहते हैं।
हज्जाम के विरोधाभास के कई विविध रूप हैं और इसे ‘आत्म-सन्दर्भ का विरोधाभास’ या ‘पैराडॉक्स ऑफ सेल्फ रेफरेंस’ भी कहते हैं। गणित के कई विरोधाभास इस श्रेणी में आते हैं। चन्ना ने बताया था कि हज्जाम का विरोधाभास गणित की ‘समुच्चय सिद्धान्त’ नामक शाखा के केेन्द्र में उपस्थित विरोधाभास को उजागर करता है। वे चाहते थे कि हम समझें कि समुच्चय का विषय एक ऐसा विषय है जो गणित के विकास के कुछ सबसे तल्ख विरोधाभास और संघर्ष का गवाह रहा है।
सरल शब्दों में, विरोधाभास का मतलब है कि कोई ऐसा वक्तव्य ‘S’ होता है कि ‘S’ और उसका खण्डन (‘S नहीं’) दोनों सत्य होते हैं (जैसा कि हमने हज्जाम के मामले में देखा था)। ऐसी असंगतियाँ पूरे विषय की बुनियाद को थोड़ा ढुलमुल बना देती हैं, क्योंकि तब हमारे पास किसी भी गणितीय प्रमाण पर भरोसा करने का कोई आधार नहीं होता।
याद करें जब हमने त्रिभुज प्रमेय तथा उसके प्रमाण की चर्चा की थी; चन्ना का आग्रह था कि प्रमाण ठोस व मज़बूत होना चाहिए, बात चाहे किसी भी किस्म के त्रिभुज की हो। हज्जाम के विरोधाभास जैसे आत्म-सन्दर्भ वाले विरोधाभासों को समझने के लिए, इस विरोधाभास के उस संस्करण पर विचार कीजिए जिसे ‘झूठे का विरोधाभास’ कहते हैं (मुझे याद है, चन्ना ने इसकी भी बात की थी): “सारे क्रीटवासी झूठे होते हैं।” इस प्राचीन विरोधाभास का श्रेय एपिमेनिड्स को दिया जाता है, जो स्वयं क्रीटवासी थे। वे ईसा पूर्व छठी या सातवीं सदी में क्रीट में रहते थे।
हज्जाम के विरोधाभास जैसे आत्म-सन्दर्भ वाले विरोधाभासों को समझने के लिए, इस विरोधाभास के उस संस्करण पर विचार कीजिए जिसे ‘झूठे का विरोधाभास’ कहते हैं (मुझे याद है, चन्ना ने इसकी भी बात की थी): “सारे क्रीटवासी झूठे होते हैं।” इस प्राचीन विरोधाभास का श्रेय एपिमेनिड्स को दिया जाता है, जो स्वयं क्रीटवासी थे। वे ईसा पूर्व छठी या सातवीं सदी में क्रीट में रहते थे।
या निम्नलिखित वक्तव्य पर गौर कीजिए: “यह कथन असत्य है।” क्या यह कथन सत्य है? इस कथन को सत्य होने के लिए वास्तव में इसे असत्य होना पड़ेगा। और यदि यह कथन असत्य है, तो यह सत्य है। इसमें ज़रूर कुछ पागलपन है।
हज्जाम के विरोधाभास के समान उपरोक्त सारे कथनों की परिणति विरोधाभास में होती है। ज़रा सोचिए इनके बारे में! खप जाइए। ये विरोधाभास आपके सिर पर सवार हो जाएँगे। पता नहीं किसने सोचा था कि गणित में ऐसे सारे सनकी पेंच-ओ-खम होते हैं। विरोधाभासों को लेकर हमारी हर गर्मागरम चर्चा के बाद चन्ना पूरी कक्षा का मुआयना करते। आम तौर पर उनके मुँह पर सन्तोष की एक मुस्कराहट होती जो सिर्फ उस शिक्षक के नसीब में होती है जिसने सीखने वालों में और ज़्यादा सीखने की ललक पैदा कर दी हो।
मुझे बाद में पता चला कि विद्वान ऑस्ट्रियन-अमरीकी तर्कवादी और दार्शनिक कुर्ट गोडेल ने आत्म-सन्दर्भ विरोधाभासों के आधार पर यह दर्शाया था कि गणित ‘अपूर्ण’ है और सदा ‘अपूर्ण’ ही रहेगा। यदि गणित सचमुच अपूर्ण है, तो विज्ञान के बारे में क्या कहा जाए, जिसकी रीढ़ ही गणित से बनी है? तब क्या हम यह कह सकते हैं कि विज्ञान से जो ज्ञान हमें प्राप्त होता है, वह हमेशा अपूर्ण ही रहेगा? ये उलझाने वाले सवाल हैं। मैंने इनकी थोड़ी और चर्चा पुस्तक के अन्तिम हिस्से में अतिरिक्त नोट्स वाले खण्ड में की है।
अनन्त चर्चा
इसके बाद हमने थोड़ी चर्चा अनन्त के बारे में की। यह भी समुच्चयों के सन्दर्भ में ही हुई थी। मुझे याद है चन्ना ने थोड़ा मनहूस अन्दाज़ में कहा था, “अनन्त कोई संख्या नहीं है, क्योंकि यदि यह कोई संख्या होती तो आप इसमें एक जोड़कर अगली संख्या पर विचार करने लगते। यह सिलसिला तो अन्तहीन ढंग से चल सकता है और हमें हर बार सुपरिभाषित संख्याएँ मिलती जाएँगी। इसलिए, हम अनन्त को एक संख्या मानकर अंकगणित की सामान्य संक्रियाओं का उपयोग करके उसे नहीं सम्भाल सकते।”
इस बात ने मुझे काफी हैरान किया। यदि अनन्त कोई संख्या नहीं है, तो फिर अनन्त का चक्कर क्या है? हम इससे कैसे निपटेंगे? अनन्त की चर्चा के दौरान समुद्र तट पर रेत के कणों की संख्या की बात उठी थी। उनकी संख्या निश्चित (सान्त) है या अनन्त? मेरा ख्याल है कि हमारी चर्चा में यह बात उठी थी कि अनन्त क्या हो सकता है और क्या नहीं। मैं उन छात्रों में था जिनका तर्क था कि समुद्र तट पर रेत के कणों की संख्या अनन्त है जबकि अन्य कुछ का कहना था कि वह निश्चित है। मेरा तर्क यह था कि सिद्धान्तत: रेत के हरेक कण को अनन्त रूप से तोड़ा जा सकता है। तब कणों की संख्या निश्चित कैसे हो सकती है? आपको क्या लगता है?  अनन्त के बारे में चकराने वाली बात यह थी कि इसे किसी अन्य संख्या के रूप में नहीं देखा जा सकता है। मामला और भी रोचक हो गया जब चन्ना ने बताया कि “अनन्त की अलग-अलग कोटियाँ होती हैं।” उदाहरण के लिए, संख्याओं का कौन-सा समुच्चय ज़्यादा बड़ा है - सारी सम संख्याओं का समुच्चय या सारी प्राकृतिक संख्याओं का समुच्चय? संख्याओं के ये दोनों समुच्चय अनन्त हैं, लेकिन क्या हम कह सकते हैं कोई एक-दूसरे से ज़्यादा बड़ा या ज़्यादा अनन्त है? क्या अनन्त समुच्चयों की तुलना का कोई तरीका है?
अनन्त के बारे में चकराने वाली बात यह थी कि इसे किसी अन्य संख्या के रूप में नहीं देखा जा सकता है। मामला और भी रोचक हो गया जब चन्ना ने बताया कि “अनन्त की अलग-अलग कोटियाँ होती हैं।” उदाहरण के लिए, संख्याओं का कौन-सा समुच्चय ज़्यादा बड़ा है - सारी सम संख्याओं का समुच्चय या सारी प्राकृतिक संख्याओं का समुच्चय? संख्याओं के ये दोनों समुच्चय अनन्त हैं, लेकिन क्या हम कह सकते हैं कोई एक-दूसरे से ज़्यादा बड़ा या ज़्यादा अनन्त है? क्या अनन्त समुच्चयों की तुलना का कोई तरीका है?
मैंने काफी बाद में जाना कि संख्या रेखा पर किन्हीं भी दो बिन्दुओं के बीच ‘वास्तविक संख्याएँ’ (जिनमें पूर्णांक संख्याएँ, भिन्न या परिमेय संख्याएँ और अपरिमेय संख्याएँ शामिल हैं) ‘प्राकृतिक संख्याओं’ (हमारे द्वारा गिनती के लिए इस्तेमाल की जाने वाली संख्याएँ, जैसे 1, 2, 3 वगैरह) के समुच्चय से ज़्यादा होती हैं। यह थोड़ा उलझाने वाला है, नहीं? जर्मन गणितज्ञ और समुच्चय सिद्धान्त के संस्थापक जॉर्ज कैंटर ने प्रमाण के आधार पर दर्शाया था कि प्राकृतिक संख्याओं की अपेक्षा वास्तविक संख्याएँ उच्चतर श्रेणी का अनन्त समुच्चय हैं। उनके इस प्रमाण को प्राय: गणित का सबसे सुरुचिपूर्ण प्रमाण कहा जाता है।
कैंटर ने यह विचार प्रस्तुत किया था कि अनन्त शब्दश: अलग-अलग आकार का हो सकता है। दरअसल, उन्होंने ‘अनन्तों की अनन्तता’ का दावा किया था! ऐसे विचार प्रस्तावित करने के लिए उन्हें साथी गणितज्ञों के तीखे, कभी-कभी निन्दात्मक, विरोध का सामना करना पड़ा था। कई गणितज्ञ तो अनन्त के विचार के साथ जूझने को लेकर भयाक्रान्त हो जाते थे। ऐसे गणितज्ञों में सबसे मशहूर थे हेनरी पॉइनकेयर, जिन्होंने कैंटर के काम को गणित को ग्रस्त करने वाली ‘गम्भीर बीमारी’ की संज्ञा दी थी। अलबत्ता, कैंटर के विचारों ने उनके समकालीन गणितज्ञों को अनन्त को सम्भालने का एक औज़ार प्रदान किया था।
फर्मा का अन्तिम प्रमेय
और अन्त में, बिग बी - ‘फर्मा के अन्तिम प्रमेय’ को कौन भूल सकता है? हम चन्ना की कक्षा में पायथागोरस प्रमेय के प्रमाण की चर्चा कर रहे थे: कि किसी समकोण त्रिभुज के विकर्ण का वर्ग शेष दो भुजाओं के वर्गों के योग के बराबर होता है। अर्थात a2 + b2 = c2 जहाँ a और b समकोण त्रिभुज की दो भुजाएँ हैं और c विकर्ण है। (याद है लीलावती में भास्कराचार्य की पहेली, जिसके हल के लिए पायथागोरस प्रमेय का उपयोग किया जाता है?)
वैसे पक्का कहना मुश्किल है मगर आखिरी गिनती तक पायथागोरस प्रमेय के पूरे 367 अलग-अलग प्रमाण थे! ‘अलग-अलग’ शब्द का उपयोग कर रहा हूँ क्योंकि कोई प्रमाण गिनती में तभी शामिल होता है जब वह बाकी सारे प्रमाणों से अलग हो। शुरुआती बीसवीं सदी के एक प्रोफेसर एलिशा स्कॉट लूमिस ने अपनी पुस्तक पायथागोरियन प्रपोज़िशन (पायथागोरस प्रस्तावना) में इन 367 प्रमाणों का संकलन प्रस्तुत किया है। आश्चर्यजनक बात यह है कि एक ही सत्य को स्थापित करने के इतने अलग-अलग तरीके हैं। इस सूची में भास्कर द्वारा प्रस्तुत दृश्य प्रमाण भी है। बताते हैं कि प्रमाण का चित्र दिखाते हुए उन्होंने कहा था, ‘देखो’। इस प्रमाण के लिए उन्हें किसी शाब्दिक विवरण की ज़रूरत नहीं पड़ी थी।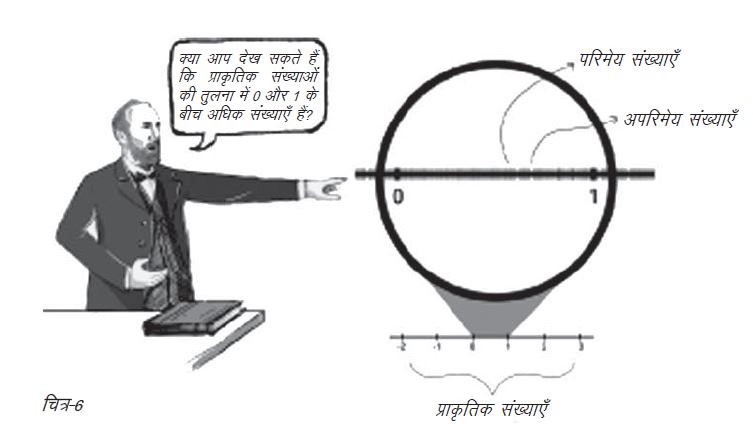 हाई स्कूल का हर बच्चा पायथागोरस प्रमेय जानता है मगर सम्भवत: उनमें से कई छात्र प्रमेय के आगे नहीं गए होंगे। खैर, चन्ना ने ठीक यही किया। हमें फर्मा के अन्तिम प्रमेय (FLT) की दावत दी गई जो पूरे 348 साल तक अनसुलझी पड़ी रही थी। तो FLT है क्या? कहानी कुछ यों है कि पियरे डी फर्मा नाम के एक भले फ्रांसीसी, जो पेशे से वकील थे, और गणित जिनका शौक था, 1650 ईस्वी के आसपास ‘पायथागोरस तिकड़ियों’ पर विचार कर रहे थे।
हाई स्कूल का हर बच्चा पायथागोरस प्रमेय जानता है मगर सम्भवत: उनमें से कई छात्र प्रमेय के आगे नहीं गए होंगे। खैर, चन्ना ने ठीक यही किया। हमें फर्मा के अन्तिम प्रमेय (FLT) की दावत दी गई जो पूरे 348 साल तक अनसुलझी पड़ी रही थी। तो FLT है क्या? कहानी कुछ यों है कि पियरे डी फर्मा नाम के एक भले फ्रांसीसी, जो पेशे से वकील थे, और गणित जिनका शौक था, 1650 ईस्वी के आसपास ‘पायथागोरस तिकड़ियों’ पर विचार कर रहे थे।
पहले संख्याओं के ऐसे समूहों के उदाहरण दे देता हूँ जिन्हें पायथागोरस तिकड़ी की संज्ञा दी गई है। {3, 4, 5}, {5, 12, 13} वगैरह पायथागोरस तिकड़ियाँ हैं क्योंकि 32 + 42 = 52 और 122 + 52 = 132। ऐसी तिकड़ियाँ बनाने के कई तरीके हैं। मसलन, हम ऐसी तिकड़ी की सभी संख्याओं में 2 जैसी किसी एक संख्या का गुणा करके नई तिकड़ी प्राप्त कर सकते हैं। जैसे {3, 4, 5} में 2 का गुणा करने पर हमें प्राप्त होगा {6, 8, 10}और यह आसानी-से देखा जा सकता है कि 62 + 82 = 102। ज्यामितीय दृष्टि से देखें तो इसका मतलब होता है कि हम एक ऐसा समकोण त्रिभुज बना सकते हैं जिसकी भुजाओं की लम्बाइयाँ 6, 8 व 10 इकाई होगी और विकर्ण की लम्बाई 10 इकाई होगी। आप इस तिकड़ी को 2 से गुणा कर दीजिए और एक और तिकड़ी प्राप्त हो जाएगी। ऐसा अन्तहीन ढंग से किया जा सकता है। ऐसी तिकड़ियाँ प्राप्त करने के अन्य तरीके भी हैं।
धीरे-धीरे चन्ना हमें कहानी के पेंच तक ले गए। उन्होंने बताया कि फर्मा ने सरल-सा सवाल पूछा था, जो शायद ऐसा कुछ रहा होगा: “क्या यही क्रिया घनों के साथ भी की जा सकती है - अर्थात क्या हम ऐसी तीन संख्याएँ ‘a’, ‘b’ और ‘c’ खोज सकते हैं ताकि a3 + b3 = c3 हो?” वे तो मात्र एक पैटर्न ढूँढ़ रहे थे। याद रखें, गणित सीखने का एक अच्छा पैमाना यह है कि छात्र अन्तर्निहित सम्बन्ध और पैटर्न ढूँढ़ने में रुचि और काबिलियत हासिल कर ले। यह एक गणितज्ञ के स्वभाव की भी कसौटी है।
यह बात हमारे सहजबोध के खिलाफ जाती है कि n = 3 होने पर यह काम नहीं करता। शायद हमें लगा होगा कि यदि किसी समकोण त्रिभुज की दो भुजाओं पर बने वर्ग उसके विकर्ण पर बने बड़े वर्ग में समा सकते हैं तो यह चीज़ ठोस घनों पर भी लागू होनी चाहिए। जब बात घन की होती है तो हम तीसरी घात की बात कर रहे हैं (जैसे a3)। घन एक त्रि-आयामी वस्तु है जो छ: वर्गाकार फलकों से घिरी है जो एक-दूसरे से समकोण पर स्थित हैं।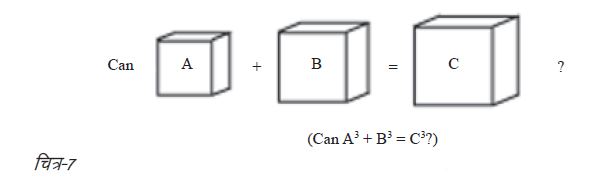 चित्र-7 में A3 को एक घन माना जा सकता है जिसकी एक भुजा A इकाई की है। इसी प्रकार से, B3 और C3। किसी A भुजा वाले घन का आयतन (A x A x A) या A3 होता है। यही स्थिति B और C भुजा वाले घनों की भी होगी। तो जब हम यह सिद्ध करने की कोशिश करते हैं कि तीन ऐसी पूर्णांक संख्याएँ A, B और C होंगी कि A3 + B3 = C3 हो, तो हम इस सवाल की कल्पना ज्यामितीय दृष्टि से कुछ इस तरह कर सकते हैं: दो घन A और B, एक तीसरे बड़े घन C में ठीक-ठीक समा जाएँ (मानकर कि वह घन खोखला है)। लेकिन गणित प्राय: सहजबुद्धि के विपरीत चला जाता है। पता यह चलता है कि A3 + B3 = C3 सही नहीं बैठता!
चित्र-7 में A3 को एक घन माना जा सकता है जिसकी एक भुजा A इकाई की है। इसी प्रकार से, B3 और C3। किसी A भुजा वाले घन का आयतन (A x A x A) या A3 होता है। यही स्थिति B और C भुजा वाले घनों की भी होगी। तो जब हम यह सिद्ध करने की कोशिश करते हैं कि तीन ऐसी पूर्णांक संख्याएँ A, B और C होंगी कि A3 + B3 = C3 हो, तो हम इस सवाल की कल्पना ज्यामितीय दृष्टि से कुछ इस तरह कर सकते हैं: दो घन A और B, एक तीसरे बड़े घन C में ठीक-ठीक समा जाएँ (मानकर कि वह घन खोखला है)। लेकिन गणित प्राय: सहजबुद्धि के विपरीत चला जाता है। पता यह चलता है कि A3 + B3 = C3 सही नहीं बैठता!
वैसे, संख्याओं की एक तिकड़ी है जो यह सिद्ध करने के बहुत करीब पहुँच जाती है कि A3 + B3 = C3 सत्य है - {12, 10, 9}। (103 + 93) का हिसाब लगाइए। यह 1729 आता है जो ‘रामानुजन संख्या’ के काफी करीब है। और 123 का मान आता है 1728, बहुत नज़दीक है न? क्रिकेट में कहते हैं न, एल.बी.डब्लू. का बहुत नज़दीकी मामला!
जब बात n = 2 (जैसे यहाँ पायथागोरस प्रमेय है) या n = 3 की हो तो हम इसकी कल्पना दृश्य रूप में कर सकते हैं। लेकिन जब बात n = 4, 5, 6... पर पहुँच जाए तो दृश्य बिम्ब के रूप में उसकी कल्पना कैसे करेंगे? तब हम मदद के लिए दो या तीन-आयामी वस्तुओं में पनाह नहीं ले सकते जिसके हम रोज़मर्रा के जीवन में आदी हैं। इस पड़ाव पर आकर चीज़ें अमूर्त हो जाती हैं और आपको सवाल को देखने के नए व अलग तरीके ढूँढ़ना पड़ते हैं। लेकिन गणितज्ञ तब तक चैन से नहीं बैठ सकते जब तक कि वे इस बात का ठोस प्रमाण न विकसित कर लें कि फर्मा की प्रमेय सारे ‘n’ के लिए सत्य नहीं है, जहाँ ‘n’ कोई धनात्मक पूर्णांक संख्या है और n>2 है। गणितज्ञ भौतिक विश्व की सीमाओं से बँधे नहीं होते और ‘n’ आयामों में काम करना उनके लिए आम बात है।
लेकिन गणितज्ञ तब तक चैन से नहीं बैठ सकते जब तक कि वे इस बात का ठोस प्रमाण न विकसित कर लें कि फर्मा की प्रमेय सारे ‘n’ के लिए सत्य नहीं है, जहाँ ‘n’ कोई धनात्मक पूर्णांक संख्या है और n>2 है। गणितज्ञ भौतिक विश्व की सीमाओं से बँधे नहीं होते और ‘n’ आयामों में काम करना उनके लिए आम बात है।
चन्ना ने बताया था कि फर्मा पूछते गए थे: क्या हम इसे चौथी घात के लिए कर सकते हैं, यानी क्या हम ऐसी ‘a’, ‘b’ और ‘c’ संख्याएँ खोज सकते हैं ताकि a4 + b4 = c4 सही बैठे? अन्तत: उन्होंने सवाल किया था: क्या ऐसी तीन संख्याएँ ‘a’, ‘b’ और ‘c’ हो सकती हैं जिनके लिए an + bn = cn सम्भव हो? फर्मा ने अवश्य ही ‘a’, ‘b’ और ‘c’ की विभिन्न घातों के लिए प्रमाण हासिल करने की कोशिश की होगी। बताते हैं कि उन्होंने चौथी घात के लिए नकारात्मक प्रमाण प्राप्त कर लिया था अर्थात वे सिद्ध कर पाए थे कि समीकरण a4 + b4 = c4 का अस्तित्व नहीं है। हम नहीं जानते कि क्या उन्होंने इसी प्रकार से यह भी सिद्ध किया था कि ‘a’, ‘b’ और ‘c’ की उच्चतर घातों के लिए ऐसे समीकरणों का अस्तित्व नहीं है। अलबत्ता, अन्तत: उन्होंने लैटिन में घोषणा की थी:
“Cubum autem in duos cubos, aut quadrato-quadratum in duos quadrato-quadratos, et generaliter nullam in infinitum ultra quadratum potestatem in duos eiusdem nominis fas est dividere cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet.”
हिदी में इसका अनुवाद कुछ इस तरह होगा:
“किसी घन को दो घनों में या किसी एक चौथी घात को दो छोटी-छोटी चौथी घातों में, या सामान्य रूप से दो से अधिक घात को उसी के बराबर दो घातों में बाँटना असम्भव है। मैंने इसका सचमुच अद्भुत प्रमाण खोज लिया है लेकिन यह हाशिया उसके लिए बहुत संकरा है।”
दूसरे शब्दों में, ऐसी कोई तीन पूर्णांक संख्याएँ ‘a’, ‘b’ और ‘c’ नहीं हैं जो समीकरण an + bn = cn को n का मान 2 से अधिक होने पर सन्तुष्ट कर सकें।
“मैंने इसका सचमुच अद्भुत प्रमाण खोज लिया है लेकिन यह हाशिया उसके लिए बहुत संकरा है।” यह कथन फर्मा ने एक किताब अरिथमेटिका में हाशिए पर लिखा था। यह पुस्तक तीसरी सदी के एक महान गणितज्ञ डायोफैन्टस द्वारा लिखी गई थी। फर्मा की टिप्पणी युक्त यह प्रति फर्मा के निधन के 30 साल बाद 1665 में खोजी गई थी। हम वास्तव में जानते नहीं कि वकील साहब ने प्रमाण पता कर लिया था या नहीं। कई लोगों को लगता था कि उन्होंने प्रमाण नहीं खोजा था क्योंकि FLT के प्रमाण हेतु ज़रूरी औज़ार उस समय उपलब्ध नहीं थे। शायद वास्तविकता कभी पता नहीं चलेगी।
अलबत्ता, फर्मा के कथन ने गणित की सबसे प्रख्यात समस्याओं में से एक को जन्म दिया जो लगभग साढ़े तीन सौ वर्षों तक सुलझ नहीं पाई और दुनिया भर के गणितज्ञों को चकरा दिया। हलचल इतनी अधिक थी कि FLT को प्रमाणित करने के लिए जर्मन उद्योगपति पौल वोल्फस्केल ने 1908 में 1 लाख मार्क का इनाम भी घोषित कर दिया था।
अन्तत: कहानी का समापन करते हुए चन्ना ने थोड़ा रुआँसा होकर कहा था, “शायद किसी दिन तुममें से कोई इसे सुलझाएगा।” हम उनकी निराशा को महसूस कर सकते थे।
आगे बढ़ने से पहले, मैं आपके सामने तीन-तीन संख्याओं के दो समुच्चय छोड़ूँगा, जो शायद फर्मा और उनके अन्तिम प्रमेय को झुठला सकेंगे। इनको परखिए, अपना भाग्य आज़माइए, मशहूरी पर अपना दावा जताइए और इनाम की राशि मेरे साथ बाँटिए। ये रहे वे दो समुच्चय:
पहला समुच्चय है:
398712 + 436512 = 447212
दूसरा समुच्चय है:
178212 + 184112 = 192212
मध्य 1980 का दशक FLT का रोमांचक दौर था। उस समय तक अनगिनत गणितज्ञ इस प्रमेय पर हाथ आज़मा चुके थे और अथक परिश्रम के बाद घात n के विभिन्न मानों के लिए प्रमाण प्रस्तुत किए जा चुके थे। 1980 में बाल्डविन के शताब्दी वर्ष तक 1,25,000 तक की घात (n) के लिए FLT को प्रमाणित किया जा चुका था। लेकिन धनात्मक पूर्णांक संख्याओं की अनन्तता को देखें, तो 1,25,000 कुछ नहीं है। ज़रूरत तो एक ऐसे सामान्य प्रमाण की है जो हरेक मामले में लागू हो सके। त्रिभुज के तीन कोणों के योग वाली प्रमेय का प्रमाण याद है न? जब पहली बार हमारा सामना प्रमाण की धारणा से हुआ था, तो हम बहुत जूझे थे। यह किसी भी अन्य सवाल को छुड़ाने से अलग था। और विशाल विरोधी उदाहरण (Monstrous Counter Example) एक और ऐसी ही कवायद थी।
हमें ज़रा भी अन्दाज़ नहीं था कि 1985 में जब हम कक्षा 10 में थे, तब एक ब्रिटिश गणितज्ञ एंड्रयू वाइल्स यह निर्णय लेने की कगार पर थे कि वे अपने जीवन के अगले सात-आठ साल पूरी तरह गोपनीय ढंग से FLT को तोड़ने में लगाएँगे। उस समय तक गणित की नई शाखाएँ अस्तित्व में आ चुकी थीं। वाइल्स को इनकी मदद मिली। उनका चक्करदार प्रमाण पूरे 150 पन्नों में फैला था।
पता नहीं जब 1994 में अन्तत: इस समस्या को सुलझा हुआ घोषित कर दिया गया तो चन्ना को कैसा महसूस हुआ होगा। तब उन्होंने अपने छात्रों से क्या चर्चा की होगी? वाइल्स की कहानी दिलचस्प है, किन्तु यदि मैं यहाँ उसे लेकर बैठ गया, तो हम चन्ना से दूर चले जाएँगे। कई सारी मशहूर किताबों में FLT जद्दोजहद की बात की गई है और इसका प्रमाण समझाया गया है। आप उन्हें देख सकते हैं।
FLT सारी बाधाओं के विरुद्ध मानव मस्तिष्क और जीवट की जीत की एक उम्दा मिसाल है। वाइल्स की कहानी बताती है कि एक व्यक्ति की अदम्य इच्छा क्या कुछ हासिल कर सकती है। यह मानव संघर्ष की किसी भी अन्य कहानी के बराबर ही बाँधने वाली है। यह दर्शाती है कि यदि हम अपने सपनों को साकार करने के लिए धैर्यपूर्वक लगे रहें तो सारी बाधाओं के बावजूद एक दिन हम मंज़िल पा ही लेंगे।
स्कूल के हर छात्र के लिए गणित ऐसी यात्रा की शुरुआत बन सकता है। शिक्षा का काम यह है कि ऐसे हालात तैयार करे कि हर छात्र इस सुन्दर विषय तक पहुँच बना पाए। यह काम आसान नहीं है। हमारा सामना एक सुस्थापित रटन्त विद्या की संस्कृति से है। यह एक ऐसी संस्कृति है जो विभिन्न पृष्ठभूमियों और प्राय: चुनौतीपूर्ण पृष्ठभूमियों से आने वाले छात्रों के साथ एक सामर्थ्यजनक ढंग से संवाद नहीं करती।
असीम विस्मय
चन्ना कई बारे हमें इन दिलकश पगडण्डियों पर ले गए। मैं उस विस्मय का ज़िक्र ज़रूर करूँगा जो मैंने उस समय महसूस किया था जब हमारा सामना पाई (Π) से हुआ था। पाई उस समूह का सदस्य है जिन्हें अपरिमेय संख्याएँ कहते हैं। ये ऐसी संख्याएँ हैं जो तर्कसंगत ढंग से व्यवहार नहीं करतीं और उनका भिन्न वाला हिस्सा चलता ही जाता है, चलता ही जाता है, दशमलव अंक का सिलसिला खत्म ही नहीं होता। मुझे आज भी हैरत होती है कि ऐसी संख्या हो भी सकती हैं। हमने चन्ना से जाना कि उस समय तक Π को बस में करने की कोशिशें अकल्पनीय रूप से विशाल स्तर पर पहुँच चुकी थीं। उस समय उपलब्ध सबसे तेज़ सुपरकम्प्यूटरों की मदद से यह पता चला था कि पाई वास्तव में दशमलव अंकों की एक अन्तहीन और अपुनरावर्ती धारा है। दशमलव के बाद पूरे 1.6 करोड़ अंकों तक तो यही स्थिति थी। मैं चकरा गया था। अब तो उन्होंने गणना कई खरब अंकों तक कर ली है, लेकिन फिर भी दशमलव अंक खत्म होने का नाम नहीं ले रहे हैं।
उन कक्षाओं को याद करके आज भी मेरे रोंगटे खड़े हो जाते हैं, जब हमें गणितीय यथार्थ की एक अपेक्षाकृत गहरी झलक मिली थी, जो परीक्षाएँ पास करने और चूहा-दौड़ के ढर्रे से, ‘सिलेबस पूरा करने’ के दबाव से एकदम अलग थी।
चन्ना का उद्देश्य सीधा-सादा था - हमें यह एहसास कराना कि गणित कोई मुर्दा विषय नहीं हैं बल्कि एक विकासमान मानवीय कहानी है जिसमें उन लोगों के लिए ढेर सारी दिलचस्प बातें और रोमांच है जो इसका अध्ययन करने को उत्सुक हैं। इससे भी बढ़कर उनका उद्देश्य था कि हममें से जो लोग कम उत्सुक थे या विषय के प्रति नकारात्मक रवैया रखते थे, उन्हें खोजबीन के इस सफर में जोड़े रखना।
यह सब सिलेबस में क्यों नहीं डाला जाता? सबसे बढ़िया हिस्सा तो छोड़ ही दिया गया है। मैं जानता हूँ कि मेरी यह बात सुन-सुनकर आप थक चुके होंगे, किन्तु मुझे लगता है कि इस बात को बार-बार, कई बार कहना मुनासिब है।
***
मार्च 15, 1985। हमारी दसवीं की परीक्षाएँ समाप्त हो चुकी हैं, जो मेरे लिए एक बड़ी राहत की बात है। आज ग्रेजुएशन दिवस था। बाल्डविन्स में इसे ‘कमेंसमेंट एक्सरसाइज़ेस’ यानी शुरुआती कसरत कहते हैं, गोया हमारे जीवन में कुछ नया होने जा रहा है।
हम सब लिंकन हॉल में इकट्ठे हुए। स्कूल छोड़ने वगैरह के बारे में आम भाषणों के बाद, मुझे याद है हमने एक मोमबत्ती जलाई थी और गलियारे से होकर लिंकन हॉल के बाहर आ गए थे। बाहर, ज़िन्दगी में जहाँ भी जाऊँगा बाल्डविन्स की भावना को साथ लेकर जाऊँगा। शायद यही अपेक्षा भी थी। हम सबने सूट पहने थे, नौजवान पुरुषों के समान। चन्ना ने यही कहा था। अन्ना ने इस अवसर के लिए अपना एक कोट मेरे लिए रफू करवा दिया था। मैंने सूट पहली बार पहना था।
हमने थोड़ा जल्दी डिनर किया। स्कूल की ओर से दावत थी। पहली बार मैंने स्कूल में भरपेट खाना खाया। उसके बाद गुडबाय, हाथ मिलाना, गले लगना वगैरह चला। शिक्षकों और दोस्तों को पता नहीं था कि हम फिर से कब मिलेंगे। सब कुछ पलक झपकते पूरा हो गया।
चुपचाप मैं मेन गेट की ओर गया, अपने सूट में पसीने से भीगा और जकड़ा हुआ। होसुर रोड पर भारी ट्राफिक था। लगभग अँधेरा था। सेक्शन ए के एक दोस्त ने आवाज़ दी। वह हम दोनों का एक फोटो चाहता था। हम दोनों गेट के सामने खड़े हो गए और किसी ने कैमरा क्लिक किया। पता नहीं वह फोटो अभी भी मौजूद है या नहीं। तभी यह बात मेरे मन में कौंधी - बाल्डविन्स में मेरा आखिरी दिन था यह।
मैं हक्का-बक्का-सा सायकिल चलाते हुए घर पहुँचा, सूट को बैग में ठूँसकर। इस बात का आदी होने में वक्त लगेगा कि अब कभी बाल्डविन्स नहीं जाना है।
आजी घर पर अकेली थीं। अन्ना शाम की शिफ्ट में गए थे, और अम्मा पास ही एक अस्पताल की इन्टेंसिव केयर युनिट में अपनी बढ़ी हुई शुगर से जूझ रही थीं। मैं पहले अस्पताल गया, खुदा का शुक्र था कि उनकी डायबिटीज़ अन्तत: काबू में थी।
सम्भल-सम्भलकर मैंने एक दूसरी दुनिया में कदम रखे, साथ में स्कूल की तमाम यादें थीं। जानता नहीं था कि आने वाले वर्षों में मुझ पर उनका क्या असर होने वाला है।
शेषागिरी केएम राव: यूनीसेफ, छत्तीसगढ़ में शिक्षा विशेषज्ञ हैं। प्रारम्भिक शिक्षा और बाल्यावस्था में विकास में विशेष रुचि। साथ ही, आधुनिक शैक्षिक मुद्दों पर लिखने में दिलचस्पी।
अँग्रेज़ी से अनुवाद: सुशील जोशी: एकलव्य द्वारा संचालित स्रोत फीचर सेवा से जुड़े हैं। विज्ञान शिक्षण व लेखन में गहरी रुचि।
यह लेख एकलव्य द्वारा प्रकाशित पुस्तक द मैन हू टॉट इंफिनिटी से लिया गया एक अंश है।

