सुशील जोशी [Hindi PDF, 150 kB]
भाग-4
यह सही है कि रदरफोर्ड मॉडल परमाणु और अल्फा कणों की परस्पर क्रिया की भलीभाँति व्याख्या कर देता है और गणितीय रूप से सारे अवलोकनों की सूक्ष्म व्याख्या भी पेश करता है। मगर इसमें कुछ गम्भीर दिक्कतें हैं।
कुछ आपत्तियाँ
यदि धनावेश केन्द्रक में समाया है और ऋणावेशित इलेक्ट्रॉन उसके आसपास स्थिर अवस्था में टिके हैं तो विपरीत आवेशों के बीच आकर्षण के चलते इलेक्ट्रॉनों को आकर्षित होकर केन्द्रक में गिर जाना चाहिए। मगर ऐसा होता नहीं है। परमाणु काफी टिकाऊ होते हैं। तो रदरफोर्ड मॉडल को लेकर पहली आपत्ति तो यही थी कि परमाणु जल्दी ही अन्दर धँस क्यों नहीं जाता।
इस आपत्ति को कुछ हद तक इलेक्ट्रॉन को परिक्रमा करवाकर निपटाने की कोशिश हुई। जब कोई कण परिक्रमा करता है तो उस पर एक अपकेन्द्री बल लगेगा और यह कहा गया कि धनावेशित केन्द्रक के चक्कर काटते इलेक्ट्रॉन पर लगने वाला अपकेन्द्री बल धनावेश के आकर्षण को सन्तुलित कर देता है और वे अपनी कक्षा में बने रहते हैं। तो रदरफोर्ड मॉडल यह बना कि केन्द्र में छोटा-सा धनावेशित केन्द्रक है और इलेक्ट्रॉन कुछ दूरी पर उसकी परिक्रमा कर रहे हैं। थोड़ा-थोड़ा सौर मण्डल जैसे दिख रहा है ना?
मगर यह भी दिक्कतों में फँस गया। इस बार जो दिक्कतें आईं वे प्रकाश के अध्ययन से आई थीं।
यह 1911 की बात है। उस समय तक यह पता चल चुका था कि यदि इलेक्ट्रॉन केन्द्रक का चक्कर लगा रहे हैं, तो उनमें एक त्वरण होगा और जब त्वरण होगा तो वे विकिरण उत्सर्जित करेंगे और उनकी ऊर्जा लगातार कम होती जाएगी। परमाणु यह विकिरण विद्युत-चुम्बकीय विकिरण के रूप में उत्सर्जित करते हैं। ऐसा होने पर उनकी परिक्रमा कक्षा लगातार सिकुड़ती जाएगी और थोड़ी ही देर में वे केन्द्रक में समा जाएँगे। तो यह परिक्रमा करते इलेक्ट्रॉन वाला मॉडल भी अस्थिर साबित होगा।
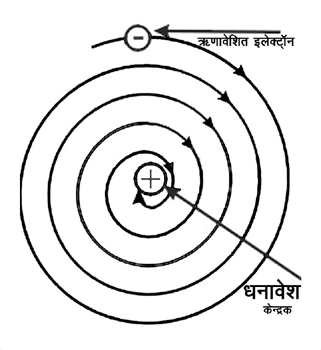परमाणु मॉडल: रदरफोर्ड मॉडल पर उठाई कुछ आपत्तियों के बाद इसमें कुछ संशोधन किए गए। इनके मुताबिक इलेक्ट्रॉन धनावेशित केन्द्रक का चक्कर लगा रहे हैं।
यह संशोधन कुछ सम्भल पाता तब तक प्रकाशिकी में हो रहे शोध से पता चला कि चक्कर लगा रहे इलेक्ट्रॉन विकिरण उत्सर्जित करेंगे। परिणाम स्वरूप इलेक्ट्रॉन की कक्षा छोटी होती जाएगी और वह केन्द्रक में समा जाएगा।
एक तीसरी समस्या भी थी। दरअसल, इसी तीसरी समस्या को सुलझाते-सुलझाते नील्स बोर परमाणु के अगले मॉडल पर पहुँचे थे। तो इस तीसरी समस्या को थोड़ा विस्तार में समझने की कोशिश करते हैं।
उस समय तक प्रकाश के वर्णक्रम का काफी अध्ययन होने लगा था। यह पाया गया था कि प्रत्येक पदार्थ का एक सुनिश्चित व अनूठा वर्णक्रम होता है। बुंसन ने अपने प्रयोगों से पदार्थों के वर्णक्रम का बढ़िया अध्ययन किया था। उन्होंने वर्णक्रम विश्लेषण के आधार पर नए तत्वों - रुबिडियम और सीज़ियम - की खोज भी कर ली थी। सूर्य के वर्णक्रम के अध्ययन के आधार पर वहाँ हीलियम की उपस्थिति का पता चल चुका था। यह सिद्धान्त विकसित हुआ था कि हरेक तत्व का वर्णक्रम उसके इलेक्ट्रॉन से उत्सर्जित विकिरण का परिणाम होता है।
यदि रदरफोर्ड का मॉडल सही है तो क्या होगा?
उत्सर्जन वर्णक्रम
रदरफोर्ड मॉडल के इलेक्ट्रॉन तो परिक्रमा कर रहे हैं और धीरे-धीरे सतत ढंग से उनके परिक्रमा पथ छोटे होते जा रहे हैं। यानी यह ऊर्जा विद्युत-चुम्बकीय विकिरण के रूप में उत्सर्जित होनी चाहिए। यदि परिक्रमा पथ का सिकुड़ना एक सतत प्रक्रिया है तो हर तरंग लम्बाई का प्रकाश निकलना चाहिए और तरंग लम्बाई लगातार कम होती जानी चाहिए।
मगर वर्णक्रम की वास्तविकता ऐसी नहीं थी। यदि किसी तत्व द्वारा उत्सर्जित प्रकाश के वर्णक्रम को देखें तो उसमें हर तरंग लम्बाई का प्रकाश नहीं होता। प्रत्येक तत्व जो वर्णक्रम देता है वह सतत नहीं बल्कि डिस्क्रीट (यानी असतत) होता है। इसका अर्थ है कि किसी भी तत्व के वर्णक्रम में कुछ तरंग लम्बाइयों का प्रकाश अनुपस्थित होता है जबकि कुछ तरंग लम्बाइयों का प्रकाश ज़्यादा होता है।
जैसे यदि किसी धातु अथवा उसके किसी यौगिक को बुंसन बर्नर की लौ में तपाएँ तो उसमें से किसी विशिष्ट रंग का प्रकाश निकलता है। मशहूर लौ परीक्षण (फ्लेम टेस्ट) इसी तथ्य पर टिका है। जैसे यदि सोडियम के किसी लवण को लौ में तपाएँ और उससे निकलने वाले प्रकाश के मार्ग में एक प्रिज़्म रखकर उसका विच्छेदन करें तो आपको एक विशिष्ट वर्णक्रम मिलेगा।
इस तरह के वर्णक्रम को परमाणु वर्णक्रम कहते हैं। इसके विस्तृत अध्ययन का काम सर्वप्रथम जे.जे. बामर (1825-1898) ने किया था। उन्होंने कम दबाव पर हाइड्रोजन से उत्सर्जित प्रकाश के वर्णक्रम पर ध्यान दिया। उन्होंने पाया कि हाइड्रोजन के वर्णक्रम में जो तरंग लम्बाइयाँ उपस्थित हैं उन्हें एक समीकरण के रूप में व्यक्त किया जा सकता है। इसके साथ ही रॉबर्ट राइडबर्ग ने भी पाया कि उत्सर्जित तरंग संख्याओं (वेव नम्बर यानी एक इकाई दूरी में कितनी तरंगें हैं) को एक समीकरण में बाँधा जा सकता है।
इस समीकरण में तरंग संख्या और थ् तरंग लम्बाई है जबकि दत् और दत्र् कोई भी दो पूर्णांक संख्याएँ हैं और ङ एक स्थिरांक है जो किसी गैस के लिए निश्चित होता है।
है ना, मज़ेदार बात। परमाणु वर्णक्रम एक पेचीदा पैटर्न होता है। जब किसी गैस को अत्यन्त कम दबाव पर एक नली में बन्द करके उच्च वोल्टेज लगाया जाए तो उसमें से प्रकाश उत्सर्जित होता है। इस प्रकाश को प्रिज़्म से विच्छेदित किया जाए तो वह विभिन्न तरंग लम्बाइयों पर रेखाओं के एक क्रम के रूप में नज़र आता है। रोचक बात यह है कि इन रेखाओं की तरंग लम्बाई को दो पूर्णांक संख्याओं से बने समीकरण की मदद से व्यक्त किया जा सकता है। 
जब भी ऐसा सरल समीकरण नज़र आए जो अवलोकनों का सटीक विवरण प्रस्तुत करने में सक्षम हो, तो यह विचार ज़रूर उभरता है कि यह समीकरण यथार्थ के किसी पहलू को व्यक्त कर रहा है।
इसी समय भौतिकी के क्षेत्र में एक और क्रान्तिकारी परिवर्तन हो रहा था। दरअसल, किसी ठोस पदार्थ को गर्म करने पर जो प्रकाश निकलता है उसके वर्णक्रम में जिन तरंग लम्बाइयों का प्रकाश नज़र आता था, उसकी तीव्रता को लेकर कुछ दिक्कतें उभरी थीं। दिक्कत यह थी विद्युत-चुम्बकीय सिद्धान्त से जिस तीव्रता की भविष्यवाणी की जाती थी, वह वास्तविक अवलोकनों से मेल नहीं खाती थी।
प्लांक की परिकल्पना
इस समस्या को सुलझाने के प्रयास में एक भौतिक शास्त्री मैक्स प्लांक ने एक परिकल्पना प्रस्तुत की थी जिसने उस ज़माने के भौतिक शास्त्रियों को चकरा दिया था और कोई भी प्लांक की बात सुनने को तैयार न था। मगर प्लांक ने जो परिकल्पना प्रस्तुत की थी वह जल्दी ही यथार्थ के हमारे चित्र में आमूल बदलाव करने वाली थी। यह परिकल्पना थी क्वांटम परिकल्पना। परिकल्पना का लब्बोलुआब यह था कि पदार्थ की तरह ऊर्जा भी निश्चित कतरों में ही पाई जाती है। इसका एक मतलब यह था कि किसी परमाणु में से ऊर्जा का विकिरण कुछ निश्चित मात्राओं में ही हो सकता है।
e=nhv
यहाँ e ऊर्जा, n कोई भी पूर्णांक संख्या, h एक स्थिरांक है और v विकिरण की आवृत्ति है।
उस समय एक और मामला प्रकाश-विद्युत प्रभाव का सामने आया था। कुछ पदार्थों पर प्रकाश डालने पर उनमें से इलेक्ट्रॉन उत्सर्जित होता है। मज़ेदार बात यह थी कि इलेक्ट्रॉन तभी उत्सर्जित होता था जब प्रकाश की आवृत्ति एक निश्चित ऊर्जा की होती थी। इससे कम ऊर्जा वाला प्रकाश चाहे कितनी भी मात्रा में दिया जाए, इलेक्ट्रॉन उत्सर्जन नहीं होता था। आइंस्टाइन ने इसका कारण क्वांटम परिकल्पना के आधार पर ही दिया था।
धीरे-धीरे यह स्वीकार किया जाने लगा था कि क्वांटम परिकल्पना शायद परमाणविक जगत का एक सामान्य सिद्धान्त है।
रदरफोर्ड के परमाणु मॉडल की दिक्कतों का समाधान तभी निकला जब क्वांटम सिद्धान्त को उनके मॉडल पर लागू किया गया। और यह काम किया था नील्स बोर ने।
सुशील जोशी: एकलव्य द्वारा संचालित स्रोत फीचर सेवा से जुड़े हैं। विज्ञान शिक्षण व लेखन में गहरी रुचि।