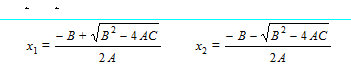विवेक मेहता [Hindi PDF, 307 kB]
 इस लेख का शीर्षक देखकर आश्चर्य में पड़ गए न कि कहाँ जेम्स बॉण्ड की दौड़ और कहाँ स्नेल्स लॉ! पर यकीन जानिए इनका आपस में सम्बन्ध है और इस लेख में हम इसी सम्बन्ध को उजागर करने की कोशिश करेंगे। तो आइए शुरुआत करते हैं...
इस लेख का शीर्षक देखकर आश्चर्य में पड़ गए न कि कहाँ जेम्स बॉण्ड की दौड़ और कहाँ स्नेल्स लॉ! पर यकीन जानिए इनका आपस में सम्बन्ध है और इस लेख में हम इसी सम्बन्ध को उजागर करने की कोशिश करेंगे। तो आइए शुरुआत करते हैं...
जेम्स बॉण्ड दौड़ पड़ा दुनिया बचाने
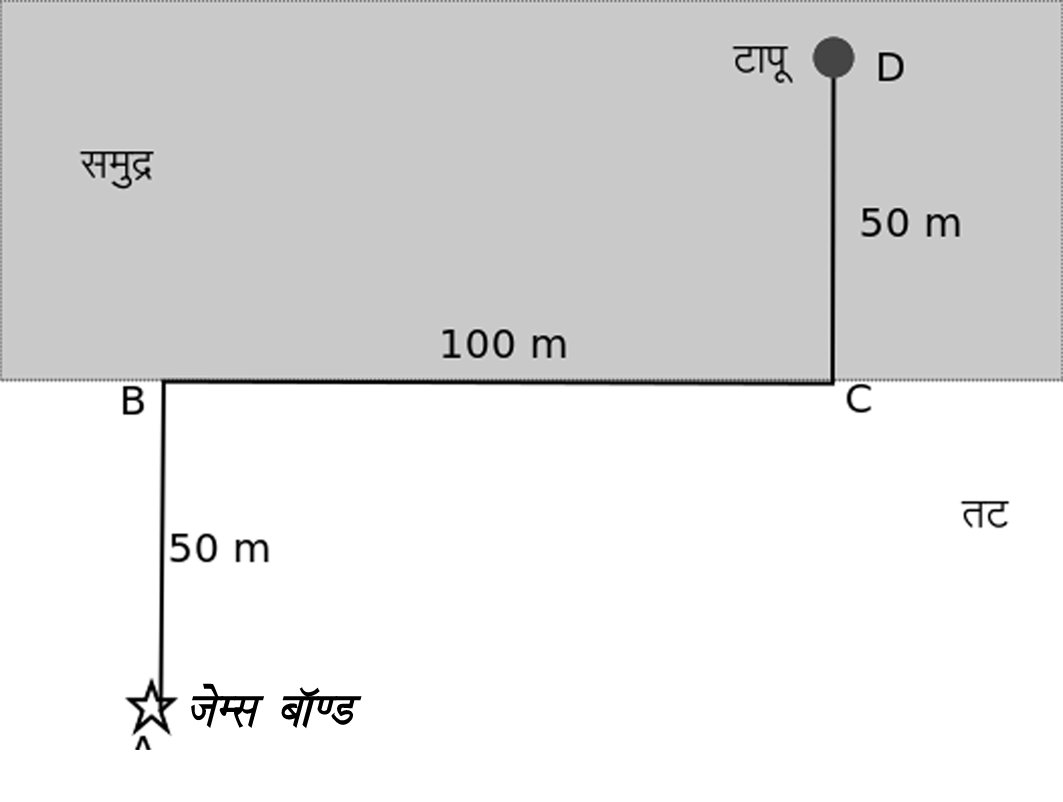
आपने शायद कभी जेम्स बॉण्ड की कोई फिल्म देखी हो। अक्सर ही उन फिल्मों में बॉण्ड खतरे में पड़ी दुनिया को बचाता हुआ पाया जाता है। चलिए एक ऐसी ही स्थिति पर विचार करते हैं जहाँ दुनिया खतरे में है और उसे बचाने का जि़म्मा जेम्स बॉण्ड के कन्धों पर आ पड़ा है क्योंकि बाकि सारे सुपर-हीरो डर कर कहीं भाग गए हैं। किसके डर से, उसके बारे में आगे। आइए देखें कि इस बार दुनिया किस खतरे में पड़ी है। दुनिया के दुश्मनों ने एक समुद्री टापू पर एक बहुत ही खतरनाक बम चालू कर के रख छोड़ा है जोकि ठीक 74 सेकण्ड बाद फटने वाला है। जेम्स बॉण्ड को उस टापू पर पहुँचकर बम को डीएक्टीवेट यानी निष्क्रिय करना है। बॉण्ड के सापेक्ष टापू की स्थिति चित्र-1 में दिखाई गई है।
बॉण्ड तट की रेतीली ज़मीन पर 5 मीटर प्रति सेकण्ड (m/s) की रफ्तार से दौड़ सकता है, समुद्र में 2 मीटर प्रति सेकण्ड की गति से तैर सकता है और एक बम को निष्क्रिय करने में उसे 30 सेकण्ड लगते हैं। ऐसी स्थिति में क्या बॉण्ड के लिए दुनिया को बचाना सम्भव होगा? अगर इस लेख को पढ़ने की पूरी कीमत वसूलना चाहते हैं तो पहले कागज़-कलम लेकर थोड़ी कोशिश कीजिए इस सवाल को हल करने की और फिर आगे बढ़िए।
अगर आपने सवाल को हल करने की दिमागी या कागज़ी या दोनों ही कोशिशें की होंगी तो आप देखेंगे कि बॉण्ड के पास कुल समय है 74 सेकण्ड जिसमें से 30 सेकण्ड तो बम को निष्क्रिय करने में ही निकल जाएँगे, तो शेष बचे 44 सेकण्ड में उसे तट से टापू पर रखे बम तक पहुँचना होगा। अगर हम तट से टापू तक पहुँचने के समय को ‘T’ से दर्शाएँ तो गणितीय तरीके से कह सकते हैं कि दुनिया को बचाने के लिए ज़रूरी है कि T< 44 s, और फिल्मी अन्दाज़ में, अगर बॉण्ड टापू तक पहुँचने में 44 सेकण्ड से ज़्यादा समय लगाएगा तो दुनिया को बचाना मुश्किल ही नहीं, नामुमकिन होगा।
टापू तक पहुँचने में लगने वाले समय की अधिकतम सीमा निकाल लेने के बाद आइए इस सवाल पर गौर करें कि बॉण्ड के पास टापू तक पहुँचने के कौन-कौन से विकल्प हैं।
विकल्प-1
पहला विकल्प जो चित्र-1 में दिखाई देता है कि बॉण्ड बिन्दु A से शुरू करके तैरते हुए सीधा टापू
यानी कि बिन्दु c तक चला जाए। अन्य सब रास्ते दूरी के मामले में इस रास्ते से लम्बेे होंगे। आइए देखें कि इस रास्ते से टापू तक पहुँचने में कितना समय लगेगा।
दो बिन्दुओं के बीच सीधी दूरी तय करने में लगने वाले समय को निकालने के लिए हमें दूरी को रफ्तार से विभाजित करना होगा। बिन्दु ॠ व क् को जोड़ने वाली सीधी रेखा समकोण त्रिभुज ॠएक् का कर्ण है, जिसकी लम्बाई हम पायथागोरस के नियम से निकाल सकते हैं। इसके मुताबिक, 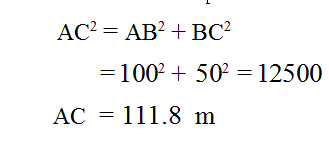

विकल्प-2
एक दूसरा विकल्प जो बॉण्ड के पास है, वो यह कि बॉण्ड पहले बिन्दु ॠ से बिन्दु ए तक दौड़ कर जाए और फिर बिन्दु ए से बिन्दु क् तक तैर कर जाए। इस सूरत में बिन्दु ॠ से बिन्दु क् तक पहुँचने में लगने वाला कुल समय होगा,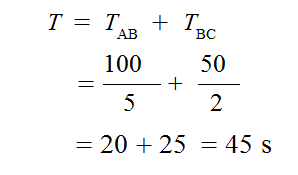
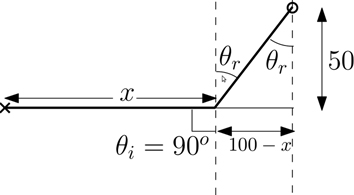
विकल्प-3 पिछले दो विकल्पों से तो बात बनी नहीं तो क्या इसका मतलब यह हुआ कि दुनिया को बचाना सम्भव नहीं? क्या कोई और तरीका है जिसका इस्तेमाल बॉण्ड कर सकता है? आइये देखते हैं। मान लीजिए कि बॉण्ड बिन्दु A से दौड़ना शुरू करे लेकिन बिन्दु B से पहले ही अपनी दौड़ खत्म करके बिन्दु C की तरफ तैरना शुरू कर दे, चित्र-2 में दिखाए अनुसार।
पिछले दो विकल्पों से तो बात बनी नहीं तो क्या इसका मतलब यह हुआ कि दुनिया को बचाना सम्भव नहीं? क्या कोई और तरीका है जिसका इस्तेमाल बॉण्ड कर सकता है? आइये देखते हैं। मान लीजिए कि बॉण्ड बिन्दु A से दौड़ना शुरू करे लेकिन बिन्दु B से पहले ही अपनी दौड़ खत्म करके बिन्दु C की तरफ तैरना शुरू कर दे, चित्र-2 में दिखाए अनुसार।
यानी बॉण्ड बिन्दु A से शुरू करके बिन्दु B’ तक x मीटर दौड़ने के बाद तैरना शुरू कर देगा। अब सवाल ये उठता है
कि x कितना हो कि बॉण्ड दुनिया को बचा पाए? पर इस सुझाव पर अमल करने से पहले आइए ये देख लें कि किसी भी न् के लिए बॉण्ड को टापू तक पहुँचने में कितना समय लगेगा। ये समय होगा,
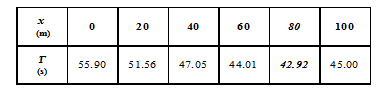
अहा! इस टेबल को देखकर हम-आप चैन की साँस ले सकते हैं क्योंकि एक स्थिति में टापू तक पहुँचने का समय 44 सेकण्ड से कम है। यानी कि अगर बॉण्ड तट पर 80 मीटर दौड़ने के बाद तैरना शुरू कर दे तो दुनिया को बचाया जा सकता है। पर यह तो हमारा तुक्का लग गया, अगर हमने 80 मीटर के लिए टापू तक पहुँचने का समय नहीं निकाला होता तो क्या हम यह कहते कि दुनिया को बचाना सम्भव नहीं? कुछ तो पक्का गणितीय तरीका होगा पूरे यकीन के साथ कह पाने का कि दुनिया को बचाना सम्भव है या नहीं। आगे की चर्चा उसी पर।
तुक्केबाज़ी नहीं पक्केबाज़ी
तीसरे विकल्प की जाँच करते हुए हमने देखा कि,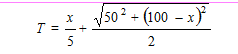
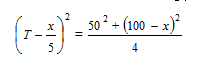

समीकरण (E-2) में T = 44 सेकण्ड रखने पर चर राशि x में मिलने वाला समीकरण होगा, इसके लिए डिस्क्रिमिनेंट (B2 – 4AC) होगा,
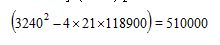
|
बॉक्स 1 द्विघाती समीकरण के हल किसी भी क्वाड्रैटिक यानी द्विघाती समीकरण को नीचे दिए गए तरीके से लिखा जा सकता है। (B2–4AC) = 0 हो तो दोनों हल वास्तविक होंगे और दोनों का ही मान —B/2A के बराबर होगा। |
अरे वाह! कहाँ अभी कुछ देर पहले तक तो हम यह सोच रहे थे कि दुनिया को बचाने का एक भी रास्ता है या नहीं, और यहाँ तो दो-दो रास्ते निकल आए और वो भी पक्के गणितीय तरीके से। अब तो बॉण्ड दुनिया को बचा ही लेगा। लेकिन एक सवाल और जो ज़हन में आता है कि क्या केवल ये दो ही तरीके हैं, या और भी विकल्प हैं जिनसे दुनिया को बचाया जा सकता है? इस सवाल पर थोड़ी देर में। उससे पहले आइए एक उदाहरण देख लें जिसमें एक दिए गए समय में दुनिया को बचाना बॉण्ड के लिए सम्भव नहीं होता।
मान लीजिए कि हमारे शुरुआती सवाल में बॉण्ड के पास कुल समय 74 सेकण्ड की जगह 72 सेकण्ड होता। ऐसी स्थिति में बॉण्ड के पास 42 सेकण्ड का समय होता टापू तक पहुँचने के लिए। आइए देखते हैं कि क्या बॉण्ड के लिए सम्भव होता इतने समय में टापू तक पहुँचना। समीकरण (E-2) में T= 42 सेकण्ड रखने पर हमें जो द्विघाती समीकरण मिलेगी वो होगी,
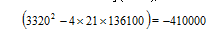
दुनिया को बचाने के कितने रास्ते?
हमने देखा कि बॉण्ड दो तरीकों से टापू तक 44 सेकण्ड में पहुँच सकता है। अब सवालों की कड़ी आगे बढ़ाएँ-
* कि क्या टापू तक 44 सेकण्ड से कम समय में पहुँचा जा सकता है? और,
* टापू तक पहुँचने में लगने वाला कम-से-कम समय कितना होगा?
इन सवालों के जवाब के लिए हम ग्राफ का सहारा लेंगे (पर यही एक तरीका है ऐसा करने का, ये बात कतई नहीं)। चित्र-3 में हमने समीकरण (E-1) यानी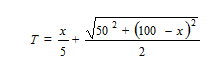
अगर इस ग्राफ में हम x-अक्ष के समानान्तर एक रेखा खींचें तो यह रेखा एक समय विशेष T को दर्शाएगी व जिन बिन्दुओं पर वह रेखा ग्राफ को काटेगी उन बिन्दुओं के लिए x का मान हमें यह बतलाएगा कि उस समय-विशेष में टापू तक पहुँचने के लिए x का मान क्या होगा। साफ तौर पर यह समीकरण हल करने का ग्राफ-आधारित तरीका हुआ। उदाहरण के तौर पर T= 44 सेकण्ड के लिए X अक्ष के समानान्तर खींची गई रेखा ग्राफ को दो बिन्दुओं पर काटती है। गौर कीजिए कि इन बिन्दुओं के लिए X के वे मान हैं जो हमने बॉक्स-1 के फॉर्मूलों से निकाले थे। वहीं दूसरी ओर T=42 सेकण्ड के लिए खींची गई रेखा ग्राफ को किसी भी बिन्दु पर नहीं काटती जिसके चलते हम न् का कोई वास्तविक मान नहीं निकाल सकते।
अब आते हैं हमारे उन दोनों सवालों पर जिनमें पहला सवाल है कि क्या टापू तक 44 सेकण्ड से कम समय में पहुँचा जा सकता है, और इसका जवाब है - हाँ। अगर बॉण्ड के द्वारा तट पर दौड़कर तय की गई दूरी 60.13 मीटर व 94.14 मीटर के बीच में हो तो टापू तक पहुँचने में लगने वाला समय 44 सेकण्ड से कम होगा। गणित की भाषा में लिखें तो, अगर 60.14 इ न् इ 94.14 तो च्र् इ 44 सेकण्ड। ग्राफ को देखकर यह जवाब आसानी से समझा जा सकता है। हम देख सकते हैं कि ग्राफ में न् उ 60.14 मीटर व न् उ 90.13 मीटर के बीच के किसी भी न् के लिए लगने वाला समय 44 सेकण्ड से कम है। अब इन दो के बीच तो बॉण्ड न् के अनगिनत मान चुन सकता है। तो इसका मतलब हुआ कि बॉण्ड के पास दुनिया को बचाने के एक नहीं, दो नहीं बल्कि अनगिनत रास्ते हैं।
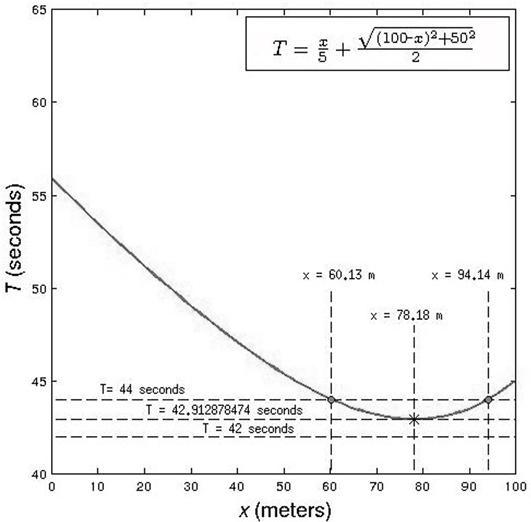 अब आते हैं दूसरे सवाल पर कि इन अनगिनत रास्तों में से वो रास्ता कौन-सा होगा जिस पर दौड़कर (व तैरकर) बॉण्ड सबसे कम समय में टापू तक पहुँच सकता है। इस सवाल का जवाब भी ग्राफ में आसानी से देखा जा सकता है। अगर आप गौर करें तो पाएँगे कि X अक्ष के समानान्तर खींची गई एक रेखा को छोड़कर बाकि सभी रेखाएँ या तो ग्राफ को दो बिन्दुओं पर काटती हैं या एक भी बिन्दु पर नहीं काटतीं। इन दोनों तरह की रेखाओं के एक-एक उदाहरण हम देख चुके हैं। अब जो एक रेखा बचती है वो बहुत खास है। T=42.91 सेकण्ड के लिए खींची गई यह रेखा खास इसलिए है क्योंकि यह ग्राफ की एक ऐसी स्पर्श-रेखा (tangent) है जिसकी ढलान (slope) शून्य है। एक दूसरी बात जो इस रेखा को इस प्रश्न से जुड़े ग्राफ के सन्दर्भ में खास बनाती है वो ये कि यह रेखा ग्राफ को दो हिस्सों में बाँटती है;
अब आते हैं दूसरे सवाल पर कि इन अनगिनत रास्तों में से वो रास्ता कौन-सा होगा जिस पर दौड़कर (व तैरकर) बॉण्ड सबसे कम समय में टापू तक पहुँच सकता है। इस सवाल का जवाब भी ग्राफ में आसानी से देखा जा सकता है। अगर आप गौर करें तो पाएँगे कि X अक्ष के समानान्तर खींची गई एक रेखा को छोड़कर बाकि सभी रेखाएँ या तो ग्राफ को दो बिन्दुओं पर काटती हैं या एक भी बिन्दु पर नहीं काटतीं। इन दोनों तरह की रेखाओं के एक-एक उदाहरण हम देख चुके हैं। अब जो एक रेखा बचती है वो बहुत खास है। T=42.91 सेकण्ड के लिए खींची गई यह रेखा खास इसलिए है क्योंकि यह ग्राफ की एक ऐसी स्पर्श-रेखा (tangent) है जिसकी ढलान (slope) शून्य है। एक दूसरी बात जो इस रेखा को इस प्रश्न से जुड़े ग्राफ के सन्दर्भ में खास बनाती है वो ये कि यह रेखा ग्राफ को दो हिस्सों में बाँटती है;
* ऊपरी हिस्सा जिसमें आने वाले किसी समय के मान के लिए हम द्विघाती समीकरण का हल निकालें तो हमें दो अलग-अलग वास्तविक हल मिलेंगे, यानी कि उसके लिए (B2 – 4AC)>0 होगा,
* निचला हिस्सा जिसमें आने वाले किसी भी समय के मान के लिए (B2 — 4AC)<0होगा यानी कि हल काल्पनिक होंगे।
अब सवाल यह उठता है कि अगर इस रेखा के ऊपर डिस्क्रिमिनेंट शून्य से बड़ा और नीचे शून्य से छोटा है तो इस रेखा पर यानी कि T= 42.912878474 सेकण्ड के लिए ये कितना होगा। समीकरण (E-2) में इतने सेकण्ड रखने पर हमें जो समीकरण मिलेगा उसके लिए डिस्क्रिमिनेंट शून्य के बराबर होगा यानी कि (B2 – 4AC)=0. अब ऐसी हालत में समीकरण के दोनों हल बराबर होंगे और उनका मान होगा x1 = x2 = 78.18 मीटर। यानी कि अगर बॉण्ड तट पर 78.18 मीटर दौड़कर तैरना शु डिग्री करे तो वह T≈ 42.91 सेकण्ड में टापू तक पहुँच जाएगा। क्या बॉण्ड इससे कम समय में टापू तक पहुँच सकता है? नहीं, क्योंकि जैसा कि हमने पहले देखा इससे कम समय के लिए समीकरण के हल काल्पनिक होंगे।
तो हमने देखा कि ग्राफ की यह स्पर्श-रेखा जिसकी ढलान शून्य है, x के उस मान को दर्शाती है जिसके लिए टापू तक पहुँचने का समय सबसे कम है। यानी कि अगर हम समीकरण (E-1) से (जो कि ग्राफ की ढलान को दर्शाता है) निकालकर, उसे शून्य के बराबर रखकर x के लिए हल करते तो हमें सीधे ही x का वो मान मिल जाता जिसके लिए टापू तक पहुँचने का समय सबसे कम होता।
वाह! ये हुई ना बात। हम अब न केवल ये बता सकते हैं कि एक दिए गए समय में बॉण्ड टापू तक पहुँचकर दुनिया को बचा सकता है या नहीं, बल्कि यह भी कि टापू तक कम-से-कम कितने समय में पहुँचा जा सकता है। और वो भी पक्के गणितीय तरीके से।
जेम्स बॉण्ड की दौड़ पर तो ढेर सारी बातें हो गईं। आइए अब कुछ बात-चीत उस नियम पर भी हो जाए जिसे हम सब स्नेल्स लॉ के नाम से जानते हैं।
स्नेल्स लॉ आप सभी ने शायद यह प्रयोग किया होगा या देखा होगा कि अगर पानी से भरी एक बाल्टी में एक लम्बी एकदम सीधी छड़ या लकड़ी डालकर देखें तो पानी की सतह से वो छड़ टेढ़ी दिखलाई देती है (चित्र-4 की तरह)। वैज्ञानिकों ने इस प्रक्रिया को प्रकाश का अपवर्तन (refraction) नाम दिया। उन्होंने पाया कि ऐसा सिर्फ पानी के साथ ही नहीं होता। जब भी प्रकाश किरणें एक माध्यम से दूसरे माध्यम में प्रवेश करती हैं तब ऐसा ही होता है। इतना जानने के बाद अब जो सवाल सामने थे, वो ये थे कि:
आप सभी ने शायद यह प्रयोग किया होगा या देखा होगा कि अगर पानी से भरी एक बाल्टी में एक लम्बी एकदम सीधी छड़ या लकड़ी डालकर देखें तो पानी की सतह से वो छड़ टेढ़ी दिखलाई देती है (चित्र-4 की तरह)। वैज्ञानिकों ने इस प्रक्रिया को प्रकाश का अपवर्तन (refraction) नाम दिया। उन्होंने पाया कि ऐसा सिर्फ पानी के साथ ही नहीं होता। जब भी प्रकाश किरणें एक माध्यम से दूसरे माध्यम में प्रवेश करती हैं तब ऐसा ही होता है। इतना जानने के बाद अब जो सवाल सामने थे, वो ये थे कि:
* प्रकाश की किरणें एक माध्यम से दूसरे माध्यम में प्रवेश करने पर क्यों मुड़ती हैं?
* प्रकाश की किरणें कितना मुड़ती हैं? और,
* उनका मुड़ना किन बातों पर निर्भर करता है?
बहुत-से वैज्ञानिक इन सवालों के जवाब ढूँढ़ने व इनसे जुड़े नियम निकालने की कोशिश कर रहे थे। पर सफलता मिली हॉलैंड के भौतिकी वैज्ञानिक विलब्रोर्ड स्नेल को जिन्होंने 1621 के आस-पास प्रकाश के अपवर्तन से जुड़े अपने प्रयोगों के दौरान यह नियम खोज निकाला1। उनके इस नियम को समझने के लिए हम चित्र-5 की मदद लेंगे।
चित्र-5 में एक प्रकाश किरण माध्यम-1 से माध्यम-2 में जा रही है। स्नेल ने अपने प्रयोगों के दौरान पाया कि जब भी ऐसा होता है तो इस पूरी प्रक्रिया में जो एक राशि नहीं बदलती वो है । यानी कि,
स्नेल ने यह भी पाया कि जब प्रकाश एक अधिक घने माध्यम से कम घने माध्यम में जाता है तो यानी कि होता है और जब प्रकाश एक कम घने माध्यम से ज़्यादा घने माध्यम में जाता है तो माने होता है।
ये नियम अपने आप में काफी बड़ी उपलब्धी थे पर अभी भी पूरी तरह से अपवर्तन की प्रक्रिया को स्पष्ट नहीं करते थे। और वैसे भी ये नियम प्रयोगों से निकाले गए थे और यह साफ नहीं था कि इस प्रक्रिया के पीछे के सिद्धान्त क्या हैं। ऐतिहासिक दस्तावेज़ों की माने तो सबसे पहले देकार्ते ने प्रकाश के अपवर्तन की सैद्धान्तिक व्याख्या दी। पर यह व्याख्या गलत थी।
प्रकाश के अपवर्तन के सिद्धान्त की सही व्याख्या दी फर्मा ने। फर्मा ने सिद्धान्त दिया कि अपवर्तन में प्रकाश की रेखाएँ इसलिए मुड़ती हैं ताकि वो अपना रास्ता कम-से-कम समय में पूरा कर सकें 2। इस सिद्धान्त के मुताबिक फर्मा ने जो फार्मूला निकाला वो था,
यहाँ V1 व V2 क्रमश: माध्यम-1 व माध्यम-2 में प्रकाश की गति हैं। ये फॉर्मूला स्नेल के प्रयोगों की खोज के साथ एकदम सही बैठता है। और आज हम तमाम किताबों में यही फॉर्मूला पढ़ते हैं।

पर मज़े की बात ये है कि हमारे बॉण्ड ने भी ये फॉर्मूला पढ़ा था और इसीलिए जब टापू तक पहुँचकर दुनिया को बचाने का सवाल उसके सामने आया तो वो डरा नहीं, अन्य सुपर-हीरो की तरह। उसने झट से ये सम्बन्ध बैठा लिया कि अपवर्तन में प्रकाश एक से दूसरे माध्यम में जाता है और दुनिया को बचाने के लिए ऐसे दो माध्यमों से गुज़रना है जिनमें उसकी गति अलग-अलग होगी।
उसने बिजली की तेज़ी से दिमाग में चित्र-6 बनाकर गणित लगाया कि
, थ्र्/द्म और थ्र्/द्म तो स्नेल के नियम के मुताबिक,


|
कुछ करने को: |
विवेक मेहता: आई.आई.टी., कानपुर से मेकेनिकल इंजीनियरिंग में पीएच.डी. की है। बीते सत्र तेजपुर विश्वविद्यालय के छात्रों को पढ़ाने की तैयारी के दौरान इस लेख की रूप-रेखा तैयार की। इन दिनों स्वतंत्र रूप से लिखने व अनुवाद का काम करते हैं।
यह लेख दो किताबों में उपलब्ध सामग्री पर आधारित है:
1. “When Least is Best” by Paul J Nahin, और
2. “Optimization: Insights and Applications” by Jan Brinkhuis and Vladimir Tikhomirov


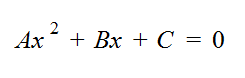 जब हम किसी समीकरण को हल करने या उसके रूट्स (हल) की बात करते हैं तो हमारा मतलब समीकरण के वेरियबल यानी कि चर राशि (इस सन्दर्भ में न्) के उन मानों को जानने से होता है जिसके लिए समीकरण का बायाँ भाग शून्य के बराबर हो।
जब हम किसी समीकरण को हल करने या उसके रूट्स (हल) की बात करते हैं तो हमारा मतलब समीकरण के वेरियबल यानी कि चर राशि (इस सन्दर्भ में न्) के उन मानों को जानने से होता है जिसके लिए समीकरण का बायाँ भाग शून्य के बराबर हो।