आमोद कारखानिस
जब शतरंज जैसे दिमागी खेल का सबसे चालाक खिलाड़ी कम्प्यूटर से हार गया तो इस बात पर बहस होने लगी कि क्या चिंतन-सृजन में भी मशीनें आदमी से बेहतर हो गई हैं? आखिर एक मशीन कैसे तय कर लेती है कि कब कौन सी चाल बेहतर होगी और किस चाल से दी जा सकती है मात?
कुछ दिनों पहले ‘डीप ब्लूच‘ कम्प्यूटर और शतरंज के विश्वविजेता गैरी कास्पारोव के बीच हुए मुकाबले में अंतिम बाज़ी कम्प्यूटर ने मार ली। शतरंज को हम सब दिगामी कौशल का खेल मानते हैं। कम्प्यूटर द्वारा शतरंज के विश्वविजेता को हराने की घटना है कि क्या इस क्षेत्र में भी कम्प्यूटर हम पर हावी हो गया है?
इसी के साथ एक और सवाल कौंधता है कि क्या कम्प्यूटर मानवीय बौद्धिक कुशाग्रता से अधिक प्रभावशाली बन गया है? और आखिर कम्प्यूटर शतरंज खेलता कैसे है? इस एक लेख में इन सब सवालों पर बात करना संभव नहीं है परन्तु इन सवालों के जवाब की दिशा में कुछ संकेत देने की कोशिश तो की ही जा सकती है।
शतरंज के खेल क एक खास बात है कि उसमें बहुत-सी चालों के बोरे में एक साथ सोचना पड़ता है। खेल में हर चाल चलते वक्त खूब सारी संभावित चालें होती हैं – जिनमें से आपको किसी एक चाल को इस आधार पर चुनना होता है कि उन सब संभावित चालों में से किस चाल को खेलने/चलने पर आपकी स्थिति आपके खिलाफ खेल रहे खिलाड़ी से बेहतर होगी। यानी आपको उन सब संभावित चालों के बारे में काफी आगे तक सोचना पड़ता है कि उनमें क्या–क्या परिस्थितियां बन सकती हैं। शतरंज के खेल या ऐसे ही किसी अन्य काम के लिए कम्प्यूटर को ज़रूरत है कृत्रिम बुद्धि(Artificial Intelligence) की। इसलिए शतरंज के बारे में बात आगे बढ़ाने से पहले ज़रा देख लें कि आखिर ‘कृत्रिम बुद्धि’ क्या बला है।
कृत्रिम बुद्धि यानी . . . .
स्कूल में जो बच्चा गणित में अच्छें अंक प्राप्त करता है उसे हम बड़ा होनहार और बुद्धिमान मानते हैं। केलकुलेटर तो गणितीय गणनाओं में मनुष्य से कई गुना तेज़ है परन्तु इसे हम कृत्रिम बुद्धि नहीं कहते। ऐसे केलकुलेटर को हम मनुष्य की आज्ञा का अत्यन्त तेज़ गति से पालन करने वाला यंत्र ही मानते हैं केवल।
खुद की गणित की परीक्षाओं को याद कीजिए। प्रश्नपत्र में कुछ सवाल आसान होते हैं, यानी ऐसे सवाल जिन्हें सुलझाने का तरीका हमें सिखाया गया है। इन सवालों को वे सब विद्यार्थी जिन्होंने सवाल सुलझाने का वह तरीका अच्छे से याद कर रखा है, सुलझा सकते हैं। परन्तु अगर कोई सवाल पेचीदा तरीके से प्रस्तुत किया गया हो तो हमारा यह रटा-रटाया तरीका नहीं चलेगा। अब कोई नया तरीका सोचना पड़ेगा – जो हमें कक्षा में सिखाई गई बातों पर आधारित हो। यहां ध्यान देने योग्य बात यह है कि इस कठिन सवाल में न केवल सवाल का हल ढूंढना है, परन्तु उस हल तक पहुंचने का रास्ता भी तलाशना होगा। यदि सवाल हल करने का तरीका ढूंढने का यह ‘तरीका’ हम कम्प्यूटर को सिखा दें तो उसे ‘कृत्रिम बुद्धि’ का दर्जा दे सकते हैं।
# क बिन्दु के निर्देशांक (4, 5) हैं और ख बिन्दु के (12, 18) क और ख के बीच की दूरी क्या है?
अगर आपको इसे हल करने का सूत्र मालूम हो तो इस प्रश्न का जवाब एकदम आसान है। यह एक पहले किस्म का सवाल है जिसमें केवल जवाब महत्वपूर्ण है।
# अब दूसरे किस्म के सवाल पर विचार करते हैं। हमारे पास दो बीकर हैं – एक का आयतन तीन लीटर है और दूसरे का चार लीटर। बीकर पर नापने के लिए और कोई निशान नहीं लगा है, और न ही हमारे पास नापने का अन्य कोई साधन है। हमें चार लीटर वाले बीकर में ठीक दो लीटर पानी चाहिए। क्या यह संभव है? कैसे?
इस प्रश्न में हल ‘क्या’ है, की बजाए ‘कैसे’ का इस्तेमाल किया गया है। यह कोई सूत्र के ज़रिए हल ढूंढने वाला सवाल नहीं है, इसमें हमें तरीका तलाशना है। थोड़ा-सा सोचकर हम इस सवाल कैसे सुलझाए जा सकते हैं यही तरीका कम्प्यूटर को भी सिखाना है। थोड़ा सोचिए इसे सुलझाने के लिए आपने किस तरह का तर्क लगाया।
साथ ही इस वाक्य पर भी ज़रा गौर करें ‘’कोई नया तरीका.... जो हमें कक्षा में सिखाई गई बातों पर आधारित हो।‘’ यानी कि समस्या का हल ढूंढने के लिए हमें ‘क्लास’ में पढ़ाई हुई बातों का ज्ञान ज़रूरी है क्यों कि हमारा नया तरीका उस ज्ञान पर आधारित है।
इसका अर्थ यह निकला कि ‘कृत्रिम बुद्धि’ से किसी समस्या को सुलझाना है तो उसकी दो प्रमुख ज़रूरतें हैं:
- ज्ञान का एक भंडार।
- जवाब तक पहुंचने का रास्ता खोज पाना।
कम्प्यूटर से सवाल-जवाब . . . .
अब तक हम गणित की बात कर रहे थे। मनुष्य की बुद्धि के दायरे में तो भाषा भी आती है। ‘कृत्रिम बुद्धि’ पर कोई भी लेख ‘एलीज़ा’ का जिक्र किए बिना पूरा नहीं हो सकता। ‘एलीज़ा’ 1966 में बनाया गया एक ऐसा कम्प्यूटर प्रोग्राम था जो एक मनोवैज्ञानिक चिकित्सक की तरह बर्ताव करता था। ‘एलीज़ा’ मानसिक मदद के लिए आए मरीजों के साथ बातचीत करती थी। यह बातचीत एक कम्प्यूटर स्क्रीन के माध्यम से होती थी। मरीज़ अपनी बात या जवाब कम्प्यूटर पर टाइप कर देता और ‘एलीज़ा’ अपने प्रश्न भी कम्प्यूटर स्क्रीन पर प्रस्तुत करती।
मरीज़ का पता होता था कि वह कम्प्यूटर से बात कर रहा है इसलिए उसे ‘एलीज़ा’ के प्रश्नों के नि:संकोच जवाब देने में कोई हिचकिचाहट नहीं होती थी।
‘एलीज़ा’ ने कृत्रिम बुद्धि और ‘मनोविज्ञान के शोध’ में अत्यन्त महत्वपूर्ण भूमिका निभाई। ‘एलीज़ा’ से वार्तालाप का एक नमूना यहां प्रस्तुत है। हालांकि ‘एलीज़ा’ के सवाल बहुत ही मानवीय थे, वे एक अत्यन्त आसान प्रोग्राम पर आधारित थे। ‘एलीज़ा’ का भाषा और मानव-शास्त्र का ज्ञान कुछ सरल नियमों पर आधारित थे। ‘एलीजा’ अपने ‘ज्ञान के भंडार’ में से ढूंढती थी कि मरीज़ के आखिरी वाक्य पर कौन-सा नियम लागू होता है और उसके मुताबिक फिर अपनी प्रतिक्रिया तैयार कर लेती थी। उदाहरण के लिए अगर मरीज़ ने टाइप किया – ‘’मेरा भाई मेरे साथ बहुत बुरी तरह से पेश आता है।‘’ तो एलीजा शायद पूछे, ‘’तुम्हारे परिवार में और कौन तुम्हारे साथ बुरी तरह से पेश आता है? नियमों की पहचान कुछ खास शब्दों से हो जाती थी इसलिए सही जवाब या प्रतिक्रिया के लिए बहुत ज़्यादा तलाश भी नहीं करनी पड़ती थी ‘एलीज़ा’ को। जब और कोई नियम न मिले तो, ‘’इसके बारे में मुझे और बताओं।‘’ ऐसे वाक्यों को दुमछल्ले की तरह चिपका दो।
एलीजा और मरीज़ की गुफ्तगू
मरीज़: सब पुरूष एक जैसे होते हैं।
एलीज़ा: किस तरह से?
मरीज़: वे सब हमें किसी न किसी चीज़ के बारे में परेशान करते रहते हैं।
एलीज़ा: क्या तुम कोई उदाहरण सोच सकती हो?
मरीज़: देखो न, मेरे पुरूष मित्र ने मुझे यहां भेज दिया।
एलीज़ा: तुम्हारे मित्र ने तुम्हें यहां क्यों भेज दिया?
मरीज़: उसका कहना है कि मैं हर समय परेशान रहती हूं।
एलीज़ा: मुझे यह सुनकर दु:ख हुआ कि तुम पेरशान रहती हो।
आपने देखा कि ये नियम एकदम अंदाज़न हैं। इन नियमों को अंदाज़न रखने के कई फायदे हैं जिनसे ऐसा आभास मिलता था कि ‘एलीजा’ वाजिब सवाल पूछ रही है। परन्तु इस सरलता की वजह से ‘एलीज़ा’ की समझ बहुत ही सतही होती और कई बार वह बहक भी जाती थी।
‘एलीज़ा’ के बाद बनाए गए मनोवैज्ञानकि कम्प्यूटरों के बारे में बात करना हमारे प्रमुख उद्देश्य शतरंज से थोड़ा हटकर होगा। इसलिए फिर लौट चलते हैं शतरंज की तरफ।
बाज़ी की शुरूआत . . .
खेल की बिसात पर सभी मोहरे सजा रखे हैं, अब खेल की शुरूआत कैसे की जाए? माना कि कम्प्यूटर सफेद मोहरों से खेल रहा है। उसकी पहली चाल क्या होगी? क्या–क्या संभावनाएं हैं? आपने बॉक्सी में दी जानकारी देखकर पाया होगा कि उसके पास कुल 20 संभावनाएं अब सवाल यह है कि वह इनमें से कौन-सी चाल चले।
इस उलझन का जवाब कई तरह से दिया जा सकता है।
- कोई भी चाल चलें खास फर्क नहीं पड़ता, अभी तो बाज़ी की शुरूआत ही हुई है। किसी भी चाल से अपना कोई भी मोहरा खतरे में नहीं पड़ सकता।
- यह तो हरेक की अपनी स्टाइल पर निर्भर करता है, मैं तो रानी वाला प्यादा आगे बढ़ाता हूं क्योंकि मुझे ‘सिसिलियन डिफेंस’ पसंद है।
- मैं सबसे पहले दाहिना घोड़ा बाहर निकालता हूं क्योंकि घोड़ा जल्द–से-जल्द आगे बढ़ाने पर बाद में बहुत काम आ सकता है।
आइए सभी जवाबों का बारी-बारी से विश्लेषण करें।
कम्प्युटर के लिए शुरुआती चालें
1. कम्प्युटर किसी भी प्यादे को एक घर आगे चल सकता है - संभावित चालें आठ
2. कम्प्युटर किसी भी प्यादे को दो घर आगे चल सकता है - संभावित चालें आठ
3. बाएं घोड़े को दो खाने में से किसी एक में रखा जा सकता है - संभावित चालें 2
4. बाएं घोड़े को दो खाने में से किसी एक में रखा जा सकता है - संभावित चालें 2
पहला जवाब प्रत्येक चाल के मूल्यांकन की तरफ इशारा करता है परन्तु उसमें सुझाया गया आकलन का पैमाना नाकाफी है। शतरंज की अगली चाल क्या होगी यह आप केवल इस आधार पर तय नहीं कर सकते कि उससे कोई मोहरा खतरे में पड़ जाएगा या सुरक्षित रहेगा। शतरंज का कोई भी अच्छा खिलाड़ी बहुत से अन्य पहलुओं पर भी गौर करेगा– क्या उस चाल से चैसबोर्ड के महत्वपूर्ण हिस्सों पर उसकी पकड़ बनेगी यानी कि उसे स्थिति लाभ मिलेगा, कहीं इस चाल की वजह से बाद में वह किसी खतरे में तो नहीं फंस जाएगा, क्या कोई तरीका है जिससे वह सामने वाले के राजा को खत्म करके मात दे सकता है... आदि।
किसी भी शतरंज खेल सकने वाले कम्प्यूटर प्रोग्राम की यह एक महत्वपूर्ण ज़रूरत होगी- संभावित चालों का मूल्यांकन कर पाने की क्षमता। और मूल्यांकन का एक सटीक तरीका।
दूसरा जवाब शतरंज के एक जाने पहचाने तरीके- ‘सिसिलियन डिफेंस’ से खेल की शुरूआत की बात करता है। शतरंज के उस्तादों ने बहुत-सी शुरूआती चालें तय करके रखी हुई हैं जिनमें कि एक हद तक सुनिश्चित होता है कि आप कौन-सा मोहरा आगे बढ़ाएंगे, सामने वाला क्या जवाब देगा, फिर आपकी चाल क्या होगी... इत्यादि।
शुरूआत की कुछ चालों के लिए तो यह तरीका काफी कारगर होता है परन्तु़ शतरंज की बिसात पर पैदा हो सकने वाली प्रत्येक स्थिति और उसका उचित जवाब कम्प्यूटर की याददाश्त (Memory) में डाल देना तकरीबन नामुमकिन है। ऐसा इसलिए क्यों कि शतरंज की बिसात पर पैदा हो सकने वाली स्थितियों की संभावनाएं बहुत ज़्यादा हैं। उन सबको सोच पाना और विश्लेषण कर पाना असंभव होगा।
मान लीजिए कि कम्प्यूटर के पास इस तरह के ज्ञान का भंडार मौजूद है फिर भी कम्प्यूटर के लिए हर बार यह खोज पाना कि बिसात की स्थिति उन लाखों करोड़ों स्थितियों में से किससे मेल खाती है, काफी मुश्किल होगा। साथ ही इस खोज में समय भी बहुत ज़्यादा लगेगा। ‘एलीला’ कम्प्यूटर प्रोग्राम की तरह अंदाजन भाषा के नियमों को पकड़ने से यहां हमारा काम नहीं चल सकता।
इसलिए याद की गई स्थितियों के आधार पर चाल चलने का तरीका कुछ शुरूआती चालों के लिए ज़रूर काम में आ सकता है परन्तु शतरंज का पूरा खेल इस तरीके से नहीं खेल जा सकता।
तीसरे जवाब में मानवीय दिमाग की एक और खासियत की तरफ इशारा किया गया है- अनुभव से सीखना।
जवाब देने वाले ने अनुभव से यह सीखा है कि शुरू से ही घोड़े को आगे रखना फायदेमंद होता है– इसलिए वह मौका मिलते ही घोड़े को अन्य मोहरों से आगे ले जाना पसंद करेगा। हमें कम्प्यूटर प्रोग्राम में चालों का मूल्यांकन करने वाले हिस्से में इस तरह की सीखने की क्षमता भी डालनी होगी।
मूल्यांकन के आधार....
शुरूआती बॉक्स में दिए गए सवाल में हम चार लीटर वाले बीकर में दो लीटर पानी डालने वाले सवाल की समस्त संभावित स्थितियों की एक सूची बना सकता हैं। उदाहरणत: इस सवाल में दस संभव स्थितियां हैं। सबसे पहले हम इनमें से कोई भी एक तरीका अपनाकर देखेंगे अगर उससे सवाल हल नहीं होता तो दूसरा तरीका अपनाएंगे और इस तरह एक के बाद एक प्रयास करते रहेंगे।
परन्तु शतरंज के खेल में एक और पेचीदगी है कि शतरंज में एक बार चाल चलने के बाद आप उसे वापस नहीं ले सकते। फिर शतरंज में हर कदम पर संभावित चालों की संख्या भी बहुत ज़्यादा होती है और एक गलत चाल चल देने से हारने की संभावना एकदम बढ़ जाती है। सही चालन की खोज सटीक मूल्यांकन से ही हो सकती है इसलिए पहले यह समझना होगा कि आखिर ‘मूल्यांकन’ किस आधार पर करें।
कम्प्यूटर द्वारा शतरंज खेलने के प्रोग्राम बनाने में ‘मूल्यांकन के सटीक व सक्षम तरीके विकसित करने’ पर काफी शोधकार्य हुए हैं। सन् 1955 के आसपास अलग-अलग मोहरों की कुल संख्या के आधार पर आकलन करने का एक आसान-सा प्रोग्राम बनाया था। इस दिशा में सन् 1960 में आर्थर सैम्युल ने पहला महत्वपूर्ण प्रयास किया। उसने अपने शतरंज प्रोग्राम में खेल के नतीजे पर असर डालने वाले बहुत से कारकों को आकलन के दायरे में रखा। मोहरों की संख्या के अलावा, आगे बढ़ पाने की क्षमता, बिसात के बीच वाले खानों पर नियंत्रय, अपनी जगह से और कही जा पाने की संभावना.... आदि जैसे पहलू चाल के मूल्यांकन की गणनाओं में शामिल किए गए थे। यह भी ख्याल रखा गया था कि प्रत्येक कारक कितना महत्वपूर्ण है, यानी कि मूल्यांकन में इसका वज़न कितना होना चाहिए। इन सब कारकों को उनके महत्व से गुणा करके जोड़ दिया जाता जिससे चाल के मूल्यांकन के लिए एक समीकरण मिल जाता।
(1 मोहरों की संख्या में फायदा) (2 आगे बढ़ पाने की क्षमता) (3 बिसात के बीच के खानों पर नियंत्रण) ....
यहां पर संख्याएं 1, 2, 3 कारकों का महत्व दर्शा रही हैं।
आकलन के लिए इस तरह का एक समीकरण होने के बावजूद विभिन्न( चालों का मूल्यांकन कर पाना इतना आसान नहीं होता। और यह तय कर पाना कि किस दिशा में बढ़ना उचित होगा और भी कठिन होता है। इस बात को हम पहाड़ की चोटी खोजने वाले उदाहरण से बखूबी समझ सकते हें।
मान लीजिए कि हमें एवरेस्ट शिखर पर चढ़ना है और अभी हम ‘बेस कैम्प’ में हैं। एवरेस्ट पर चढ़ने के लिए न तो हमारे पास कोई बना बनाया रास्ता है और न ही इस इलाके का तैयार नक्शा है। अब सवाल है कि हम अपना रास्ता कैसे खोजें।
हमें यह तो मालूम है कि एवरेस्ट सबसे ऊंचा शिखर है। अत: हमारे हर कदम का मूल्यांकन करके हम देखें कि क्या हम हर कदम में पहले की अपेक्षा ऊंचाई पर पहुंचे हैं। इसलिए हमें चारों तरफ कदम रखकर देखना होगा कि किस कदम से हम सबसे ज़्यादा ऊंचाई पाते हैं, और उस दिशा में हम आगे बढ़ जाएंगे। हर कदम पर इस तरह का आकलन करना होगा।
यह तरीका तब तक तो ठीक है अगर हम उसी पहाड़ी पर हैं जहां हमारा लक्ष्य है। अगर हम किसी उपशिखर पर पहुंच गए तो?... वहां से तो हर रास्ता नीचे ही उतरता है इसलिए वहां यह तरीका असफल रहेगा।
इस तरह की समस्या सुलझाने के भी कुछ तरीके हैं – ऐसे हालात में आप अपनी पहले वाली स्थिति पर लौटकर फिर नया रास्ता खोजने की कोशिश कर सकते हैं। पहाड़ पर चढ़ने का यह एक ‘स्थानीय’ तरीका है। इसका मतलब है कि इसमें आप केवल तुरन्त की संभावनाओं और परिणामों का आकलन करके निर्णय लेते हैं- सभी संभावनाओं के सभी परणिामों पर विचार नहीं करते।
शतरंज में अगली चाल . . . .
शतरंज में यह ज़रूरी होता है कि हम आगे की कई चालों के बारे में सोचें। यह सोचना न सिर्फ इसलिए मुश्किल होता है क्यों कि हर चरण पर संभावित चालों क संख्या बहुत ज़्यादा होती है, बल्कि इसलिए भी क्योंकि यह भी सोचना पड़ता है कि विपक्षी खिलाड़ी क्या चाल चलेगा। हालांकि कम्प्यूटर ‘खोज और मूल्यांकन’ का काम अत्यन्त तेज़ी से कर सकता है फिर भी संभावनाएं इतनी ज़्यादा हैं कि किसी भी स्तर पर संर्पूण खोजबीन नहीं की जा सकती।
इसलिए हमें ऐसा कोई तरीका ढूंढना होगा जो खोज का दायरा सीमित कर सके। आइए देखें कि अधिकतम-न्यूनतम नामक एक ऐसा तरीका कैसे काम करता है।
फायदे-नुकसान वाली चालें
संभावित चालें: एक चरण की खेज
मान लीजिए हम ‘क’ स्थिति में हैं। यहां से तीन संभव चालें हैं – ख, ग और घ। (देखिए चित्र : 1 ) इन तीनों चालों का आकलन करने पर समझ में आता है कि किसी पैमाने पर उनका मूल्य क्रमश: 8, 3 और -2 आ रहा है। इस पैमाने पर अंक जितना बड़ा हो, चाल उतनी ही बेहतर है। स्वाभाविक है कि हम ‘ख’ चाल चुनेंगे जिससे हमें सर्वाधिक फायदा हो रहा हो। यह एक ऐसा मूल्यांकन है जिसमें हम सिर्फ अपनी एक चाल तक सीमित हैं। विपक्षी का जवाब क्या होगा इस पर विचार नहीं कर रहे हैं। लेकिन हमें आगे के एक-दो चरणों में अपनी और विपक्षी की चालों पर विचार करना हो तो अन्य संभव चालों को भी मूल्यांकन के दायरे में लाना होगा। संभावित चालें : दो चरण की खोज
अब हम अगली चाल की संभावनाओं की खोज करते हैं। चित्र: 2 के अनुसार हमें अगले स्तर के मूल्यांकन पर च-छ-ज-प-फ-म-न संभावनाएं मिलती हैं। ख-ग-घ वे चालें हैं जिनमें से हमें अपनी अगली चाल चुनना है। स्वाभाविक है कि इनमें से हम वह चाल चुनेंगे जिसमें सबसे ज़्यादा फायदा हो।
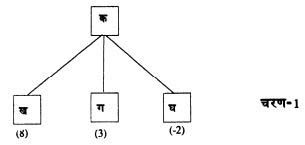
अगर हम ‘ख’ चाल चलते हैं क्योंकि चरण एक की संभावित चालों से हमें पता चला है कि वह हमारे लिए सबसे ज़्यादा फायदेमंद है – तो यकीनन हमारा विरोधी खिलाड़ी ‘छ’ चाल चलेगा क्योंकि उससे हमें सबसे कम फायदा होगा।
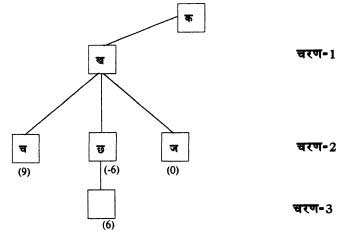
चरण दो संभावित चालों से समझ में आता है कि अगर हम ‘ख’ चाल चलें तो विरोधी ‘छ’ (-6) चलेगा, अगर हम ‘ग’ चले तो सामने वाला ‘फ’ (-2) और अगर ‘घ’ चाल चलें तो विपक्षी ‘म’ (-4) चलेगा।
इसलिए शायद हम ‘क’ स्थिति में ‘ग’ चाल चलेंगे ताकि अगली चाल में हमें नुकसान कम हो।
शायद आपका ध्यान इस ओर ज़रूर गया होगा कि हमने ‘न’ स्थिति का आकलन नहीं किया है। इसकी ज़रूरत इसलिए नहीं है क्योंकि हमें पता चल चुका है कि हमारी अभी तक की सबसे बेहतर चाल ग (3), के जवाब में विपक्षी खिलाड़ी की ‘फ’ (-2) चाल के मुकाबले ‘म’ (-4) चाल हमारे लिए काफी बुरी है। और चूंकि अगली चाल विरोधी को खेलनी है इसलिए अगर हम ‘घ’ चाल चलें तो सामने वाल म (-4) तो चलेगा ही। यह जानते हुए भला हम ‘ग’ की तुलना में ‘घ’ चाल क्यों चलें – और इसीलिए ‘न’ चाल का मूल्यांकन करने की क्या ज़रूरत है?
इसी तरह अधिकतम-न्यूनतम तरीके का इस्तेमाल करते हुए हम और गहराई में जा सकते हैं – अपने आप को संभावित चालों के दो चरणों तक सीमित रखने के बजाए कई चरणों तक खोज कर सकते हैं। समझने में आसानी हो इसलिए हमने यहां पर दोनों चरणों में बहुत कम संभावनाओं का जिक्र किया है। दरअसल शतरंज में संभावित चालें कहीं ज़्यादा होंगी और हम शायद छह – सात चरणों तक विश्लेषण करें। ऐसी स्थिति में ‘न’ का मूल्यांकन न करने से हमें न सिर्फ उस एक चाल के मूल्यांकन की बचत होती है, परन्तु उससे शुरू होने वाली बहुत-सी संभावित चालों और उनके मूल्यांकन का प्रयास भी बच जाएगा।
इस तरह की अधिकतम नयूनतम खोज हम चाहे जिस गहराई तक ले जा सकते हैं। परन्तु उतना ही ज़रूरी और हमत्वपूर्ण है यह तय कर पाना कि यह मूल्यांकन कहां पर रोक दिया जाए।
ऊपर के उदाहरण में संभव है कि ‘छ’ चाल में हमारा कोई मोहरा कुर्बान हो रहा हो – शायद ‘छ’ (-6) का मूल्य उतना ज़्यादा ऋणात्मक इसलिए है क्यों कि हमारा कोई प्रमुख मोहरा मर रहा है (देखिए चित्र-3)। अगर हम अपनी खेज यहीं रोक दें तो हम ‘ख’ चाल को इसलिए छोड़ देंगे क्योंकि अगले चरा पर वह हमारे लिए नुकसान दायक हो सकती है। संभव है कि अगली चाल में हमें भी विरोधी का उतना ही महत्वपूर्ण मोहरा मिल जाए जिससे दोनों चालों का कुल असर ‘शून्य‘ हो जाए। अगर ऐसा होता है तो चाल ‘चाल’ ‘ग’ से बेहतर है।
ऐसी अच्छी चालें छूट न जाएं इसलिए शतरंज खेलने वाले कम्प्यूटर प्रोग्राम अपनी खोज और आकलन तब तक जारी रखते हैं जब तक कि उस शाखा में बड़े-बड़े उतार-चढ़ाव खत्म न हो जाएं। यानी स्थिति शांत होती दिखाई दे तब तक मूल्यांकन और खोज जारी रखा जाता है।
शह और मात की सही चाल . . .
शतरंज के खेल में शुरूआती चालों और मात देने के लिए अंतिम चालें कैसे चली जाएं – इन दोनों पर खूब शोध हुए हैं। कौन-सी स्थिति बनने पर कौन-सी चालें चलना फायदेमंद होगा इसके विस्तृत ब्यौरे किताबों में होते हैं। कम्प्यूटर के लिए शुरूआती तयशुदा चालें चलना आसान है – परन्तु यह तय करना एक पेचीदा मसला बन जाता है कि कब कम्प्यूटर खेल के आखिरी हिस्से में किताबी –चालें चलना शुरू करे। किताबों में तो इस तरह से जानकारी दी होती है कि अगर मोहरे इन स्थितियों में हों तो आप इस तरह से चालें चलकर मात दे सकते हैं।
बिसात पर रखे हुए सब मोहरों की स्थिति किताबी जानकारी से एकदम मेल खाए यह ज़रूरी नहीं है – इसलिए ज़रूरी बन जाता है कि कम्प्यूटर बिसात पर रखे हुए मोहरों की स्थिति से वह जानकारी निकाल पाए जिसके आधार पर तय किया जा सके कि आखिरी चालें चलने का समय आ गया है या नहीं। यह एक हिस्सा है जिसमें मानव मस्तिष्क का कोई सानी नहीं।
शतरंज के खेल में शुरूआती और अंतिम चालों के लिए किताबी चालों का विस्तृत भंडार और बीच के खेल के लिए खोज और मूल्यांकन की पद्धति का इस्तेमाल आदि तरीकों को अपनाकर ही बेहतरीन कम्प्यूटर प्रोग्राम बन पाए हैं जिनकी वजह से ‘डीप ब्लू’ द्वारा शतरंज विश्व विजेता को हराना संभव हो पाया है।