पुस्तक अंश
विज्ञान के इतिहासकार जे.डी. बर्नाल की प्रसिद्ध किताब साइंस इन हिस्टरी का एक अंश
टेलिस्कोप के आविष्कार की खबर जैसे ही पाडुआ के भौतिकी और सैनिक इंजीनियरिंग के प्रोफेसर गलीलियो गलीली के कानों में पड़ी उसने खुद अपना टेलिस्कोप बनाया व उसे आकाश की ओर तान दिया। गलीलियो तब तक स्पष्ट रूप से कोपरनिकसवदी बन चुका था और पेंडुलम की गति ओर गिरती हुई वस्तुओं के अध्ययन में लगा हुआ था।
पहली कुछ रातों में उसने टेलिस्कोप से जो कुछ आकाश में देखा वह अंतरिक्ष के प्रति अरस्तूववादी धारणा को विध्वंस करने के लिए पर्याप्त था। चन्द्रमा सपाट गोला न होकर ऊंचे पहाड़ों व गहरे सागरों से ढंका था। शुक्र ग्रह में चन्द्रमा जैसी कलाएं दिख रही थीं। शनि ग्रह तीन हिस्सों में बंटा हुआ दिख रहा था। सबसे महत्वपूण्र बात उसने यह देखी कि बृहस्पति के इर्दगिर्द तीन तारे या चन्द्रमाएं परिक्रमा कर रहे थे – यानी कोपर निकस सिस्टम का एक छोटा-सा मॉडल। कोई भी इस मॉडल को टेलिस्कोप से देख सकता था।
*उत्तरी इटली का एक नगर। यहां का विश्वविद्यालय काफी प्रसिद्ध था।
**कोपरनिकस ने कहा था कि सूर्य केंद्र में है और स्थिर है। पृथ्वी व अन्य ग्रह उसके चारों ओर घूमते हैं।
***अरस्तू यह मानता था कि पृथ्वी ब्रम्हांड का स्थिर केंद्र है और सूरज, चांद और सितारे उसके इर्द-गिर्द घूमते हैं। बाद के अरस्तूवादियों के अनुसार ब्रम्हाण्ड कई स्फटिक (क्रिस्टल) गेंदों से बना हे और प्रत्येक में तारे, चांद, सूरज आदि स्थिर रूप में जड़े हुए हैं। स्फटिक गेंदों के घूमने से चांद आदि भी घूमते हुए नज़र आते हैं। इसार्इ चर्च ने इस समझ का आधार बनाकर तय किया कि पृथ्वी और उसका निवासी मानव, ईश्वरीय सृष्टि का केंद्र और चरम है। इसलिए मानव ईश्वर का विशेष कृपापात्र है।
गलीलियो गलीली (1564-1642) का चित्र। यह 1613 और 1623 में प्रकाशित उसकी किताबों में छपा था। चित्र में ऊपर के कोनों पर जो बच्चे दिखार्इ दे रहे हैं उनमें से बाएं वाला परकार पकड़े हुए है और दाएं वाले के हाथ में जो चीज़ है वे शायद गलीलियो के द्वारा बनाए गए टेलिस्कोप की पहली-पहली डिजाइन होगी।
अपनी वैज्ञानिक खोजों के विशुद्ध आनंद के साथ गलीलियो को उनका भौतिक पक्ष भी उतना ही पसंद था और उसने उनका प्रचार करने की कोशिश की। सो गलीलियो ने उन ‘नए’ तारों के नामों को उपाधियों के रूप में क्रमश: फलोरेंसे के ड्यूक, फ्रांस के राजा और पोप को बेचने की कोशिश की। पर इन लोगों को ये खगोलीय उपाधियां कुछ ज़्यादा ही महंगी लगीं। फिर गलीलियो को इनका एक ज़्यादा व्यावहारिक उपयोग सूझा कि ग्रहों के चलन के आधार पर समुद्र में देशांतर पता किए जा सकते हैं। उसने देशांतर पता करने की इस विधि को स्पेन के राजा और हॉलैंड की संसद को बेचने की कोशिश की, जिन्होंने इस खोज के लिए इनाम घोषित किए थे। लेकिन यहां भी बात नहीं बनी।
हालांकि, ये कोशिशे गलीलियो के लिए उपकथाएं थी। उसने तत्काल इन नए अवलोकनों के क्रांतिकारी महत्व को पहचाना। वह किसी को भी आकाश में कोपरनिकस के मॉडल का स्पष्ट रूप से जीता जाकता दिखा सकता था। यह जानकारी आम और खास के बीच प्रसारित करने लायक थी। एक महीने के भीतर ही 1610 में उसने एक किताब ‘सिडरियस नन्टियस’ (तारों के दूत) प्रकाशित कर दी; जो कि स्पष्ट तौर पर एक वैज्ञानिक बेस्ट सेलर थी। इसमें नए अवलोकन संक्षेप में और सफाई से प्रस्तुत किए गए थे। इस किताब ने तहलका मचा दिया लेकिन फिर भी कोई प्रतिकूल प्रतिक्रिया नहीं आर्इ। (उस पर अभियोग तो 24 साल बाद चलाया जाना था।) हालांकि 1618 में कोपरनिकस के सिद्धांतों का एक सशर्त खण्डन जारी किया गया। इससे उन सिद्धांतों को खगोलीय पिण्डों की गति का गणितीय चित्रण माने जाने में कोई बाधा नहीं आई। कुछ कट्टर अरस्तूवादियों ने टेलिस्कोप से आकाश की ओर देखने से इन्कार कर दिया क्योंकि वे मानते थे कि विशुद्ध तार्किक क्रिया से वे जानते हैं कि वहां क्या है। जब तक तर्क और अवलोकन को चर्चा के अलग-अलग दायरों में रखा जा सकता था तब तक कोई खास डर नहीं था।
चीजों का गिरना – गतिकी (Dynamics)
गलीलियो ने सोचा कि कोपरनिकस के सिद्धांतों को केवल अवलोकन के आधार पर परख लेना काफी नहीं है। उनके खिलाफ सामान्य अनुभवों और फलसफे के आधार पर पूर्व में जो अपत्तियां उठाई गईं थीं, उनका निराकरण करना ज़रूरी था और यह समझाना ज़रूरी था कि कोपरनिकस की बताई हुई व्यवस्था किस प्रकार संभव है। यह समझाना ज़रूरी था कि अगर पृथ्वी घूम रही है तो उल्टी दिशा में तेज़ हवा नहीं चलती है, और जिन चीजों कमो हम हवा में ऊपर उछालते हैं वे पीछे क्यों नहीं रह जाती हैं। इनके लिए स्वतंत्र रूप से गति करते हुए पिण्डों का अध्ययन करना ज़रूरी था। इस विषय का अध्ययन एक और व्यावहारिक कारण से महत्वपूर्ण बन चुका था- तोप से निशाने को कैसे दागें, इस की समझ बनाने के लिए।
यूनानी, अरब और फ्रांसीसियों के अध्ययन से यह धारणा प्रचलित हो रही थी कि तोप से निकलने वाले गोले में एक संवेग होता है जो कुछ समय तक उसके नीचे गिरने की प्राकृतिक प्रवृत्ति का खत्म करता है। पहले भी कई वैज्ञानिकों ने इस सिद्धांत की विवेचना की थी। उन्होंने यह बात रखी कि शुरू में गोले के तेज़ी से उठने और स्वाभाविक रूप से नीचे गिरने की क्रियाओं के बीच एक गोलाकर मिश्रित गति होती है, ये सिद्धांत उस समय तक के गोलों की गति के अवलोकनों से काफी मेल खाता था। लेकिन इसे सिद्ध करने के लिए तार्किक या गणितीय आधार उपलब्ध नहीं थे।
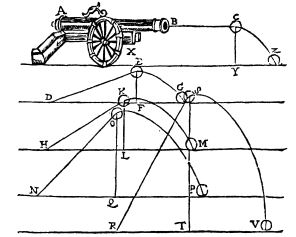तोप से दागे गए गोलों के पथ के बारे में अरस्तू ने जो कहा था वो पुनर्जागरण के काल में ही निरस्त हो पाया, जब यह पाया गया कि इन गोलों का पथ परवलयाकार (पेराबोलिक) होता है न कि दो सीधी रेखाओं के समान। लकड़ी पर उकेरा गया यह चित्र 1606 में छपी किताब में प्रकाशित हुआ था। यह हमें गलीलियो के शोध से पहले की स्थितियों के बारे में बताता है जबकि अरस्तूवाद को लेकर लोगों की असहमति साफ ज़ाहिर होने लगी थी। इस बीच के दौर में संवेग का सिद्धांत काफी प्रचलित हो चुका था जिसकी वजह से लोग मानते थे कि तोप से निकलने के बाद कुछ समय तक गोला सीधी रेखा मे रहता है।
प्रायोगिक भौतिकी
गलीलियो पिण्डों की गति का गणितीय विवरण दे पाया। यह यह उसके जीवन की सबसे महत्वपूर्ण शोधों में से था – इसका पूरा विवरण उसने अपनी किताब ‘दो नए विज्ञानों का संवाद’ में प्रकाशित किया। गलीलियों ने तब तक प्रचलित सारी मान्यताओं को चुनौती दी और वह भी एक नए तरीके की मददसे – प्रयोग के तरीके से। उसने ‘पीसा’ की झुकी मीनार से चीजें फेंक कर देखीं – यह दंत कक्षा कितनी सच है यह बहुत महत्वपूर्ण नहीं है यह बहुत महत्वपूर्ण नहीं है; हम जानते हैं कि गलीलियो ने पेंडुलम और फिसल पटद्यटी का उपयोग करके पिण्डों के गिरने का सही मापन किया।
यह आधुनिमक विज्ञान के लगभग पहले-पहले प्रयोग थे। तेरहवीं सदी के विद्वान भी प्रयोग उनसे कुछ बुनियादी मामलों में फर्क थे – पहले के विद्वान केवल सिद्धांतों को दर्शाने के लिए प्रयोग करते थे, गलीलियो ने खोज करने के लिए प्रयोग करके देखे। उसने प्रयोगो के अवलोकनों के संख्यात्मक (Quantitave) पहलू पर ध्यान दिया जिनके आधार पर प्रयोग के नतीजों को गणितीय सिद्धांतों में फिट किया जा सकता था। वैसे गलीलियो खुद अपने प्रयोगों के प्रति एक दोहरा नज़रिया दिखाता है। उसने एक बार कहा कि वह प्रयोग खुद की समझ को परखने क लिए नहीं बल्कि दूसरों को मनाने के लिए करता था। वह प्रकृति को केवल तार्किक बुद्धि के सहारे समझने की अपनी क्षमता को लेकर आश्वस्त था। इस मायने में उसके प्रयोग दर्शाने के लिए थे – खोज क लिए नहीं। लेकिन उसने उन प्रयोगों का वास्तव में करके देखा – आजकल के आदर्श ‘कागजी प्रयोग’ क विपरीत जो आधुनिक भौतिक विज्ञान का कबाड़ा किए हुए हैं; और तो और जब प्रयोग उसकी अपेक्षा क विपरीत निष्कर्ष देत तो उसने उन्हें नकारा नहीं बल्कि उल्टे अपने तर्कों व अनुमानों पर प्रश्न उठाए। तथ्य क समक्ष यह विनय-भाव प्रायोगिक विज्ञान की मुख्य विशेषता है।
गिरते हुए पिण्डों के प्रयोगों से कहीं ज़्यादा कठिन थी उनकी गणितीय विवेचना। जो बात पकड़ में आनी थी वह यह थी कि पिण्ड की गति लगातार बदलती रहती है और किसी समय बिंदु (Point of time)पर उसकी गति कुछ भी हो सकती है। दरअसल शुरू में गलीलियो का अनुमान था कि कोई पिण्ड जितना दूर चलता है उस मात्रा मे उसकी गति बढ़ती है। लेकिन उसक प्रयोगों से यह बात गलत साबित हुई और उसने खुदर स्वीकारा कि गिरता पिण्ड कितने देर से गति में है, उसकी गति इस बात पर निर्भर करती है। गिरते पिण्डों को समझने और इसके चलते हवा में गोलों की गति और आसमान मे चांद की गति, इन सबको समझने के लिए जरूरी थ यह जानना कि किसी समय बिंदु पर पिण्ड का वेग क्या होगा। यह खासी मुश्किल भौतिक अवधारणा से मेल खाती थी (Diffirential dx/dt) दो मात्राओं क बीच का अनुपात जो स्थिर बना रहता है भले ही मात्राएं खुद कितनी भी कम क्यों न हो जाएं।
गलीलियों ने इन अवधारणाओं का उपयोग ज़रूर किया लेकिन इनकी स्पष्ट विवेचना नहीं की। सटीक प्रयोग और गणितीय विश्लेषण के मिलेजुले उपयोग से उसने गिरते पिण्डों की समस्या का हल निकाला- उसने स्थापित किया कि हवा की गैर मौजूदगी में वे एक परावलयी (Parabolic) पथ बनाएंगे। यह करते हुए उसन आधुनिक भौतिकी के तरीकों की पहली स्पष्ट मिसाल पेश की जो आने वाली शताब्दियों मे बहुत ही कामयाबी के साथ विकसित होने वाले थे। वास्तव में उसने जो नपी तुली भौतिक विधि शुरू की वह हाल तक विज्ञान की बुनियादी विधि मानी गई।
पुनर्जागरण और गणित
गलीलियो और केप्लर की कामयाबी के पीछे था नए गणित पर उनका अच्छी खासी पकड़। यह गणित पुनर्जागरण के साथ विकसित हुआ था. . . विएटा नाम के गणितज्ञ ने एक निर्णयात्मक कदम उठाते हुए बीजगणित (Algebra) और त्रिकोणमिति (Trigonometry) के तर्कों में सभी ज्ञात और अज्ञात मात्राओं के लिए अक्षरों का उपयोग किया। इस परिवर्तन से गणना करने की प्रक्रिया में बहुत तेज़ी आई और शब्दों के उपयोग से जो असमंजस उत्पन्न होती थी उससे निजात मिली।
इसी तरह 1585 में सिमोन स्टेविन (1548-1620) ने दशमलव का और 1614 में नेपियर (1550-1617) ने लॉगैरिद्म (logarithms) का उपयोग शुरू किया। इनसे गणना की प्रक्रियाओं मे काफी तेज़ी आई।
अपने तर्क को पूरा करने के लिए ज़रूरी था कि गलीलियो गणित को यांत्रिकी से जोड़े। इसी प्रयास मे गलीलियो आजीवन लगा रहा। लियानार्डो विंची यांत्रिकी के मात्रात्मक पक्ष की खोज में लगा हुआ था। बेहतर प्रयोगों और गणितीय विधियों के कारण यह पक्ष गलीलियो के हाथ लगा। इस प्रकार वह वैज्ञानिक इंजीनियरिंग के प्रवर्तकों में से एक बना।
खंभे की मज़बूती के विश्लेषण के लिए गलीलियो द्वारा इस्तेमाल किया गया चित्र। इसका उपयोग उसने 1638 में छपी अपनी एक किताब में किया था।
स्थैतिकिय और गतिकी: दो नए विज्ञान
वृहत्ताकार पिण्डों की गति और चाल की समझ क लिए बलों को दो तरह से समझने की ज़रूरत है- स्थिर अवस्था या साम्यावस्था में: स्थैतिकिय और फिर इस साम्यावस्था से बाहर यानी ‘गतिकी। यही वे ‘दो नए विज्ञान’ थे जिनमें गलीलियो ने न सिर्फ गति के नियमों का आधार खोजा बल्कि पदार्थों की मज़बूती के गणितीय सिद्धांत की बुनियाद भी रखी, जिसका आधार जहाज बनाने वाले कुशल कारीगरों से हुई उसकी चर्चाएं थीं।
गलीलियो ने पहल बार स्पष्ट रूप से निरूपित किया कि पदार्थों क आवश्यक और निहित गुण वे हैं जिन्हें कि गणितीय तरीकों से मापा जा सके, ताकि उनके बारे में एक निश्चितता हो सके; और ये गुण ‘स्वाद, खुशबू, रंग आदि केवल नाम के अलावा कुछ भी नहीं हैं। वे केवल संवेदनशील पिण्डों में मौजूद हैं। नए विज्ञान क आराधकों के लिए यह एक सीमा नहीं थी। वे तो केवल सारे प्रयोगों को ‘’आकार, आकृति, मात्रा और गति’’ के बुनियादी गुणों में समेटना चाहते थे।
प्राचीन विश्व कल्पना का अंत
अपने नए गणितीय यांत्रिकी विज्ञान को मान्यता दिलवाने के लिए गलीलियो को सबसे पहले टॉलेमी के स्थिर गोलों के खगोलदर्शन का नष्ट करना था और उनके साथ अरस्तू के समूचे फलसफे का विध्वंस भी करना ज़रूरी था। अरस्तू के सिद्धांत 2000 वर्षों तक प्राकृतिक और सामाजिक विज्ञान के आधार बने रहे। गलीलियो इस काम को करने के लिए सक्षम था चूंकि ‘पाडुआ’ में उसका इस फलसफे के श्रेष्ठ स्वरूप से परिचय हुआ था। वह उस युग पुरूष को उसी के तर्क से काट सकता था ओर उसके तरीके को अन्य विद्वान अनदेखा नहीं कर सकते थे, भले ही वे उससे सहमत न हों। वैसे तो गलीलियो के सारे काम में अरस्तूवादियों का विरोध निहित था। लेकिन पहला स्पष्ट विस्फोट 1632 में हुआ जब गलीलियो ने अपनी पुस्तक ‘’ब्रम्हांड के बारे में दो प्रमुख सिद्धांतों का संवाद, टॉलमीय और कोपर्निकन’’’ को प्रकाशित किया। इस पुस्तक को उसने पोप को समर्पित किया। यह किताब विद्वानों की भाषा लेटिन में नहीं बल्कि इटालियन में थीं ताकि सभी उसे पढ़ सकें। इसमें उसने सर्वाधिक महत्व के विषयों पर अधिकृत मान्यताओं व धारणओं की धज्जियां उड़ाई। यह नए विज्ञान का पहला महान घोषणा पत्र था।
गलीलियो का मुकदमा
इस चुनौती को टाला नहीं जा सकता था और यह उसके प्रसिद्ध मुकदमे का कारण बनी। गलीलियो ने वैज्ञानिककों के बीच भी उतने ही दुश्मन बना रखे थे जितने चर्च में। इस पुस्तक के प्रकाशन के बाद दोनों उसे कुचलने के लिए जी जान से जुट गए। आज यह समझना कठिन है कि क्यों पृथ्वी और ग्रहों की गति से संबंधित यह अकादमिक मुद्दा इतने जबर्दस्त संघर्ष का कारण बना। लेकिन उन दिनों दांव पर और भी बहुत कुछ था। सदियों के संघर्ष और उच्च कोटि की दिमागी कसरत के बाद ईसाई व अरस्तू सिद्धांतों के बीच एक समझौता तैयार किया गया था। रिफॉरमेशन (धार्मिक सुधार आंदोलन) की सैद्धांतिक बहसों ने भी इस समझौते का नहीं हिलाया था।
गलीलियो की किताब ‘ब्रम्हाड के बारे में दो प्रमुख सिद्धांतों का संवाद’ का आवरण। इसमें बाई ओर अरस्तू है बीच में टॉलमी और दाहिनी ओर कोपरनिकस। इस किताब में कोपरनिकस क ‘सूर्य केंद्रित’ सिद्धांत का समर्थन किया गया था। रोमन कैथॅलिक चर्च में इस किताब को निन्दा की थी।
अगर अंतरिक्ष की संरचना जैसे एक महत्वपूर्ण पहलू को मिली चुनौती को नज़रंदाज कर दिया जाता तो यह चुनौती कितनी दूर तक वार करेगी? पहले ही उत्साही कोपर्निकस-वादियों जैसे ब्रूनो और कैम्पनेला ने इस नई विद्या से ऐसे निष्कर्ष निकाले थे जिससे चर्च, राज्य, सार्वजनिक मूल्य और यहां तक कि संपत्ति के स्थायित्व पर भी प्रश्न चिन्ह उठ गए थे।
ब्रूनो को तो जिंदा जला दिया गया था। कैम्पनेला को सालों तक कारावास में रखा था। लेकिन गलीलियो की बात कुछ और थी। उसके पास वैज्ञानिक सम्मान था और प्रभावशाली मित्र थे। उसकी धार्मिकता पर कोई शक नहीं था और विज्ञान के मामलों को छोड़कर वह क्रांतिकारी नहीं था।
मुकदमा चर्च की विचारधारा के दायरे में हुआ न कि गलीलियो के। अत: निर्णय पहले से तयशुदा था। मगर एक दिलचस्प बात यह है कि इस मुकदमे का ब्यौरा गोपनीय रखा गया। शायद इसलिए नहीं कि नयायाधीशगण गलीलियो के प्रति अपनी कठोरता को छुपाना चाहते थे- दरअसल वे उसके प्रति अपने नरम रवैये को छुपाना चाहते थे। पोप और उनके साथी चर्च के कट्टर-पंथियों की प्रतिक्रिया से ज़्यादा डरते थे, उन्हें वैज्ञानिकों की परवाह कम थी। गलीलियो का खण्डन हुआ और उसे अपने कथनों का वापस लेना पड़ा लेकिन उसे केवल नाममात्र का कारावास अपने मित्र के महल में बिताना पड़ा। फुर्सत मं वह गतिकी और स्थैतिकिय पर अपना शोध पूरा कर सका और बाद में प्रकाशित भी किया।
फिर भी यह मुकदमा एक युग की पहचान बन गया। सने धर्म और विज्ञान के बीच के संघर्ष को एक नाटकीय स्वरूप दिया। मुकदमे का निर्णय अंतत: नाकामयाब साबित हुआ क्योंकि तमाम विद्यानों ने उसे माना नहीं, और उल्टे इससे नए क्रांतिकारी प्रायोगिक विज्ञान को अप्रत्याशित सम्मान मिला। खासकर उन देशों में जहां पोप के आधिपत्य को नकारा जा चुका था। गलीलियो की कामयाबी पुराने विश्वर्दान के उन्मूलन के आखिरी और निर्णायक प्रहार बनने में थी।
उसके बाद उस दर्शन का चुपचाप नज़रंदाज़ किया जाता रहा और, खगोलविद ‘कोपरनिकन-केपलर’ के सिद्धांतों के आधार पर काम करने लगे। 40 साल बाद जाकर न्यूटन के गुरूत्वाकर्षण के सार्वभौमिक सिद्धांत में केपलर के अवलोकन आधारित नियमों को गलीलियों की गतिकी से जोड़ा जाने वाला था।
जे.डी. बर्नाल: पूरा नाम जॉन डेसमंड बर्नाल। विभिन्न विश्वविद्यालयों और कॉलेजों में पढ़ाया। 1937 में रॉयल सोसायटी के फैलो चुने गए। वे कई देशों की विज्ञान अकादमियों के सदस्य रहे। 1953में उन्हें लेनिन शांति पुरस्कार और 1959 में ग्रोटियस मेडल प्रदान किया गया।
उन्होंने र्क किताबे लिखीं हैं। ‘साइ्ंस इन हिस्ट्री‘ 1954 में पहली बार प्रकाशित हुई। इसके बाद इसके कई संसकरण निकले। यह किताब चार खण्ड में है। हाल ही में इसे ‘ऑल इंडिया पीपुल्स साइंस नेटवर्क’ ने प्रकाशित किया है।
अनुवाद: सी.एन.सुब्रम्हाण्यम; एकलव्य के सामाजिक अध्ययन शिक्षण कार्यक्रम से संबद्ध।
जुगनू की लालटेन
वेस्टइंडीज के एक क्षेत्र मे लोग इस तरह की लालटेन बनाकर इसमें जुगनू पकड़कर भर देते हैं। और अंदर चमकते-बुझते जुगनू उनका घर रोशनी से भर देते हैं। जुगनू के बारे में और अधिक जानकारी पृष्ठ 96 पर।
