प्रज्ञा कदम
एक स्कूल में गणित विषय के शिक्षक के रूप में काम करने के लिए ज़रूरत है कि शिक्षक ‘गणित और गणित-शिक्षण’ के बारे में अपने ज्ञान के बारे में सोचे और इस पर पुनर्विचार करे। स्कूलों में पढ़ाने वाले किसी भी अन्य शिक्षक की तरह मैं भी बच्चों के लिए स्कूल द्वारा तय की गई ‘गणित-पाठयपुस्तकों’ से बच्चों को गणित पढ़ाने का काम करती हूँ। ज़्यादातर समय मेरे पढ़ाने के तरीकों में ‘बताना या पाठ्यपुस्तकों में दी गई अवधारणाओं को समझाना’, ‘पूछताछ’ व ‘शंका-समाधान’ शामिल होते हैं। मैं हमेशा यह चाहती थी कि मेरे बच्चे एक विषय के रूप में गणित सीखें और उसका मज़ा लें। वे गणित से प्यार करें। यदि हम गणित को केवल बताकर या समझाकर पढ़ाने की कोशिश करेंगे तो इन उद्देश्यों को हासिल करना सम्भव नहीं है। यह बहुत ज़रूरी है कि हम तय पाठ्यपुस्तकों की सीमा से बाहर निकलें। इसलिए एक प्रोजेक्ट कार्य (जो कि एम.एड. के दौरान अनिवार्य था) के दौरान मैंने माध्यमिक शालाओं के बच्चों के साथ सीखने-सिखाने की ‘रचनात्मक-विधि’ के प्रयोग का मौका चुना। इस प्रयोग के लिए गणित का जो अध्याय चुना उसका नाम था -- आधारभूत ज्यामितीय रचनाएँ, उदाहरण के लिए किसी रेखाखण्ड के लम्बसमद्विभाजक और किसी कोण के कोण-समद्विभाजक की रचना करना।
माध्यमिक शालाओं में बच्चों को यूक्लिडियन ज्यामिति पढ़ाई जाती है। यद्यपि यूक्लिडियन ज्यामिति अमूर्त-अवधारणाओं के बारे में है, फिर भी यह हमारे आसपास की दुनिया पर लागू होती है। इसलिए शाला स्तर पर ज्यामिती पढ़ाने के दौरान हम अपने आसपास की दुनिया के अनुभवों की मदद लेते हैं।
एक गणित पढ़ाने वाली स्कूल शिक्षिका के रूप में काम करते हुए मेरी पाठ-योजना में ज़्यादातर उन गतिविधियों का समावेश होता है जो मुझे अपेक्षित सीखने के नतीजे दे सकें। मेरे पास पहले से परिभाषित व तय सीखने के नतीजे होते हैं। सीखने के ये नतीजे मेरे नियोजित व चरणबद्ध पढ़ाने के तरीकों के चलते बच्चों के व्यवहार व उनकी प्रतिक्रियाओं को तय कर रहे थे। पाठ योजना में एक विशेष तय क्रम होता था जो कि मैं इस मंशा व अपेक्षा से तैयार करती थी कि कक्षा में आने के पहले जो तय किया है, कक्षा में वही होना चाहिए।
प्रोजेक्ट का चुनाव
प्रोजेक्ट कार्य के लिए कक्षा पाँचवीं, छठवीं और सातवीं के बच्चों को चुना गया था। मैंने अपने ज़रूरी गणितीय ज्ञान को रॉबिन हार्टशोन के द्वारा लिखी किताब ज्योमेट्री: यूक्लिड एंड बियोण्ड और स्कूल की गणित की पाठ्यपुस्तकों से सीखा व समझा था। चूँकि अब तक मेरे पास रचनात्मक विधि से पढ़ाने का कोई अनुभव नहीं था और न ही मैंने ‘रचनात्मक तरीकों से सीखने-सिखाने’ के बारे में ज़्यादा पढ़ा-समझा था, इसलिए इस विधि के उपयोग व समझ के लिए मैं अपनी गाईड डॉ. सत्यवती राउल पर पूरी तरह निर्भर थी।
 विभिन्न ज्यामितीय रचनाओं के निर्माण के दौरान मैंने पाया कि सभी ज्यामितीय रचनाओं को चापों (arc) के प्रतिच्छेद (intersection) से मिलने वाले बिन्दुओं को जोड़कर बनाया जाता है। यह चाप कुछ खास नहीं हैं, बल्कि वृत्त का एक हिस्सा है। इसलिए यह कहा जा सकता है कि ज्यामितीय रचनाओं को वृत्तों के प्रतिच्छेदी बिन्दुओं को जोड़कर बनाया जाता है। अब मैंने दो वृत्तों के प्रतिच्छेद की स्थिति में ‘किसी कोण के कोण समद्विभाजक और किसी रेखाखण्ड के लम्बसमद्विभाजक’ पर ध्यान देना शुरू किया। उदाहरण के लिए, हम निम्न तरीकों में किसी रेखाखण्ड के लम्बसमद्विभाजक पर ध्यान दे सकते हैं।
विभिन्न ज्यामितीय रचनाओं के निर्माण के दौरान मैंने पाया कि सभी ज्यामितीय रचनाओं को चापों (arc) के प्रतिच्छेद (intersection) से मिलने वाले बिन्दुओं को जोड़कर बनाया जाता है। यह चाप कुछ खास नहीं हैं, बल्कि वृत्त का एक हिस्सा है। इसलिए यह कहा जा सकता है कि ज्यामितीय रचनाओं को वृत्तों के प्रतिच्छेदी बिन्दुओं को जोड़कर बनाया जाता है। अब मैंने दो वृत्तों के प्रतिच्छेद की स्थिति में ‘किसी कोण के कोण समद्विभाजक और किसी रेखाखण्ड के लम्बसमद्विभाजक’ पर ध्यान देना शुरू किया। उदाहरण के लिए, हम निम्न तरीकों में किसी रेखाखण्ड के लम्बसमद्विभाजक पर ध्यान दे सकते हैं।
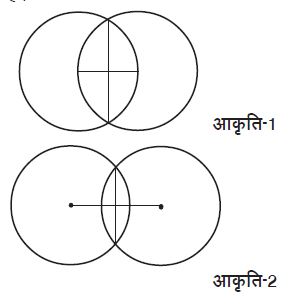
यदि दो समान वृत्त आकृति-1 के अनुसार एक-दूसरे के केन्द्रों से होकर गुज़रें तब उनके प्रतिच्छेद बिन्दुओं को आपस में जोड़ने पर हमें उन वृत्तों के केन्द्रों को मिलाने वाले रेखाखण्ड का लम्बसमद्विभाजक प्राप्त होता है।
यदि दो समान वृत्त एक-दूसरे के केन्द्रों से होकर नहीं गुज़र रहे हैं और वृत्तों के केन्द्र, प्रतिच्छेद क्षेत्र के बाहर हैं जैसा आकृति-2 में दिखाया गया है, तब भी वृत्तों के प्रतिच्छेद बिन्दुओं को आपस में जोड़ने पर हमें उन वृत्तों के केन्द्रों को मिलाने वाले रेखाखण्ड का लम्बसमद्विभाजक प्राप्त होता है।
 यदि प्रतिच्छेद करने वाले दो वृत्त समान आकार के नहीं हैं तब वृत्तों के प्रतिच्छेद बिन्दुओं को जोड़ने वाला रेखाखण्ड, वृत्तों के केन्द्रों को मिलाने वाले रेखाखण्ड पर केवल लम्ब होता है, उस रेखाखण्ड का समद्विभाजक नहीं होता है, जैसा कि आकृति-3 में दिखाया गया है।
यदि प्रतिच्छेद करने वाले दो वृत्त समान आकार के नहीं हैं तब वृत्तों के प्रतिच्छेद बिन्दुओं को जोड़ने वाला रेखाखण्ड, वृत्तों के केन्द्रों को मिलाने वाले रेखाखण्ड पर केवल लम्ब होता है, उस रेखाखण्ड का समद्विभाजक नहीं होता है, जैसा कि आकृति-3 में दिखाया गया है।
इन अवलोकनों के आधार पर मुझे लगता है कि यदि बच्चों को इन रचनाओं के अवलोकन का मौका दिया जाए तो भविष्य में वे जब किसी रेखाखण्ड के लम्बसमद्विभाजक की रचना करेंगे तो वे इन विधियों के साथ एक सम्बन्ध देख पाएँगे और यह किसी रेखाखण्ड के लम्बसमद्विभाजक की रचना करने की विधियों के बारे में सोच पाने में मदद करेगा।
रचनात्मक विधि - प्रमुख आधार
अपने गाईड के साथ सीखने-सिखाने की रचनात्मक विधि पर हुई चर्चा से मैं यह समझ पाई हूँ कि रचनावाद का आशय एक ऐसे माहौल का निर्माण करना है जो बच्चों के सीखने के लिए अनुकूल हो, जहाँ पर बच्चे विषयवस्तु या अवधारणा के बारे में अपने खुद के ज्ञान या समझ को विकसित करें। चूँकि बच्चे शिक्षक की मदद के साथ अपने खुद के ज्ञान को विकसित कर रहे हैं इसलिए इस विधि में शिक्षक की भूमिका द्वितीय यानी गौण ही रहेगी। एक शिक्षक की तरह कार्य करने की बजाय वह एक सहजकर्ता की तरह कार्य कर सकता/ती है, और सुझावों, अप्रत्यक्ष उदाहरणों और प्रश्नों के माध्यम से उनकी ज़मीनी समझ को पुख्ता करने में मदद कर सकती है। सहजकर्ता को सीधे निर्देश देने से बचना चाहिए। मैं यह भी समझ पाई कि इस विधि से शिक्षण कराने के लिए मेरे पास पहले से निर्धारित उद्देश्य नहीं होना चाहिए। इस विधि में ‘योजनाएँ’ और ‘उद्देश्य’ बच्चे की विषयवस्तु के साथ प्रगति के दौरान विकसित होते हैं। इसलिए इस प्रयोग के लिए कक्षा में इस्तेमाल की जाने वाली पूर्व-नियोजित पाठ योजना बनाना सम्भव नहीं था।
और इसी तरह प्रयोग के लिए चुने गए बच्चों के पास सीखने के इस तरीके का अभी तक कोई अनुभव नहीं था इसलिए यह ज़रूरी था कि उन्हें इस तरह से सीखने का धीरे-धीरे अनुभव दिया जाए। इस वजह से हमने सीखने को चरणबद्ध तरीके से करने की योजना बनाई। यह तय किया कि हम सीखने के पहले चरण में बच्चों के साथ ‘खुली और खोजबीन पर आधारित’ गतिविधियाँ आयोजित करेंगे जोकि अधिक चुनौती नहीं देंगी बल्कि उन्हें सीखने के नए माहौल में ढलने में मदद करेंगी।
इस प्रयोग के पहले सत्र के लिए मैंने वृत्ताकार वस्तुओं के साथ गतिविधि की योजना बनाई। यह तय किया कि हम बच्चों से ‘स्पेस या त्रिविमीय में’ और ‘सतह यानी द्विविमीय में’ वृत्ताकार वस्तुओं के बीच सम्बन्ध देखने को कहेंगे। इस सत्र के लिए हमने यह मान लिया कि बच्चे ‘स्पेस या त्रिविमीय में’, ‘सतह यानी द्विविमीय में’ और ‘सम्बन्ध’ -- इन शब्दों से भली-भाँति परिचित हैं।
सत्र की शुरुआत में मैंने वृत्ताकार चूड़ियाँ, सी.डी. और कागज़ के गोल टुकड़े बच्चों के बीच बाँट दिए। इस गतिविधि को शु डिग्री करने के लिए मैंने बच्चों को निर्देश दिया कि वे स्पेस यानी त्रिविमीय में और सतह पर यानी द्विविमीय में दो वृत्ताकार वस्तुओं के बीच में विविध सम्बन्धों को देखने की कोशिश करें। कई बच्चे ‘दो वस्तुओं के बीच सम्बन्ध’ का मतलब पूछ रहे थे। मैंने उन्हें समझाया कि इसका मतलब है कि दो वस्तुएँ एक-दूसरे से कैसे सम्बन्धित हैं। कुछ बच्चे पूछ रहे थे कि ‘स्पेस’ शब्द का क्या मतलब है। मैंने उन्हें बताया कि “वो वस्तु जिसमें केवल लम्बाई और चौड़ाई होती है उसे द्विविमीय वस्तु कहा जाता है। ये द्विविमीय वस्तुएँ एक तल पर हो सकती हैं और इसी तल को हम ‘सतह या द्विविमीय’ कहते हैं। वस्तुएँ जैसे कि कम्पास बॉक्स, बेंच, नोटबुक आदि में लम्बाई, चौड़ाई और ऊँचाई होती है। वे पूरी तरह से किसी एक तल पर नहीं आ सकती हैं इसलिए हमारे आसपास की इस जगह को हम ‘स्पेस या त्रिविमीय स्थान’ कह सकते हैं।” कक्षा पाँचवीं के बच्चे ‘लम्बाई’ और ‘चौड़ाई’ शब्दों के मतलब नहीं समझ पा रहे थे। कक्षा सातवीं के बच्चों ने ‘लम्बाई’ और ‘चौड़ाई’ शब्दों का मतलब एक कम्पास बॉक्स के उदाहरण की मदद से बताया। इस तरह से पूरा सत्र एक प्रश्न-उत्तर वाले सत्र में बदल गया था और फिर से मैं कक्षा में प्रमुख भूमिका में आ गई थी। मैं अपनी भूमिका को गौण रखने में असफल हो गई। (मुझे बच्चों को कोई सीधा निर्देश नहीं देना था, एक शिक्षक की तरह व्यवहार करने की बजाय मैं यहाँ पर एक सहजकर्ता की तरह व्यवहार नहीं कर पाई।)
जब बच्चे वृत्ताकार चीज़ों के साथ काम कर रहे थे तब ज़्यादातर बच्चों ने बराबर आकार वाली वृत्ताकार चीज़ों को चुना। इन बच्चों को पूरी तरह से आज़ादी थी कि वे इन चीज़ों के साथ जो भी अवलोकन करना चाहें, कर सकते थे। मैंने उनसे कहा कि यदि वे चाहें तो अपने अवलोकनों को कागज़ पर बना सकते हैं। बच्चों ने सबसे पहले वस्तुओं को अपने हाथ में विभिन्न स्थितियों में रखकर देखा और उन्होंने चूड़ियों को घुमा-फिराकर भी देखा। कुछ लड़कियों ने चूड़ियों को पहन भी लिया। परन्तु लम्बे समय तक बच्चों को यह समझ नहीं आया कि इस गतिविधि में आखिर करना क्या है। पूरे सत्र में वे इस बारे में सोचते रहे कि आखिर उन्हें पढ़ाया क्या जा रहा है।
इस प्रक्रिया में शिक्षक को बहुत धैर्य रखने की ज़रूरत होती है, यदि सीखने की प्रक्रिया के दौरान बच्चे मदद के लिए कहें तो सहजकर्ता को सीधे उत्तर देने की बजाय प्रति-प्रश्न पूछकर उनकी मदद करनी चाहिए। ऐसे प्रश्न पूछकर और एक ऐसे माहौल का निर्माण करने के लिए जहाँ पर बच्चे अपने ज्ञान का खुद निर्माण कर सकें, सहजकर्ता को बहुत अधिक रचनात्मक होने की ज़रूरत होती है।
हाँलाकि, रचनात्मक तरीके से सीखने-सिखाने की विधियों के लिए ज़रूरी अवधारणात्मक ज्ञान की ज़रूरत दूसरे पायदान पर है, फिर भी सहजकर्ता को अवधारणा का विस्तृत और सही ज्ञान होना ज़रूरी है। बिना सही और विस्तृत अवधारणात्मक ज्ञान के सीखने-सिखाने की यह प्रक्रिया अनुपयोगी है। यह ठीक है कि शिक्षक बच्चों के कुछ व्यवहारों के बारे में कयास लगा सकते हैं फिर भी इस बात की ज़रूरत है कि शिक्षक गतिविधि कराए जाने के दौरान उत्पन्न हो सकने वाली विभिन्न परिस्थितियों के लिए तैयार रहे।
 इस प्रयोग के दूसरे सत्र के लिए बच्चों को एक पर्चा दिया गया था जिसमें दो समान आकार के वृत्त एक-दूसरे को प्रतिच्छेद कर रहे थे। बच्चों से कहा गया था कि वे वृत्त के अन्दर, जो कुछ भी उनके अनुसार होना चाहिए, उसे बना सकते हैं।
इस प्रयोग के दूसरे सत्र के लिए बच्चों को एक पर्चा दिया गया था जिसमें दो समान आकार के वृत्त एक-दूसरे को प्रतिच्छेद कर रहे थे। बच्चों से कहा गया था कि वे वृत्त के अन्दर, जो कुछ भी उनके अनुसार होना चाहिए, उसे बना सकते हैं।
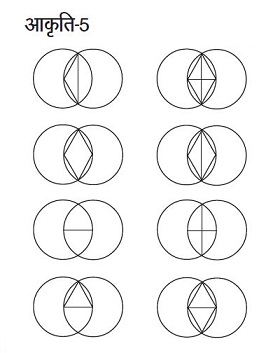 इस सत्र की योजना बनाने के दौरान हमने यह माना था कि बच्चे इन दो आकृतियों के बीचे के विशेष सम्बन्ध कि ‘यह दोनों वृत्त समान आकार के हैं और वे एक-दूसरे के केन्द्रों से होकर गुज़रेंगे’ को पहचान पाएँगे। साथ ही, हमने यह भी माना था कि बच्चे समबाहु त्रिभुज, दो समबाहु त्रिभुज, एक समचतुर्भुज, एक समद्विबाहु त्रिभुज या दो समद्विबाहु त्रिभुजों की आकृतियों को नीचे दिए गए चित्रों की तरह बनाएँगे।
इस सत्र की योजना बनाने के दौरान हमने यह माना था कि बच्चे इन दो आकृतियों के बीचे के विशेष सम्बन्ध कि ‘यह दोनों वृत्त समान आकार के हैं और वे एक-दूसरे के केन्द्रों से होकर गुज़रेंगे’ को पहचान पाएँगे। साथ ही, हमने यह भी माना था कि बच्चे समबाहु त्रिभुज, दो समबाहु त्रिभुज, एक समचतुर्भुज, एक समद्विबाहु त्रिभुज या दो समद्विबाहु त्रिभुजों की आकृतियों को नीचे दिए गए चित्रों की तरह बनाएँगे।
इस सत्र की शुरुआत में मैंने बच्चों से कहा था कि वे पर्चे में दी गई आकृति को ध्यान से देखें और वे इन वृत्तों के अन्दर किसी भी प्रकार की रचना बना सकते हैं। सभी बच्चों को पूरी तरह से आज़ादी दी गई थी। साथ ही, मैंने उन्हें यह भी कहा था कि वे अपने द्वारा बनाई गई रचनाओं को ध्यान-से देखें और अपने अवलोकनों को एक अलग कागज़ पर लिखें।
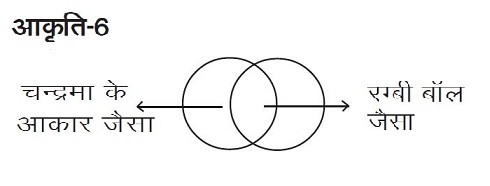 मैं यह मानकर चल रही थी कि बच्चे केवल इन रचनाओं को ही देखेंगे। और इस तरह से वे अप्रत्यक्ष रूप से एक रेखाखण्ड के लम्बसमद्विभाजक को देख पाएँगे। हाँलाकि, इस गतिविधि के दौरान कई बच्चे वृत्त के प्रतिच्छेद करने वाले हिस्से को एक ‘रग्बी बॉल के आकार जैसा’ और प्रतिच्छेद क्षेत्र के बाहर के हिस्सों को ‘चन्द्रमा के आकार जैसा’ के रूप में पहचान पाए।
मैं यह मानकर चल रही थी कि बच्चे केवल इन रचनाओं को ही देखेंगे। और इस तरह से वे अप्रत्यक्ष रूप से एक रेखाखण्ड के लम्बसमद्विभाजक को देख पाएँगे। हाँलाकि, इस गतिविधि के दौरान कई बच्चे वृत्त के प्रतिच्छेद करने वाले हिस्से को एक ‘रग्बी बॉल के आकार जैसा’ और प्रतिच्छेद क्षेत्र के बाहर के हिस्सों को ‘चन्द्रमा के आकार जैसा’ के रूप में पहचान पाए।
 कई बच्चे इस बात को देख पाए कि दो वृत्त एक-दूसरे के केन्द्र से होकर गुज़र रहे हैं। कक्षा पाँचवीं के बच्चों के लिए ‘केन्द्र’ शब्द अनजाना था। कक्षा सातवीं के एक बच्चे ने इस शब्द के अर्थ को मध्य-बिन्दु के रूप में बताया। ज़्यादातर बच्चों ने वृत्त के अन्दर अलग-अलग रचनाओं को बनाया था। ये रचनाएँ उन रचनाओं से मेल नहीं खा रही थीं जो मैंने सोच रखी थीं। मैं कक्षा में कुछ असहज महसूस कर रही थी। मैंने ‘इसके अन्दर कुछ भी बनाओ’ निर्देश देते समय यह कभी नहीं सोचा था कि बच्चे उस भाग में भी कुछ बनाएँगे जो कि दोनों वृत्तों का प्रतिच्छेद क्षेत्र है ही नहीं। इसलिए, बच्चों के लिए इस गतिविधि को चुनने के पीछे कुछ मकसद था जो कि बच्चों के द्वारा इस तरह से काम किए जाने के कारण पूरा नहीं हो पा रहा था। मुझे खीझ आने लगी थी। एक बच्चे ने दी गई आकृति में ‘समान भुजाओं वाली त्रिभुज’ को बनाया था।
कई बच्चे इस बात को देख पाए कि दो वृत्त एक-दूसरे के केन्द्र से होकर गुज़र रहे हैं। कक्षा पाँचवीं के बच्चों के लिए ‘केन्द्र’ शब्द अनजाना था। कक्षा सातवीं के एक बच्चे ने इस शब्द के अर्थ को मध्य-बिन्दु के रूप में बताया। ज़्यादातर बच्चों ने वृत्त के अन्दर अलग-अलग रचनाओं को बनाया था। ये रचनाएँ उन रचनाओं से मेल नहीं खा रही थीं जो मैंने सोच रखी थीं। मैं कक्षा में कुछ असहज महसूस कर रही थी। मैंने ‘इसके अन्दर कुछ भी बनाओ’ निर्देश देते समय यह कभी नहीं सोचा था कि बच्चे उस भाग में भी कुछ बनाएँगे जो कि दोनों वृत्तों का प्रतिच्छेद क्षेत्र है ही नहीं। इसलिए, बच्चों के लिए इस गतिविधि को चुनने के पीछे कुछ मकसद था जो कि बच्चों के द्वारा इस तरह से काम किए जाने के कारण पूरा नहीं हो पा रहा था। मुझे खीझ आने लगी थी। एक बच्चे ने दी गई आकृति में ‘समान भुजाओं वाली त्रिभुज’ को बनाया था।
 चूँकि यह रचना मेरी अपेक्षाओं के अनुसार थी इसलिए मैंने उस बच्चे की तारीफ की (मुझे उस बच्चे की तारीफ नहीं करनी चाहिए थी, क्योंकि इस विधि और गतिविधि के अनुसार हर बच्चे का चित्र सही था और हमने यह माना था कि बच्चों को अपने तरीकों को खोजना और उन पर काम करना चाहिए।) मेरी इस तारीफ ने अन्य बच्चों के व्यवहार पर प्रतिकूल प्रभाव डाला, बच्चों को लगा कि मैं उन्हें समबाहु त्रिभुज के बारे में पढ़ाना चाहती हूँ इसलिए उस बच्चे की तारीफ की है। उसके बाद तो पूरे सत्र के दौरान बच्चों ने वृत्त के अन्दर केवल समबाहु त्रिभुज के चित्र ही बनाए। अब मैं और ज़्यादा परेशान हो गई क्योंकि बच्चों ने इसके अलावा और कोई रचना नहीं बनाई जो मैं चाह रही थी।
चूँकि यह रचना मेरी अपेक्षाओं के अनुसार थी इसलिए मैंने उस बच्चे की तारीफ की (मुझे उस बच्चे की तारीफ नहीं करनी चाहिए थी, क्योंकि इस विधि और गतिविधि के अनुसार हर बच्चे का चित्र सही था और हमने यह माना था कि बच्चों को अपने तरीकों को खोजना और उन पर काम करना चाहिए।) मेरी इस तारीफ ने अन्य बच्चों के व्यवहार पर प्रतिकूल प्रभाव डाला, बच्चों को लगा कि मैं उन्हें समबाहु त्रिभुज के बारे में पढ़ाना चाहती हूँ इसलिए उस बच्चे की तारीफ की है। उसके बाद तो पूरे सत्र के दौरान बच्चों ने वृत्त के अन्दर केवल समबाहु त्रिभुज के चित्र ही बनाए। अब मैं और ज़्यादा परेशान हो गई क्योंकि बच्चों ने इसके अलावा और कोई रचना नहीं बनाई जो मैं चाह रही थी।
इसलिए मैंने तीसरे सत्र के लिए निम्न वर्क-शीट देना तय किया।
इस बार मैंने बच्चों को सख्ती से निर्देश दिया कि उन्हें केवल वृत्तों के प्रतिच्छेद वाले क्षेत्र में ही कुछ बनाना है और मुझे पक्का यकीन था कि वे केवल उन आठ रचनाओं को ही बना पाएँगे जो मैंन सोच रखी थीं। बच्चों को यह निर्देश भी दिया गया कि वे अपने अवलोकनों को उसी वर्क-शीट पर लिखें। इस बात का भी निर्देश दिया गया था कि वे बनाई गई ज्यामितीय आकृतियों को पहचानने की कोशिश करें और उन्हें ज्यामितीय नाम भी दें। इस बार मैंने कुछ प्रश्नों के साथ तैयारी की थी और मैं इन प्रश्नों का इस्तेमाल तब करती जब बच्चों से मुझे अपेक्षित रचना बनवाना हो।
| इस बार बनाई गई रचनाएँ केवल प्रतिछेच्द क्षेत्र तक सीमित थीं। कक्षा पाँच के बच्चों के द्वारा बनाई गईं रचनाओं के कुछ उदाहरण इस प्रकार थे। | कक्षा पांचवी के कुछ बच्चों ने प्रतिच्छेद क्षेत्र मे समचतुर्भुज बनाया था। जब उनसे इसके नाम के बारे मे पूछा गया तो वे इस 'पतंग' , 'हीरा' और 'काजू कतली' कह रहे थे। कक्षा छठवी के बच्चों ने निम्न रचनाओं को बनाया |
|
|
|
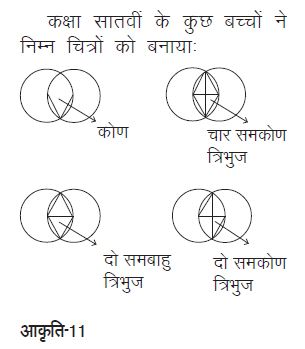
कक्षा सातवीं के कुछ बच्चों ने निम्न चित्रों को बनाया:
इस सत्र में भी बच्चों के जवाब मेरी अपेक्षाओं के अनुरूप नहीं थे। परन्तु इस बार मैंने बच्चों के जवाबों के सन्दर्भ में अपनी अपेक्षाओं से समझौता किया। कक्षा में मेरे द्वारा किए गए काम व अनुभव को लिखना इस प्रयोग का हिस्सा था, इस अनुभव लेखन व गाईड के साथ चर्चाओं ने मुझे अपने भावनात्मक सन्तुलन और आत्मविश्वास को बनाए रखने में मदद की। मैंने एक रचनात्मक सहजकर्ता की भूमिका निभाना सीखना शुरू कर दिया था
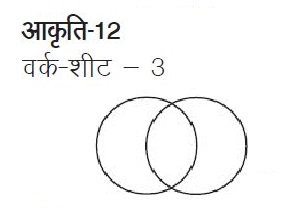 अगले सत्र के लिए बच्चों को निम्न वर्क-शीट दी गई।
अगले सत्र के लिए बच्चों को निम्न वर्क-शीट दी गई।
एक बार फिर से बच्चों को दो वृत्तों के बीच सम्बन्ध पहचानने और इस आकृति के अन्दर वे जो कुछ बनाना चाहते हैं, बनाने को कहा गया। मैंने दो वृत्तों के भीतर कोई विशेष आकृति बनाने पर ज़ोर नहीं दिया। पहले की तरह उनसे यह भी कहा गया था कि वे बनाई गई रचनाओं को नाम भी दें।
बच्चों के साथ अनौपचारिक चर्चा के लिए मैंने तैयारी की थी। (यदि रचनाएँ ज्यामितीय हुईं तब मैं बच्चों से बनाई गईं ज्यामितीय आकृति की विशेषताओं और इन विशेषताओं को ज्यामितीय उपकरणों से जाँचने के लिए कहूँगी।) यह भी तय किया गया था कि मैं बच्चों को पिछली वर्क-शीट में दिए गए सम्बन्ध के साथ इन दो वृत्तों के बीच इस विशेष सम्बन्ध की तुलना करने और इन दो अलग स्थितियों में रचना बनाने के दौरान क्या अन्तर आ रहे हैं, इसे देख पाने के लिए प्रेरित करूँगी।
 जब इस वर्क-शीट को बाँटा गया तो सभी बच्चे आसानी-से इन दो वृत्तों के बीच सम्बन्ध देख पाए। वे इसकी तुलना अपने पहले के अभ्यास से भी कर रहे थे। ज़्यादातर बच्चों ने इस तरह की आकृति बनाई।
जब इस वर्क-शीट को बाँटा गया तो सभी बच्चे आसानी-से इन दो वृत्तों के बीच सम्बन्ध देख पाए। वे इसकी तुलना अपने पहले के अभ्यास से भी कर रहे थे। ज़्यादातर बच्चों ने इस तरह की आकृति बनाई।
कक्षा सातवीं के बच्चों ने चित्र में मोटी रेखाओं से बने त्रिभुज को समद्विबाहु त्रिभुज के रूप में पहचाना। जब मैंने इसका कारण पूछा तो उन्होंने जवाब दिया कि त्रिभुज की दो भुजाएँ बराबर हैं क्योंकि वे दो समान वृत्तों की त्रिज्याएँ हैं, और तीसरी भुजा (वृत्तों के प्रतिच्छेद बिन्दुओं को जोड़ने वाला रेखाखण्ड) इन दो भुजाओं के बराबर नहीं है। बच्चों के एक अन्य समूह ने त्रिभुज की भुजाओं को नापकर देखा और यह निष्कर्ष निकाला कि यह एक समद्विबाहु त्रिभुज है। कुछ बच्चों ने व्यास ॠए और क्क़् को बनाया और यह निष्कर्ष निकाला कि चूँकि व्यास त्रिभुज के बीच में है इसलिए त्रिभुज के दोनों ओर की भुजाएँ बराबर होंगी।
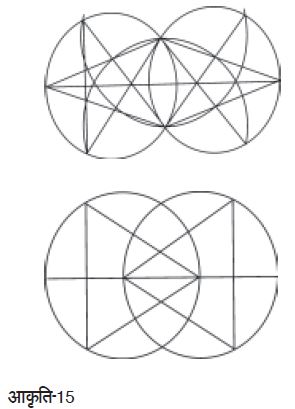
| कक्षा पाँचवीं के कुछ बच्चों ने निम्न आकृति बनाई: | कक्षा पाँचवीं के एक बच्चे ने निम्न आकृति को बनाया (आकृति-15): |
|
|
|
 वृत्तों की दो विशेष स्थितियों की तुलना करने के लिए एक बच्ची ने उसी अभ्यास पत्रक पर पूर्व की स्थिति को भी बना दिया और दो स्थितियों में वृत्तों की त्रिज्याओं में अन्तर देखने के लिए त्रिज्या को भी बना दिया। उसने इस गतिविधि को ‘वृत्तों में चित्र’ नाम भी दिया (आकृति-16)। उसने यह बताया कि हम वृत्तों के अन्दर चित्रों को बना रहे हैं, इसलिए उसने ‘वृत्तों में चित्र’ नाम रखा है।
वृत्तों की दो विशेष स्थितियों की तुलना करने के लिए एक बच्ची ने उसी अभ्यास पत्रक पर पूर्व की स्थिति को भी बना दिया और दो स्थितियों में वृत्तों की त्रिज्याओं में अन्तर देखने के लिए त्रिज्या को भी बना दिया। उसने इस गतिविधि को ‘वृत्तों में चित्र’ नाम भी दिया (आकृति-16)। उसने यह बताया कि हम वृत्तों के अन्दर चित्रों को बना रहे हैं, इसलिए उसने ‘वृत्तों में चित्र’ नाम रखा है।
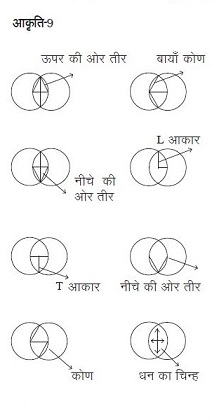
 कक्षा पाँचवीं के एक बच्चे ने बताया कि सबसे पहले एक समद्विबाहु त्रिभुज बनाया, इससे उसे अक्षर ‘ॠ’ को बनाने का विचार आया। तब उसने अन्य रेखाओं को बनाना शुरू किया और अन्य अँग्रेज़ी अक्षरों को बनाने की सम्भावनाओं को खोजना शुरू किया (आकृति-17)।
कक्षा पाँचवीं के एक बच्चे ने बताया कि सबसे पहले एक समद्विबाहु त्रिभुज बनाया, इससे उसे अक्षर ‘ॠ’ को बनाने का विचार आया। तब उसने अन्य रेखाओं को बनाना शुरू किया और अन्य अँग्रेज़ी अक्षरों को बनाने की सम्भावनाओं को खोजना शुरू किया (आकृति-17)।
सभी बच्चों ने अपनी समझ के अनुसार, उन्होंने जो भी सीखा उसकी ज़िम्मेदारी लेना शुरू किया। इस समय तक मैं भी बच्चों के प्रति अपनी अपेक्षाओं को लेकर सन्तुलन की स्थिति में आ चुकी थी। मैं यह समझ गई थी कि एक शिक्षक के रूप में जब हम बच्चों को कुछ निर्देश देते हैं तो यह ज़रूरी नहीं है कि बच्चे उसका वही मतलब समझें जो आप बताना चाहते हैं। दिए गए निर्देशों के लिए वे जो समझ विकसित करते हैं, उनकी यह समझ उनकी उम्र, परिवेश और अब तक उस परिवेश में उनके अनुभवों पर आधारित होती है। कक्षा में एक शिक्षक बच्चों को जो अनुभव देता है वे बच्चों के लिए दिए गए निर्देशों या गतिविधियों के बारे में नए अर्थ विकसित करने के मौके की तरह होते हैं। इसलिए यह ज़रूरी है कि सहजकर्ता तब तक धैर्य बनाए रखे जब तक बच्चे कक्षा में कोई गतिविधि कर रहे हैं। वह बच्चों के मौजूदा ज्ञान को समझने की कोशिश करे और इसके आधार पर नए अनुभवों और सीखने के उस वातावरण को बनाने में मदद करे जो सीखने के अपेक्षित परिणामों की ओर ले जाता है
प्रज्ञा कदम: पिछले 12 सालों से मुम्बई की विभिन्न निजी शालाओं में गणित की शिक्षिका रही हैं। स्कूली बच्चों को गणित पढ़ाने और सीखने में विशेष रुचि।
अँग्रेज़ी से अनुवाद: निदेश सोनी: एकलव्य, शाहपुर में कार्यरत हैं। गणित शिक्षण में विशेष रुचि।