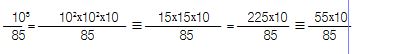लेखन : एस. श्रीनिवासन
अनुवाद: मनीषा शर्मा [Hindi PDF, 307 kB]
व्हॉट एन आइडिया सरजी!
हम जब बच्चे थे तब अपने मित्रों को लिखित गुप्त सन्देश भेजा करते थे, तब भी जब शिक्षक कक्षा में पढ़ा रहे होते थे। और राजा, दरबारी और जासूस भी यही किया करते थे। इस प्रकार के सभी प्रयासों को कूटलेखन (क्रिप्टोग्राफी) कहा जाता है - गुप्त सन्देश में लिखने का विज्ञान। ऐसी सांकेतिक कूटलिपि बनाने का मतलब आम तौर पर वर्णमाला के स्थान पर अंकों को रखने से होता था। इस प्रकार सन्देश ढेर सारे अंकों के रूप में भेजे जाते थे।
एक गुप्त संकेत लिखने के कारगर तत्व क्या हैं? यदि सन्ता कूटलिपि में लिखा कोई गुप्त सन्देश बन्ता को भेज रहा हो तो बन्ता को यह सुनिश्चित करना होगा कि सन्देश वास्तव में सन्ता के द्वारा ही भेजा गया है। साथ ही सबसे ज़रूरी है कि कोई और उस गुप्त संकेत को पढ़कर समझ न पाए, खासतौर से वह जासूस, खुफिया! और सन्ता और बन्ता के बीच उस कूटलिपि की कुंजी के आदान-प्रदान करने का एक तरीका पहले से ही तय होना चाहिए।
अंकों के रूप में भेजे गए किसी और के सन्देशों को खोल लेना, अर्थात उनकी कूटलिपि को पढ़ लेना आम तौर पर आसान होता है - जब हम कहते हैं कि आसान होता है, तो हमारा मतलब उन लोगों के लिए आसान जो ऐसी चीज़ों पर समय बर्बाद करने के लिए पर्याप्त रूप से सनकी हैं!
आइए हम एक बॉक्स के उदाहरण के ज़रिए रहस्यों का आदान-प्रदान करने के पारम्परिक तरीके को देखें। सन्ता और बन्ता दोनों के पास किसी बॉक्स की एक-एक चाबी है। सन्ता बॉक्स में अपना गुप्त सन्देश रखता है, उसमें ताला लगाता है और उसे बन्ता के पास भेज देता है। बन्ता बॉक्स को खोलने के लिए अपनी वैसी ही चाबी का इस्तेमाल करता है और सन्ता के सन्देश को पढ़ता है। यह इस पर निर्भर करता है कि सन्ता और बन्ता ने अतीत में बॉक्स की साझा चाबियाँ बनाई हों। इसे सूचना का समरूप कूटांकन (सिमिट्रिकल एनक्रिप्शन) कहा जाता है। बन्ता इसी तरीके से सन्ता को जवाब भेज सकता है। यह आपस में पहले से तय ऐसे संकेतों के रूप में सन्देश भेजने जैसा ही है, जिनकी चाबियाँ यानी सन्देश को कूटलिपि में बाँधने और उसे खोलने के आपसी रूप से तय तरीके - दोनों के पास हैं।
ऊपर दिए गए वर्णन से ऐसा मालूम होता है कि केवल वे लोग ही इस तरीके का इस्तेमाल कर सकते हैं जिनके पास पहले से किसी चाबी की एक-सी नकलें होती हैं। पर इस मजबूरी से बचने का एक रास्ता है। सन्ता अपना सन्देश बॉक्स में बन्द कर अपना ताला लगा कर बन्ता के पास भेजता है। बन्ता बॉक्स को प्राप्त करता है, अपना ताला उस पर लगाता है और उसे सन्ता के पास वापस भेज देता है। सन्ता अपने ताले को, जो उसने सबसे पहले लगाया था, खोल लेता है और बॉक्स फिर से बन्ता को भेज देता है। अब बन्ता बॉक्स को उस ताले की चाबी से खोलता है जो उसने खुद ही लगाया था। इस तरीके में सन्ता और बन्ता के बीच चाबियों का कोई आदान-प्रदान नहीं हुआ।
हालाँकि, कूटलिपि में लिखे सन्देश की स्थिति में यह जटिल हो जाता है। सन्ता अपने सन्देश को कूटलिपि में अंकित करता है, और बन्ता को भेज देता है। बन्ता उस पर आगे और कूटांकन करता है और सन्ता के पास वापस भेज देता है। सन्ता अपने कूटांकन को हटा लेता है और फिर से बन्ता के पास भेज देता है। और माना जा सकता है कि तब सन्ता के सन्देश को पढ़ने के लिए बन्ता अपना स्वयं का कूटांकन हटा लेता है। परन्तु क्या सन्ता वाकई में अपना स्वयं का कोड हटा सकता है?
मान लीजिए कि किसी सन्देश का कूटांकन करना वैसा है जैसा कि किसी गुड़िया के पैरों में मोज़े पहनाना। सन्ता के द्वारा पहनाए गए मोज़ों के ऊपर बन्ता एक जोड़ी जूते पहना देता है, और सन्ता के पास उसे वापस भेज देता है। परन्तु क्या सन्ता बन्ता द्वारा पहनाए गए जूतों को छेड़े बिना अपने द्वारा गुड़िया को पहनाए गए मोज़े निकाल सकता है? क्या आप अपनी शर्ट को हटाए बिना अपनी बनियान उतार सकते हैं? अमूमन आप ऐसा नहीं कर सकते और यह भी कि यदि वे सन्देश खुफिया के हाथों में पड़ जाते हैं तो खुफिया एक-दूसरे को भेजे गए गुप्त सन्देशों का मिलान कर सकता है और उपयुक्त जोड़ व घटाव के द्वारा सन्ता और बन्ता की गुप्त चाबियों को खोज कर सन्देश पढ़ सकता है।
सार्वजनिक कुंजी कूटलेखन
गुप्त सन्देशों को भेजने के ऊपर दिए गए सामान्य तरीकों से बेहतर एक तरीका और भी है। यह है एक सार्वजनिक कुंजी कूटलेखन का विचार फ़् और व्हॉट एन आइडिया! अब हम बिलकुल खुले तौर पर गुप्त सन्देशों को भेज सकते हैं!
गुप्त सन्देशों को भेजने के सार्वजनिक कुंजी तंत्र के ताले में तीन चाबियों के लिए तीन छेद होते हैं। चलिए हम इन्हें N E और D नाम दें। इस तंत्र में यदि ताले को N और क चाबियों के द्वारा बन्द किया जाता है, तो उसे सिर्फ N और D चाबियों द्वारा ही खोला जा सकता है। इस मामले में N और E बन्ता की सार्वजनिक चाबियाँ हैं जो सन्ता समेत हर किसी को उपलब्ध हैं जो बन्ता को गुप्त सन्देश भेजना चाहता है। पर इस सन्देश को सिर्फ बन्ता ही अपनी निजी चाबी D द्वारा खोल सकता है, अर्थात उसका कूटानुवाद कर सकता है।
और यह एक क्रान्तिकारी बात है: बन्ता की सार्वजनिक कुंजियाँ और सन्ता से प्राप्त कूटांकित सन्देश सभी लोगों, यानी खुफिया समेत किसी भी अन्य जिज्ञासु व्यक्ति के लिए उपलब्ध हैं।
कूटलेखन की सार्वजनिक कुंजी की तरकीब को, उसे खोजने वाले एम. आई. टी. गणितज्ञों - रोनाल्ड राइवेस्ट, अदि शमीर और लियोनॉर्ड एडलमैन - के नामों के शुरुआती अक्षरों के आधार पर, आर.एस.ए. विधि भी कहते हैं। हालाँकि आर.एस.ए. का मूल विचार कूटलेखन की दुनिया की एक अन्य मशहूर हस्ती विलियम डफी का था, लेकिन वे इस पर आगे अधिक काम नहीं कर सके। ब्रिटेन के गणितज्ञों ने एम.आई.टी. के गणितज्ञों से पहले ही आर.एस.ए. कूटलेखन को खोज लिया था लेकिन वे इसे सार्वजनिक नहीं कर पाए क्योंकि उनका काम सिर्फ ब्रिटिश सरकार के लिए था और इसलिए गोपनीय था!
यह कैसे काम करता है?
सबसे पहले बन्ता को बड़ी अभाज्य संख्याओं का एक युगल तय करना होता है, जैसे कि p और q । ये बन्ता की गुप्त संख्याएँ हैं। N,Pके लिए, सार्वजनिक रूप से घोषित कर देता है। लेकिन उसके pऔर q गुप्त रहते हैं, और वे किसी को भी नहीं बताए जाते।
हम छोटी संख्याओं वाला एक उदहारण लेते हैं। चलिए मान लें कि बन्ता का N = 85 है, जो 5 और 17 का गुणनफल है, यहाँ गौर करें कि ये दोनों अविभाज्य संख्याएँ हैं। इस मामले में उसका क मान लेते हैं कि 5 है (बाद में समझेंगे कि यह 5 संख्या कहां से आई)।
बन्ता को कोई सन्देश भेजने के लिए, सन्ता पहले उस सन्देश को संख्याओं में परिवर्तित करेगा। मान लीजिए सन्ता ‘बचाओ’ लिखना चाह रहा है, और कूट संख्या में मान लीजिए यह 10 बनता है। इस विधि में सन्ता को 10 को E=5 की घात तक बढ़ाना होगा, अर्थात वह 10x10x10 x10 x10 हो जाएगा। सन्ता को वास्तव में गुणनफल नहीं चाहिए, बल्कि सिर्फ उस गुणनफल को N से, जो कि 85 है, विभाजित करने पर बचा हुआ शेषफल चाहिए। गुणनफल 1,00,000 (एक लाख) है जिसे 85 से भाग देने पर शेषफल (जिसे भाग देने की लम्बी प्रक्रिया के बिना पता किया जा सकता है) 40 बचता है। इस तरह 40 वह कूट संख्या है जो सन्ता ई-मेल या फिर फोन से बन्ता को बता देता है, बिना इस बात की परवाह किए कि खुफिया या फिर कोई और उस ई-मेल को पढ़ लेगा, या फोन को बीच में ही सुन लेगा। सन्ता चाहे तो इसे अखबार में छपवा भी सकता है।
अब बन्ता यह सन्देश मिलने के बाद जिसमें 40 लिखा है अपना गुप्त नम्बर, जो कि इस मामले में D= 13 है, का इस्तेमाल करता है, और 40 की गणना 13 की घात में करता है (यह भी बाद में समझेंगे कि यह संख्या 13 कहां से आई)। यानी 40 x40 x40x40 x...13 बार। एक बार फिर बन्ता को गुणनफल की गणना करने की आवश्यकता नहीं है, उसे सिर्फ N = 85 से विभाजित करने के बाद शेषफल चाहिए। यह शेषफल 10 है। यह सीधी-सादी भाषा को संख्यात्मक रूप से बताने वाला वही अंक है, जिसका सन्ता ने कूटांकन किया है और जिसका अर्थ है ‘बचाओ’। है न अद्भुत!!
हम N, E और D तक कैसे पहुँचे?
जैसा कि ऊपर समझाया गया है, N किन्हीं बड़े अविभाज्य अंकों p और q का गुणनफल है, अर्थात N = p x q
परन्तु प्रक्रिया को समझने के लिए हम यहाँ सरल छोटे अविभाज्य अंक लेते हैं। हमारा p = 17 और q = 5 है और N = p x q = 85 है। p और q में से 1-1 घटा कर संख्याएँ निकालें और उनका गुणनफल करें, फिर उसमें 1 जोड़ें। अर्थात 16 गुणित 4 करें, फिर उसमें 1 जोड़ने पर 65 हो जाता है। अब इस 65 को दो गुणनखण्डों में बाँटें -- यही हमारे E और D हैं। इस मामले में 65 = 5 x 13 है। सिर्फ यह सावधानी रखें कि गुणक क का 64, जो कि (P-1) x (q-1) है, के गुणकों में कोई साझा गुणक नहीं हो। इस तरह हमारा E= 5 और D = 13 है।।
|
अभाज्य संख्याएँ यहाँ अभाज्य संख्याओं की कुछ विशिष्टताओं का वर्णन किया है जिनकी हमें इस लेख में आवश्यकता होगी। अभाज्य (Prime) संख्या क्या होती है? अभाज्य संख्या एक से बड़ी वह संख्या होती है जिसे एक या खुद उसी संख्या के अलावा किसी और धनात्मक संख्या से विभाजित नहीं किया जा सकता। इस तरह 13 एक अभाज्य संख्या है क्योंकि इसे सिर्फ 1 या 13 से ही विभाजित किया जा सकता है। लेकिन 20 अभाज्य संख्या नहीं है, क्योंकि यह 5 x 4 भी है। एक ऐसी संख्या जो अभाज्य नहीं है उसे संयुक्त (composite) संख्या कहा जाता है। हम 2 को अभाज्य मानते हैं, और 1 को न तो अभाज्य और न ही संयुक्त संख्या। अभाज्य गुणनखण्ड (Prime Factorisation): एक से बड़े प्रत्येक पूर्णांक को सिर्फ अभाज्य संख्याओं के उत्पाद के रूप में बाँटा जा सकता है। उदाहरण के लिए: 20 = 2x2x5, इसे 22 x 51 भी लिखा जा सकता है। और 72 = 2 x 2 x 2 x 3 x 3 जिसे 23 x32 भी लिखा जा सकता है। सहअभाज्य (Coprimes): कोई भी दो धनात्मक पूर्णांक सहअभाज्य होते हैं (या सापेक्षिक अभाज्य होते हैं) अगर उनमें 1 के अलावा कोई और साझा गुणनखण्ड न हो। अर्थात उनका जी.सी.एम. 1 होता है। इस तरह 8 और 15 सहअभाज्य हैं हालाँकि अपने आप में वे अभाज्य नहीं हैं। किसी संख्या में कितने सहअभाज्य हो सकते हैं? आइए एक अभाज्य संख्या जैसे 7 की बात करें। 7 से छोटे सभी धनात्मक पूर्णांक 7 के सहअभाज्य हैं। इस तरह 7 के 6 सहअभाज्य हैं। सामान्यत: किसी अभाज्य संख्या p के (p-1) सहअभाज्य होते हैं। उदाहरण के लिए अभाज्य 19 के 18 सहअभाज्य हैं; और अभाज्य संख्या 103 के 102 सहअभाज्य हैं। जैसा कि हमने ज़िक्र किया 1 से बड़े किसी भी पूर्णांक को अभाज्यों के उत्पाद के रूप में लिखा जा सकता है। जैसे 77 = 7 x 11 ही लीजिए, यहाँ 7 और 11 दोनों अभाज्य हैं। तब 77 में (7-1) x (11-1) सहअभाज्य होंगे यानी 77 में 60 सहअभाज्य हैं। इसे करके देखिए। |
अन्य उदाहरण
आपको यह विश्वास दिलाने के लिए कि हम चतुराई दिखाकर आपको मूर्ख बनाने की कोशिश नहीं कर रहे हैं, आइए एक और उदाहरण लें।
मान लीजिए N = p x q = 11 x 3 = 33 है। ध्यान दें कि 3 और 11 दोनों ही अभाज्य संख्याएँ हैं। अब हमारा गुणनफल (p-1) x (q-1) होगा 10 x 2 = 20, इसमें 1 जोड़ दें। हमें 21 मिलता है जो 7 x 3 का गुणफल है। यानी मेरा E है 7 और D है 3। मैं अपने N और E (यानी कि 33 और 7) सारी दुनिया को बता देता हूँ जैसे मैं अपना टेलीफोन नम्बर सबको बताता हूँ। लेकिन मैं D को गुप्त रखता हूँ और इसे किसी को भी नहीं बताता। अब मान लीजिए आप मुझे गुप्त रूप से कोई सन्देश भेजना चाहते हैं। चलिए कहें कि आप मुझे जो सन्देश भेजना चाहते हैं वह संख्या में परिवर्तित कर लिया गया है और यह अंक है 5। आप 5 पर मेरे E की घात चढ़ा देते हैं तो यह बन जाता है 57 यानी 5 x5 x 5 x 5 x 5 x 5 x 5 और इसमें अब आप N से भाग देते हैं जो कि आपके और सबके पास पहले से ही उपलब्ध है -57 = 78125 को 33 से भाग देने पर शेषफल 14 बचता है।
आप मुझे 14 कूट सन्देश के रूप में भेजते हैं। आप चाहें तो इसे सार्वजनिक रूप से भी भेज सकते हैं। जब मुझे 14 संख्या मिलती है तो मैं इस पर अपनी गुप्त संख्या 3 की घात लगा कर गणना करता हूँ, और मुझे 2744 प्राप्त होता है। इसमें 33 से भाग देने के बाद मुझे शेषफल 5 मिलता है।
यही 5 वह मूल सन्देश था जो आप मुझे भेजना चाहते थे। मुझे आपका सन्देश मिल गया! फिर से अद्भुत!!
ऊपर दिए गए दोनों उदहारणों में, शेषफल पाने के लिए आपको ‘वास्तव’ में पूरा लम्बा भाग देने की आवश्यकता नहीं है। बॉक्स देखें ‘लम्बे प्रचलित तरीके से भाग दिए बगैर शेषफल पाना।’
यह तरकीब क्यों काम करती है?
यह इसलिए काम करती है क्योंकि दो बहुत बड़ी संख्याओं का आपस में गुणा तो हर कोई कर सकता है लेकिन उस गुणा से प्राप्त संख्या के गुणनखण्ड करना इतना आसान नहीं है। यहाँ तक कि दो 200 अंकों वाली संख्याओं के गुणनफल के गुणनखण्ड निकालने में आज के सबसे बेहतरीन कंप्यूटर को उससे भी अधिक समय लग जाएगा जितनी हमारे ब्रह्माण्ड की उम्र है। इसलिए वास्तविक जीवन में होने वाले सार्वजनिक कुंजी कूटलेखन में केवल बहुत बड़ी संख्याओं का ही इस्तेमाल होता है। हकीकत तो यह है कि किसी को भी बड़ी संख्याओं का गुणनखण्ड करने की कोई आदर्श त्वरित प्रक्रिया के बारे में जानकारी नहीं है। अगर ऐसी कोई प्रक्रिया ढूँढ़ ली जाती है तो सार्वजनिक कुंजी कूटलेखन ध्वस्त हो जाएगा।
|
लम्बे प्रचलित तरीके से भाग दिए बगैर शेषफल प्राप्त करना हम ऊपर यह कहते रहे कि 10 x 10 x 10 x 10 x 10 को 85 से भाग देने के बाद प्राप्त शेषफल हासिल करने के लिए सन्ता को वास्तव में गुणनफल की आवश्यकता नहीं है। |
इसके पीछे का गणित है ऑयलर का प्रमेय (आप अगर अपने दिमाग को थोड़ी कसरत करवाना चाहते हैं तो बॉक्स देखें) जो कि फर्मेट के प्रमेय का सामान्यीकरण है। ये दोनों ही प्रमेय आधुनिक बीजगणित या अंक सिद्धान्त की किसी भी किताब के शुरुआती कुछ पन्नों में ही निपटा दिए जाते हैं।
सारांश
सन्ता सबसे पहले सन्देश को वर्णमाला के अक्षरों से संख्या में बदलता है। इस संख्या का कूटांकन करने के लिए सन्ता इस संख्या को घात E तक बढ़ाता है, और उससे प्राप्त संख्या में फिर एक दूसरी संख्या N से भाग देने के बाद शेषफल R हासिल करता है। (E तथा N, इन दोनों संख्यायों को बन्ता सार्वजनिक रूप से पहले ही घोषित कर चुका होता है।) सिर्फ यही शेषफल R बन्ता को मिलता है। इसे खोलने के लिए बन्ता शेषफल को घात D, जो सिर्फ उसे पता है, तक बढ़ाता है, और फिर N से भाग देने के बाद शेषफल प्राप्त करता है। आश्चर्य जनक रूप से बन्ता को वही संख्या मिल जाती है, जिसमें मूलत: सन्ता ने वास्तविक सन्देश को बदलकर फिर उसका कूटांकन किया था। अब बन्ता इस संख्या को फिर वर्णमाला में परिवर्तित कर सन्ता का मूल सन्देश पढ़ लेता है।
|
सन्ता और बन्ता की गणनाएँ 105 को 85 से भाग देने पर मिला शेषफल - सन्ता द्वारा शेषफल तरीके से काम करते हुए की गई गणना,
बन्ता की गणना |
खुद करके देखेंगे तो आपकी भी इस तरीके में महारत हो जाएगी।
आंकिक हस्ताक्षर
|
ऑयलर का प्रमेय हम दो अभाज्य संख्याएँ p और q लेते हैं। इनके गुणनफल p x p को ग़् के बराबर लिखते हैं। हम जानते हैं कि (बॉक्स देखें अभाज्य संख्याएँ) (p-1) x (q-1) = Φ को गुणनफल p x q के सहअभाज्यों की संख्या कह सकते हैं। इन सहअभाज्यों की संख्या में एक जोड़ दें, अर्थात Φ धन 1, यानी (Φ +1) ज्ञात कर लें। अगर आप T को खुद से (Φ + 1) बार गुणा करें, और गुणनफल को N से भाग दें, तो शेषफल भी T रहेगा। यह ऑयलर के प्रमेय का निष्कर्ष है - बल्कि उनके कई प्रमेयों में से एक का। 10 से छोटा कोई भी सम पूर्णांक लें जैसे 6। अगर 6 को (Φ +1) बार गुणा किया जाता है (यह चार धन 1 है यानी कि 5) और इसे 10 से भाग दे दें तो ऑयलर की प्रमेय कहती है कि शेषफल भी 6 ही रहेगा। अब इसे जाँच कर देखें। 6 x 6 x 6 x 6 x 6 = 7776 है जिसमें 10 से भाग देने के बाद 6 ही शेषफल रहता है। वाह! यह ऑयलर की प्रमेय का नतीजा है। अगर N एक धनात्मक पूर्णांक है, और अगर कहें कि इसमें क़ सहअभाज्य हैं। अब अगर A, N से छोटा कोई भी धनात्मक पूर्णांक है तब, आप जब A को खुद सेΦ +1 बार गुणा करके, नतीजे को N से भाग देते हैं, तो शेषफल A के अलावा कुछ और नहीं होता। कितना आश्चर्यजनक! कूटांकन के हमारे सार्वजनिक कुंजी तंत्र में वास्तव में हमने यह किया कि (Φ+1) के गुणनखण्ड D x E के रूप में कर दिए। फिर हमने कोई ऐसा धनात्मक पूर्णांक Aलिया जो Nसे छोटा है। हमने सबसे पहले AE की गणना की, फिर उसे N से विभाजित करने के बाद शेषफल की गणना की। अगर इस शेषफल को R कहें, तो एक बार फिर से RDकी गणना की। अब इसे क से विभाजित करें, तो हमें वापस अपना शेषफल A मिल जाता है। |
आपके ए.टी.एम. कार्ड के पिन नम्बर एवं आंकिक हस्ताक्षरों आदि के पीछे आर.एस.ए. सार्वजनिक कुंजी का कूटलेखन और उसके कुछ अन्य प्रकार ही होते हैं।
आइए देखें कि आंकिक हस्ताक्षर किस तरह काम करते हैं। चलिए हम अकबर और भीमराव की बात करें। इन दोनों के पास सार्वजनिक कुंजी की तरह के कूटांकन के तरीके Ea और Eb हैं, तथा इस कूटांकन को खोलने के तरीके Daऔर Db हैं। हम यह मान लेते हैं कि ऊपर दी गई विधि के समान ही, Ea और Ebऐसी सार्वजनिक कुंजी हैं जो सबको उपलब्ध हैं, जबकि Daऔर Dbनिजी कुंजी तरीके हैं जो क्रमश: सिर्फ अकबर और भीमराव को ही उपलब्ध हैं। मान लीजिए कि अकबर एक सन्देश M भीमराव को भेजना चाहता है। अकबर चाहता है कि सिर्फ भीमराव ही यह सन्देश पढ़ पाए, और साथ ही वह भीमराव को यह भरोसा भी दिलाना चाहता है कि यह सन्देश सिर्फ अकबर के पास से ही आया हो सकता है।
हम पहले इस बात पर गौर करें कि कूटांकन करने और खोलने की विधियाँ उपयोग के क्रम की दृष्टि से समरूप होती हैं - अर्थात किसी सन्देश पर Ea Da या Da Ea समान रूप से काम करते हैं, और इनका परिणाम भी समान ही होता है।
अकबर सबसे पहले अपनी खुद की कूटानुवाद खोलने की प्रक्रिया Daको सन्देश M पर उपयोग करके, फिर उस पर भीमराव की सार्वजनिक रूप से उपलब्ध कूटांकन प्रक्रिया Eb को लागू करता है, और इस प्रकार प्राप्त परिणामी सन्देश को भीमराव को भेजता है। हम इसे प्रतीकों के रूप में ऐसे कहेंगे: Eb(Da(M)) - जिसे वह भीमराव को भेज देता है। यह मिलने पर भीमराव, अपनी कूटानुवाद खोलने की प्रक्रिया Db का उपयोग करता है - इससे सन्देश का Eb हिस्सा हट जाता है, और फिर वह अकबर की सार्वजनिक रूप से उपलब्ध कूटांकन प्रक्रिया Ea कोDa(M) पर इस्तेमाल करता है - इससे सन्देश पर लागू अकबर की कूटांकन खोलने की प्रक्रिया उलट जाती है।
इसे हम ऐसे लिख सकते हैं:
(EaDa)Eb (Da(M))
=(Ea(DbEb)(Da(M)))
=(Ea (Da(M))
=M
यहाँ ध्यान दीजिए कि पहला कदम, जो किDa(M) है, सिर्फ अकबर ही उठा सकता है - इस तरह भीमराव को यह भरोसा हो जाता है कि यह सन्देश अकबर का ही भेजा हो सकता है। अब आखिरी कदम, जो अकबर से पाए गए सन्देश पर प्रक्रिया (EaDb) को लागू करना है, सिर्फ भीमराव ही उठा सकता है - जिससे अकबर को भी भरोसा रहता है कि कोई और इस सन्देश का कूटानुवाद नहीं कर सकता।
एस. श्रीनिवासन: वडोदरा में सहज और लोकॉस्ट संस्थाओं की शुरुआत व संचालन में प्रमुख भूमिका। विज्ञान एवं गणित शिक्षण में विशेष रुचि।
अँग्रेज़ी से अनुवाद: मनीषा शर्मा: शिक्षा से चिकित्सक हैं। विज्ञान और शिक्षा में गहरी दिलचस्पी। अनुवाद करने का शौक है। दिल्ली में रहती हैं।