मो. उमर
जो लोग बच्चों को पढ़ाने के काम में लगे हैं वो बखूबी समझते हैं कि भिन्न पढ़ाना कितना मुश्किल है। क्योंकि भिन्न के सवाल अक्सर बच्चों को किसी भिन्न दुनिया के लगते हैं। आप भी अपने बचपन के उस बीते समय को याद करें जब आप स्वयं भिन्न सीख रहे थे। चलिए, हम सब मिलकर बीते हुए इस कल के सफर पर चलते हैं। लेकिन उससे पहले कुछ सवाल हल करेंगे।
सवाल: नीचे दी गई भिन्न संख्याओं को बढ़ते क्रम में जमाओ।
5/6, 3/7, 1/4, 9/8, 4/5, 1/2, 1/3
सवाल: नीचे दी गई संख्याओं को बढ़ते क्रम में जमाओ।
3, 5, 2, 7, 4, 1, 9
आप शिक्षक हों या विद्यार्थी, दोनों ही सूरत में आपको पहला सवाल यानी भिन्न को बढ़ते क्रम में जमाने में ज़्यादा वक्त और एकाग्रता की ज़रूरत पड़ी होगी। ऐसी कौन-सी वजह है जो हमसे ‘भिन्न संख्या’ के हल में ज़्यादा समय की मांग कर रही है, जबकि ‘पूर्ण संख्याओं’ को एक नज़र देख कर ही हम आसानी से बढ़ते क्रम में जमा पा रहे हैं।
ऐसे कई सवालों का इस्तेमाल मैंने अपनी कार्यशालाओं में किया है और अपने अनुभवों के आधार पर कह सकता हँू कि अधिकांश लोग भिन्न को क्रम से जमाने के लिए पहले सभी भिन्न संख्याओं के हर को समान करते हैं, फिर अंश की संख्या के आधार पर बढ़ते क्रम में जमाते हैं। अन्त में वापस सवाल में दिए मूल भिन्न को बढ़ते क्रम में लिखते हैं। पूर्ण संख्या के साथ ऐसा कुछ भी करने की ज़रूरत ही नहीं पड़ती, क्योंकि संख्यांक स्वयं मात्रा का अहसास भी करा दे रहे हैं। संख्यांक 5 को देखकर पाँच वस्तुओं और संख्यांक 7 को देखकर सात वस्तुओं का भान सहज ही हो जाता है। लेकिन भिन्न संख्याओं के साथ यह इतना आसान नहीं है। इसका एक प्रमुख कारण तो यह है कि भिन्न संख्याएँ दो पूर्ण संख्याओं के नए संयोजन से बनी होती हैं। भिन्न संख्या 1/2 दो पूर्ण संख्याओं, 1 तथा 2 का नए तरह का संयोजन है जिसमें ऊपर की संख्या ‘अंश’ तथा नीचे की संख्या ‘हर’ कहलाती है। संख्या की मात्रा का अन्दाज़ा लगाने के लिए हमें पूर्ण संख्याओं के इस नए संयोजन का अर्थ समझने की ज़रूरत पड़ती है।
यह नया संयोजन कितनी मात्रा दर्शा रहा है, और क्यों? हमारी पारम्परिक कक्षाओं में यह समझ पक्की नहीं की जाती है। बल्कि समतुल्य भिन्न बनाने के मशीनी तरीके - जिसमें हम सभी भिन्न संख्याओं के हर को बराबर करते हैं - के इस्तेमाल से हम एक सरल रास्ता तो ईजाद कर लेते हैं, पर इस रास्ते पर चलकर यह नहीं जान पाते कि ऐसा क्यों कर रहे हैं? और इन भिन्नों का मात्रात्मक अहसास जान पाना... यह तो कहीं बहुत पीछे ही छूट जाता है। बल्कि यूँ कहें कि मशीनी विधि में उसकी कहीं ज़रूरत ही नहीं पड़ती।
उदाहरण के लिए ऊपर दिए गए सभी भिन्न किसी मात्रा को दर्शा रहे हैं, लेकिन हमारी विधि में मात्रा के बारे में सोचने की कोई ज़रूरत ही नहीं है। यह विधि हमें सीधे सभी भिन्नों के हर को बराबर करने को कहती है, फिर अंश की ओर ध्यान आकर्षित कर लेती है। अब हर पर ध्यान देने की ज़रूरत नहीं बचती, केवल अंश को देखिए और उन्हें बढ़ते क्रम में जमा लीजिए। बस आखिर में उन सभी मौलिक भिन्नों को दोबारा लिख लीजिए जिनके साथ आपने शुरुआत की थी। लीजिए जम गए सारे भिन्न बढ़ते क्रम में। इस पूरी प्रक्रिया में हम ‘भिन्न संख्याओं’ को अलग रख कर केवल ‘पूर्ण संख्याओं’ के साथ ही क्रिया कर रहे होते हैं -- ठीक वैसे ही जैसे हमने पूर्ण संख्याओं को बढ़ते क्रम में जमाया था।
भिन्न संख्याओं की मात्रा पर ध्यान न देने का चलन इतना व्यापक है कि कई कार्यशालाओं के दौरान मैंने पाया है कि तकरीबन 90 प्रतिशत प्रतिभागी - शिक्षक हों या छात्र - इस मशीनी तरीके का ही इस्तेमाल करके सवालों को हल करते हैं। कुछेक ने भिन्न को दशमलव में परिवर्तित करके भी बढ़ते क्रम में जमाया।
दोनों ही विधियाँ अपनाने वालों ने यदि भिन्न संख्याओं को उनके मौलिक रूप में ही देखकर मात्रा का अन्दाज़ लगाया होता तो उन्हें हर बराबर करने या दशमलव में बदलने की ज़रूरत ही नहीं पड़ती। इन लोगों ने सवाल को सही हल तो कर लिया लेकिन उनका हल यह नहीं दर्शाता कि भिन्न संख्याओं की उनकी समझ बन पाई है।
क्या भिन्न संख्याओं को उनके मौलिक रूप में ही देखकर उसकी मात्रा का अन्दाज़ लगा पाना बहुत मुश्किल है?
खामी कहाँ है?
हमारी किताबों में भिन्न से कुछ इस तरह परिचय कराया जाता है।
ऊपर 1/2, 1/4 और 3/4 के लिए बने चित्रों को दिखाकर किताबें तथा शिक्षक, दोनों ही बच्चों के मन में कुछ इस तरह की समझ विकसित करते हैं:
1/2 - एक वस्तु के दो बराबर टुकड़ों में से एक टुकड़ा ले लिया।
1/4 - एक वस्तु के चार बराबर टुकड़ों में से एक टुकड़ा ले लिया।
3/4 - एक वस्तु के चार बराबर टुकड़ों में से तीन टुकड़े ले लिए।
इसके चलते बच्चों के मन में भ्रम पनपता है कि 5/4 के लिए यह कैसे कहा जा सकता है कि एक वस्तु के चार बराबर टुकड़ों में से पाँच टुकड़े ले लिए? और 5/4 के लिए चित्र कैसे बनेगा?
ऐसी स्थिति में हम 5/4 को तोड़कर मिश्र भिन्न बनाना सिखाते हैं, फिर उसका चित्रांकन समझा पाते हैं।
5/4 = 1 और 1/4
समझ की यही गहरी खाई अक्सर ठीक-से नहीं भरी जाती है। इस भ्रम को परत-दर-परत दबाए रखते हुए भिन्न संख्याओं की जटिल संक्रियाओं की इमारत खड़ी की जाती है। इसलिए हर बार वापस पूर्ण संख्या की समझ का सहारा लेते रहना पड़ता है।
उपाय क्या है?
स्ट्रीफलैंड। ने बराबर बँटवारे (share approach) के तरीके को इस्तेमाल करते हुए भिन्न शिक्षण के क्षेत्र में व्यापक काम किया है। उनका मानना है कि भिन्न पढ़ाते समय एक मज़बूत सन्दर्भ दिया जाना चाहिए, जो बच्चों के अमूर्त चिन्तन में भी सहायक हो।
1/2 को समझाने के लिए वे कहते हैं कि यदि एक रोटी को दो लोगों में बराबर-बराबर बाँटा जाए तो हर एक को मिलने वाला हिस्सा 1/2 होगा। अंश की संख्या 1, रोटियों की संख्या दर्शाती है जिसके टुकड़ों को लोगों में बाँटना है। जबकि हर की संख्या 2, लोगों की संख्या दर्शाती है जिनमें रोटी के टुकड़ों को बराबर बाँटा जाना है।
इसी तरह 1/3 को समझाने के लिए हम एक रोटी को तीन लोगों में बराबर बाँटेंगे जिससे हर एक को मिलने वाला हिस्सा 1/3 प्राप्त किया जा सकता है।
इस तरह 1/2 (एक रोटी को दो लोगों में बराबर-बराबर बाँटा) और 1/3 (एक रोटी को तीन लोगों में बराबर-बराबर बाँटा) को देखकर ही हम जान सकते हैं कि कौन-सा भिन्न बड़ा है और कौन-सा छोटा है। इसी तरीके को अपनाकर 1/2, 1/4, 3/4 और 5/4 की मात्रा का अहसास आसानी से विकसित किया जा सकता है।
अब हम वापस अपने सवाल पर चलते हैं। बराबर बँटवारे के इसी तरीके को अपनाकर हम नीचे लिखी भिन्न संख्याओं को बढ़ते क्रम में जमाने की कोशिश करेंगे।
5/6, 3/7, 1/4, 9/8, 4/5, 1/2, 1/3
सभी भिन्न संख्याओं में से 1/2 को अपनी आधार संख्या मान लेते हैं। एक रोटी को दो लोगों में बराबर बाँटो, तीन लोगों में बराबर बाँटो और यदि चार लोगों में बराबर बाँटो तो किस मात्रा में टुकड़े मिलेंगे, इसका अन्दाज़ लगाया जा सकता है।
यह तरीका मन ही मन सोचने भर से ही हमें एक मोटा अनुमान देगा कि...
1/4 से बड़ा 1/3 से बड़ा 1/2
अत: 1/4 इ 1/3 इ 1/2
अब हम 3/7 को देखेंगे। यदि 3 रोटी को 6 लोगों में बराबर-बराबर बाँटा जाए तो प्रत्येक व्यक्ति को आधी-आधी यानी 1/2 हिस्सा मिलता, लेकिन चूँकि लोगों की संख्या सात है तो सबको 1/2 हिस्से से कम ही मिल पाएगा।
इसी तरह 4/5 और 5/6 में आधी से ज़्यादा मिल पाएगी। 9/8 को तो देखकर ही हम जान सकते हैं कि रोटी 9 हैं और लोग 8, तो हर एक व्यक्ति को एक से ज़्यादा रोटी मिलेगी।
इस अन्दाज़े को क्रम में जमाते हैं।
(3/7) (4/5, 5/6)
1/4 < 1/3 < 1/2 < 9/8
3/7 के बारे में यह तो पक्के तौर से कहा जा सकता है कि यह 1/2 से कम है। लेकिन क्या यह 1/3 से भी कम है या फिर ज़्यादा है?
1/3 के मायने हैं 1 रोटी को 3 लोगों में बराबर-बराबर बाँटा जो कि 3 रोटी को 9 लोगों में बराबर-बराबर बाँटने के समतुल्य है। लेकिन यहाँ पर 3/7 में 3 रोटी को 7 लोगों में ही बराबर-बराबर बाँटा जा रहा है। इसका मतलब है कि यह 1/3 से बड़ा भिन्न होगा। इसे जमा लेते हैं।
(4/5, 5/6)
1/4 < 1/3 < 3/7 < 1/2 < 9/8
अब भी 4/5 और 5/6 के बीच कौन बड़ा है, कौन छोटा है, इसका फैसला होना बाकी है।
हम दो अलग-अलग तरीकों से जानने की कोशिश कर सकते हैं कि दोनों में से कौन बड़ा है।
पहला तरीका - चित्रों की सहायता से 4/5 तथा 5/6 में से बड़े भिन्न का पता लगाना।
हम देख सकते हैं कि तुलना तो सम्भव है लेकिन मामला बहुत करीबी बन रहा है। यदि एकदम सही नाप-जोख करके चित्र न बनाया जा सका तो बड़े-छोटे का पता लगा पाना काफी मुश्किल होगा। अत: अब रोटियों के बराबर बँटवारे का तरीका आज़माकर देखते हैं।
यदि शेष बच रहे हिस्सों को भी बराबर बाँट दिया जाए तो 5/6 वाले लोगों को ज़्यादा हिस्सा मिलेगा। अत: 5/6 बड़ा होगा।
दूसरा तरीका - इस तरीके में हम एक रोटी को पूरा करने का प्रयास करेंगे। 4/5 में 1/5 जोड़ने पर 1 रोटी पूरी होती है। इसी तरह 5/6 में 1/6 जोड़ने पर 1 रोटी पूरी होती है।
रोटियों के बराबर बँटवारे के दौरान हमने शुरु में ही सीखा है कि जब एक रोटी ज़्यादा लोगों में बँट रही होगी तो टुकड़ों का आकार छोटा होगा। अत: 1/5 और 1/6 को देखकर ही हम जान सकते हैं कि 1/5 बड़ा होगा। इससे यह मतलब भी निकाला जा सकता है कि जिस टुकड़े को पूरी रोटी बनाने के लिए बड़ा टुकड़ा जोड़ना पड़ रहा है वह टुकड़ा असल में छोटा होगा।
अत: 4/5 और 5/6 में बड़ा भिन्न 5/6 ही होगा। अब हम भिन्न संख्याओं को बढ़ते क्रम में जमा सकते हैं।
1/4 < 1/3 < 3/7 < 1/2 < 4/5 < 5/6 < 9/8
कक्षा 6 - कुछ अनुभव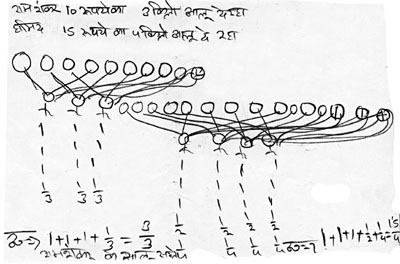 
मैंने एक सरकारी स्कूल की कक्षा छठवीं के बच्चों के साथ ऊपर बताए गए बराबर बँटवारे के तरीके से भिन्न सिखाने पर काम किया था। कई बच्चों ने बँटवारे के तरीके से बनी भिन्न संख्याओं की समझ का इस्तेमाल सवालों को हल करने के लिए किया। शुरु में चित्रों की सहायता से वे बड़े छोटे भिन्न की पहचान कर पा रहे थे, लेकिन आगे चलकर वे बिना चित्र बनाए ही बड़े भिन्न को बता पा रहे थे। कई बच्चे अब समतुल्य भिन्न भी बनाने लगे थे। उनके लिए समतुल्यता का बोध, हर को बराबर करने का गुलाम नहीं था बल्कि उसके पीछे भिन्न की मात्रात्मक समझ थी।
ऊपर दिए हल में सलमान लिखकर बता रहा है कि टोली ॠ में 17 बच्चे हैं और 18 पराठे हैं तो सबको एक से अधिक पराठे मिल जाएँगे जबकि टोली ए में 20 बच्चे हैं और 19 पराठे हैं तो सभी को एक से कम पराठे मिल पाएँगे। दिनेश ने भी इसी तरह के बँटवारे को अपने चित्र में दिखाया है। पहले वह 17 बच्चों को एक-एक पराठा दे रहा है फिर 18वें पराठे के 17 टुकड़े करके सबमें बाँट रहा है। इस तरह सभी को एक से थोड़ा ज़्यादा पराठा मिल रहा है। जबकि दूसरी टोली के 19 बच्चों को वह पहले एक-एक पराठा दे रहा है लेकिन 20वाँ बच्चा अभी खाली हाथ है तो सभी 19 बच्चे अपने-अपने पराठे से थोड़ा हिस्सा उसे दे रहे हैं।
अनुपात की ओर बढ़ चले कदम
रोटियों के बँटवारे का यह तरीका बच्चों के लिए कितना मददगार हो सकता है इसे हम नीचे के कुछ उदाहरणों में देखेंगे। बच्चे कई अलग-अलग सन्दर्भों में भी इसे इस्तेमाल कर पा रहे हैं।
प्रश्न 1 - काजल ने 3 गिलास पानी में 7 चम्मच शक्कर डाली जबकि राहुल ने 5 गिलास पानी में 11 चम्मच शक्कर डाली। किसका शर्बत ज़्यादा मीठा होगा?
अंजना ने पानी के गिलास को रोटी तथा शक्कर की चम्मच को बच्चे के रूप में माना है। पहले 6 बच्चों को आधी रोटी मिली और सातवाँ बच्चा अभी खाली हाथ है जिसे सभी बच्चों ने अपनी आधी रोटी में से थोड़ा हिस्सा तोड़कर दिया। यद्यपि कक्षा के सभी बच्चों ने पानी के गिलास को बच्चे और शक्कर की चम्मच को रोटी मानकर आसान-सा बँटवारा किया। अंजना इसके उलट शुरुआत करते हुए भी यह समझ बना पाई कि काजल की आखिरी चम्मच 3 गिलास में बँट रही है जबकि राहुल की आखिरी चम्मच, 5 गिलास में जा रही है।
प्रश्न 2 - कालू ने सात लीटर दूध में चार लीटर पानी डाला जबकि महेन्द्र ने नौ लीटर दूध में पाँच लीटर पानी डाला। किसका दूध ज़्यादा अच्छा है?
हम देख सकते हैं कि प्रियंका ने चित्र के साथ-साथ समतुल्य भिन्न बनाने का प्रयास भी किया है।
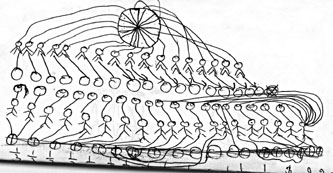प्रश्न 3 - कालू ने पाँच किलो भटे में तीन सौ ग्राम मिर्च डाली जबकि प्रीतम ने तीन किलो भटे में दो सौ ग्राम मिर्च डाली। किसका भरता ज़्यादा चिरका (तीखा) होगा?
सुभाष ने एक किलो भटे को एक रोटी तथा सौ ग्राम मिर्च को एक बच्चे के रूप में माना है। इस तरह कालू के भरते में सौ ग्राम मिर्च में डेढ़ किलो से ज़्यादा भटे जाएँगे जबकि प्रीतम के भरते में सौ ग्राम मिर्च में डेढ़ किलो भटे डाले जा सकेंगे। इसलिए प्रीतम का भरता ज़्यादा चिरका होगा।
प्रश्न 4 - रामशंकर 10 रुपए के 3 किलो आलू बेचता है जबकि हामिद 15 रुपए के 4 किलो आलू बेचता है। बताओ किसके आलू सस्ते होंगे?
यहाँ पर वर्षा एक रुपए को एक रोटी तथा एक किलो आलू को एक बच्चा मान रही है। रामशंकर के लिए बने चित्र में एक बच्चे को तीन पूरी रोटियाँ तथा एक तिहाई रोटी मिल रही है जबकि हामिद के लिए बने चित्र में एक बच्चे को तीन पूरी रोटियाँ, आधी रोटी और चौथाई रोटी मिल रही हैं। स्पष्ट है कि रामशंकर के एक किलो आलू 3 रुपए से कुछ अधिक में मिल रहे हैं जबकि हामिद के एक किलो आलू रुपए से भी अधिक के पड़ रहे हैं। इस तरह रामशंकर के आलू सस्ते हैं।
स्ट्रीफलैंड ने ‘बराबर बँटवारे’ द्वारा भिन्न सिखाने के तरीके पर आधारित अपने लेखों में अँग्रेज़ी के दो शब्दों anchoring context का प्रयेाग किया है। इसका मतलब है एक ऐसा सन्दर्भ जो बच्चों को विषयवस्तु के साथ जुड़ाव बनाने में मदद करे। उनकी बात सोलह आने सही है। ये सन्दर्भ एक बहुत ही मज़बूत तथा उपयोगी anchor (जुड़ाव बनाने वाला) की भाँति ही काम कर रहा है। बच्चे भिन्न संख्याओं से न सिर्फ पुख्ता जुड़ाव बना सके हैं बल्कि विभिन्न स्वरूपों में उनका इस्तेमाल भी कर पा रहे हैं। कम-से-कम मेरी कक्षाओं के अनुभव से मैं यह बात दावे से कह सकता हँू कि अब बच्चों को भिन्न सिखाना उनके और अपने सिर पर भारी बोझ रखने जैसा नहीं है।
मो. उमर: एकलव्य, होशंगाबाद में गणित समूह में कार्यरत हैं। नाटक निर्देशन में विशेष रुचि। यह लेख उनके द्वारा भिन्न पर शिक्षा सत्र, 2008-09 में किए गए शोध का नतीजा है।