पृथ्वी का द्रव्यमान मापने वाला व्यक्ति

लेखक :  आइज़ेक एसीमोव
अनुवाद: डॉ. मनीषा शर्मा

विराट क्रियाकलापों के समाधान हमेशा प्रेरणा की कौंध “यूरेका!” या आकस्मिक खोज के झटके की बजाय कभी-कभी प्रयोगशाला में किसी सम्बन्धित छोटी गतिविधि के बहुत ही सावधानीपूर्वक किए गए मापन से क्षण भर में प्राप्त होते हैं।

कुछ दिनों पहले मैं एक रात्रिभोज में गया था जहाँ एक भद्र महिला, जिन्हें मैं जानता नहीं था, मुझे एक कोने में ले गईं और मुझे नहीं मालूम कि किस वजह से वे मुझे अपने बेटे की विविध उपलब्धियों के बारे में काफी विस्तार से बताने लगीं।
अब ऐसा है कि जब भी चर्चा का विषय मेरे अलावा। कुछ और होता है तो मैं बहुत थोड़ी देर ही एकाग्रचित रह पाता हूँ और इसलिए अधीर होकर मैंने कोई सवाल पूछकर बातचीत के प्रवाह को तोड़ने की कोशिश की।
पहला सवाल जो मुझे सूझा, “और क्या यह प्रशंसनीय युवक आपका इकलौता बेटा है?”
इसके जवाब में महिला ने बड़े उत्साह से कहा, “अरे नहीं! मेरी एक बेटी भी है।”
आखिरकार, यह प्रश्न सार्थक साबित हुआ। वह महिला नहीं समझ सकी कि इस पर मैं क्यों खिलखिलाकर हँस पड़ा; यहाँ तक कि मेरे समझाने के बाद भी वे अपने दिए गए उत्तर की हास्यपूर्ण विसंगति को नहीं समझ पाईं थीं।
स्वाभाविक रूप से इस स्थिति का रस सिर्फ इसमें नहीं था कि उस महिला ने मेरी बात नहीं सुनी (जो किसी के साथ भी हो सकता था), बल्कि मुझे लगा कि यह इस बात को भी सटीक ढंग से दर्शाता था कि किस तरह से पुरानी पारम्परिक सोच ब्रम्हाण्ड को समझने में आड़े आती है।

उदाहरण के तौर पर पूर्व-औद्योगिक समाज में नर शिशु, मादा शिशु से कहीं अधिक मूल्यवान होते थे। शिशु लड़के बड़े होकर पुरुष बनते थे और इसलिए उनमें आगे चलकर खेती या सेना में निहायत ज़रूरी मददगार बनने की सम्भावना देखी जाती थी। जबकि शिशु कन्याएँ बड़ी होकर निरीह औरतें बनती थीं जिनकी काफी खर्चा उठाकर शादी करनी पड़ती थी। फलस्वरूप तब लड़कियों को नज़रअन्दाज़ करते हुए ‘बच्चे’ शब्द को ‘लड़के’ का पर्याय मानने की व्यापक प्रवृत्ति थी।

मेरे खयाल से यह रवैया अभी भी जारी है। हालाँकि यह भी हो सकता है कि ऐसे रुख वाले व्यक्ति को इसका अहसास न हो और जब उस पर इस दृष्टिकोण का आक्षेप लगाया जाए तो वह उग्र होकर इससे साफ इन्कार करे। मुझे लगता है कि जब उस भली महिला ने ‘आपका इकलौता बेटा’, ये शब्द सुने तो वे इनके और ‘आपका इकलौता बच्चा’ के बीच सच में ही कोई अन्तर नहीं समझ पाईं और उन्होंने उसी के अनुरूप उत्तर दिया।

भार का क्या है मतलब
इन सबका इस लेख से क्या लेना-देना है? असल में वैज्ञानिकों की भी ऐसी ही समस्याएँ होती हैं और आज भी वे स्वयं को सोच के पुराने पड़ चुके तरीकों से एकदम पूरी तरह से मुक्त नहीं कर पाते।
उदाहरण के लिए, हम सभी को लगता है कि हम जानते हैं कि हमारा क्या तात्पर्य होता है जब हम किसी वस्तु के ‘भार’ की बात करते हैं, और हम सबका यह ख्याल होता है कि हमें पता है कि हमारा क्या अर्थ है जैसे जब हम कहते हैं कि हम किसी चीज़ को तौल रहे हैं, या एक वस्तु दूसरी वस्तु से ‘भारी’ या ‘हल्की’ है।

परन्तु मैं बिलकुल आश्वस्त नहीं हूँ कि हम सचमुच में यह जानते हैं। यहाँ तक कि भौतिकशास्त्री, जिन्हें पूरी तरह से ज्ञात है कि भार वाकई में क्या है और जो उसे ठीक-ठीक परिभाषित कर सकते हैं तथा समझ सकते हैं, वे भी यदि सावधान न रहें तो त्रुटिपूर्ण तरीकों से सोचने की प्रवृत्ति के शिकार हो सकते हैं।
अपनी बात को थोड़ा स्पष्ट करना चाहूँगा। किसी भी गुरुत्वाकर्षण क्षेत्र की अनिवार्य प्रतिक्रिया है त्वरण। उदाहरण के लिए किसी स्थूल वस्तु के अचानक अन्तरिक्ष में प्रकट होने की कल्पना कीजिए जिसमें उस क्षण (समीप के किसी विशाल खगोलीय पिण्ड के सापेक्ष) कोई त्वरण न हो। उस पिण्ड के सापेक्ष या तो वह गतिहीन हो या स्थिर वेग से गति कर रही हो।

यदि अन्तरिक्ष में उस बिन्दु पर कोई गुरुत्वाकर्षण क्षेत्र न हो जहाँ वस्तु प्रकट हुई हो तो वस्तु या तो विश्राम की स्थिति में बनी रहेगी या स्थिर वेग से गति करती रहेगी। पर अगर उस बिन्दु पर गुरुत्वाकर्षण क्षेत्र हो जैसा कि समीप के उस विशाल खगोलीय पिण्ड के कारण वहाँ होगा तो वस्तु की गति त्वरित होने लगती है। वह या तो क्रमश: तेज, या क्रमश: धीमी होती जाती है, या वस्तु अपनी गति की मूल दिशा से हटते हुए वक्राकार ढंग से मुड़ती जाती है, या इन प्रभावों में से किन्हीं के संयोजन के रूप में गति करती है।

किसी भी ब्रम्हाण्ड में जिसमें थोड़ा भी पदार्थ हो, सभी बिन्दुओं पर गुरुत्वाकर्षण क्षेत्र विद्यमान होता ही है भले वह कितना भी कमज़ोर क्यों न हो, इसलिए अन्तरिक्ष में सभी ऐसे पिण्डों के लिए जो केवल गुरुत्वाकर्षण क्षेत्र के प्रभाव में होते हैं, त्वरण सहित गति सामान्य बात है, जबकि अत्वरित गति ऐसी आदर्श स्थिति है जिसे यथार्थ में हासिल नहीं किया जा सकता।

निश्चय ही, यदि दो वस्तुएँ बिलकुल एक ही प्रकार से किसी तीसरे पिण्ड के सापेक्ष त्वरित गति कर रही हों तो वे दोनों वस्तुएँ एक-दूसरे के सापेक्ष विश्राम की स्थिति में प्रतीत होती हैं। पृथ्वी के सापेक्ष आप खुद को विश्राम की स्थिति में पाते हैं, पर ऐसा इसलिए है क्योंकि आप और पृथ्वी, दोनों सूर्य के गुरुत्वाकर्षण क्षेत्र की प्रतिक्रिया के रूप में बिलकुल एक जैसे ढंग से त्वरित हो रहे हैं।

पर तब आपका और पृथ्वी के गुरुत्वाकर्षण क्षेत्र का क्या रिश्ता है? आप पृथ्वी के सापेक्ष विश्राम की स्थिति में हो सकते हैं, पर मान लीजिए कि अचानक आप के पाँव के नीचे एक सुरंगनुमा छेद बन जाता है। उसी क्षण आप पृथ्वी के गुरुत्वाकर्षण क्षेत्र के प्रभाव में नीचे की ओर त्वरित होने लगेंगे।

आमतौर पर यदि आप ऐसा नहीं करते हैं तो इसका एकमात्र कारण यह है कि जिस दिशा में आप गति करते हैं उस दिशा में अत्याधिक घना पदार्थ भरा रहता है और उस पदार्थ के परमाणुओं द्वारा पैदा किए गए विद्युत-चुम्बकीय बल उन परमाणुओं को आपस में बांधकर रखते हैं और आपको गुरुत्वाकर्षण क्षेत्र के बलों के प्रभाव में आने से आसानी से रोक देते हैं।

हालाँकि एक तरह से, किसी गुरुत्वाकर्षण क्षेत्र के प्रभाव के फलस्वरूप यदि किसी स्थूल वस्तु को त्वरण के साथ गति करने से रोका जाएगा तो वह भी ऐसा ही करने की ‘कोशिश’ करती।। जिस दिशा में वह गति करना ‘चाहती’ है उस दिशा में वह ज़ोर लगाएगी। गुरुत्वाकर्षण के प्रभाव में त्वरण सहित गति करने का यह ‘प्रयास’ ही है जो बल के रूप में सामने आता है और यही वह बल है जिसे हम माप सकते हैं तथा भार कहते हैं।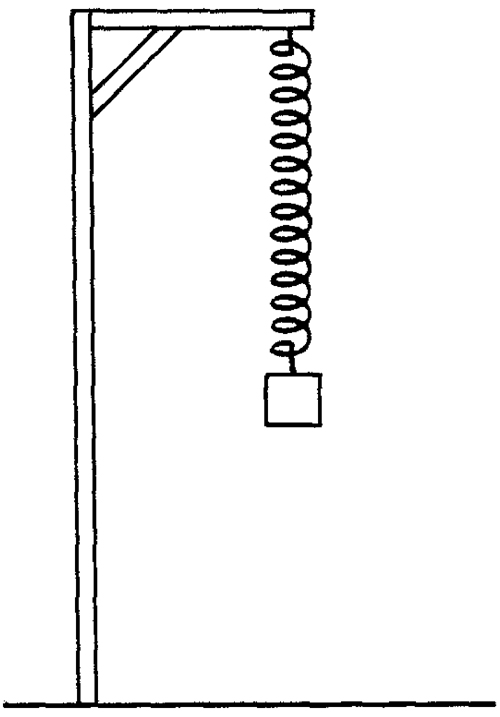

स्प्रिंग पर लटकती वस्तु
मान लीजिए कि हम बल को मापने के लिए छल्लेदार स्प्रिंग का उपयोग करते हैं। यदि हम इस स्पिं्रग को खींचते हैं तो स्प्रिंग लम्बी हो जाती है। यदि हम इसे दोगुने बल से खींचते हैं, तो वह दोगुनी लम्बी हो जाएगी। स्प्रिंग की प्रत्यास्थता (elasticity) की सीमा के भीतर, स्प्रिंग की लम्बाई में प्रसार, बल की तीव्रता के अनुपात में होता है।
अब यदि आप स्पिं्रग के एक छोर को छत की बीम से बांध दें और स्प्रिंग के दूसरे छोर से किसी स्थूल वस्तु को लटका दें तो स्प्रिंग की लम्बाई उतनी ही बढ़ेगी जितना कि उस पर बल लगाया गया है। वह स्थूल वस्तु नीचे की ओर त्वरण करने की ‘कोशिश’ करती है और इस ‘प्रयास’ के परिणामस्वरूप जो बल उत्पन्न होता है वह स्प्रिंग को लम्बा कर देता है।
यदि ऐसी वस्तुओं द्वारा स्प्रिंग की लम्बाई में वृद्धि कराई जाए जिनका भार हम स्वतंत्र ढंग से कहीं किसी मानक भार के अनुसार मालूम कर चुके हों तो उस वृद्धि को नोट करके हम स्प्रिंग को चिन्हांकित (केलिब्रेट) कर सकते हैं। एक बार जब यह सब हो जाता है तो हम लम्बी हो रही स्प्रिंग से जुड़े संकेतक द्वारा स्केल पर दिखाई जाने वाली संख्या के रूप में किसी भी वस्तु के भार को पढ़ सकते हैं।

भार की आम अवधारणा
यहाँ तक ठीक है, लेकिन अपने सबसे आदिम रूप में भार की हमारी धारणा हमारे उस एहसास से निकली है जो हमें तब होता है जब कोई वस्तु हमारे हाथ या हमारे शरीर के किसी अन्य भाग पर विश्राम की स्थिति में होती है और हमें उसे पृथ्वी के गुरुत्वाकर्षण क्षेत्र के सापेक्ष अचल बनाए रखने के लिए मांसपेशियों का ज़ोर लगाना पड़ता है। चूँकि हम पृथ्वी के गुरुत्वाकर्षण क्षेत्र को पहले से ही स्थाई मानकर चलते हैं और कभी भी उसमें किसी महत्वपूर्ण परिवर्तन का अहसास नहीं करते, अत: हम भार की अनुभूति को पूरी तरह से वस्तु का गुण मान लेते हैं।

हम सोचते हैं कि कोई वस्तु भारी है क्योंकि भारी होना उसकी प्रकृति है; बस इतनी-सी बात है। हम इस सोच के इतने आदी हो चुके हैं कि उसके विपरीत जाने वाले प्रत्यक्ष प्रमाण भी हमें विचलित नहीं करते। द्रव में डुबाई गई वस्तु का भार घट जाता है क्योंकि वस्तु पर गुरुत्वाकर्षण क्षेत्र द्वारा नीचे की ओर लगाए गए बल में से वस्तु पर द्रव के द्वारा ऊपर की ओर लगाया गया उत्प्लावन बल घट जाता है। यदि उत्प्लावन बल काफी अधिक हो तो वस्तु तैरेगी। द्रव जितना अधिक घना होता है उतना ही अधिक उसका उत्प्लावन बल होता है। इस प्रकार लकड़ी पानी में तैरेगी और लोहा पारे में तैरेगा।

वास्तव में, हम लोहे के गोले को खुली हवा की तुलना में पानी के अन्दर हल्का महसूस कर सकते हैं, फिर भी हम इसे नकार देते हैं। हम भार को ऐसे बल के रूप में नहीं देखते जो दूसरे बलों द्वारा काटा जा सकता है। हमारा ज़ोर भार को पदार्थ का आन्तरिक गुणधर्म मानने पर होता है और जब कुछ विशिष्ट परिस्थितियों में भार घटकर शून्य रह जाता है तो हम चकित रह जाते हैं, और हम अन्तरिक्ष यात्रियों की भारहीन कूद-फांद को प्रकृति के एकदम विपरीत होने वाली घटना की तरह देखते हैं, और खबर गढ़ने वाले भी ‘वे गुरुत्व की पहुँच से परे हैं’ जैसी बेतुकी बातें कहते हैं।

भार और द्रव्यमान
यह सही है कि आंशिक रूप से भार वस्तु में अन्तर्निहित एक निश्चित गुण पर निर्भर करता है, पर साथ ही वह उस गुरुत्वाकर्षण क्षेत्र की तीव्रता पर भी निर्भर करता है जिसके प्रभाव में वस्तु होती है। यदि हम चन्द्रमा की सतह पर खड़े होते और अपने हाथ में किसी वस्तु को पकड़े होते, तो वह वस्तु वहाँ के गुरुत्वाकर्षण क्षेत्र के प्रति उत्तरदायी होने का ‘प्रयास’ करेगी जिसकी तीव्रता पृथ्वी की सतह पर कार्य कर रहे गुरुत्वाकर्षण क्षेत्र की तीव्रता का केवल छठवाँ भाग ही है।
पदार्थ का वह अन्तर्निहित गुणधर्म क्या है जिस पर भार आंशिक रूप से निर्भर करता है? वह है ‘द्रव्यमान’ - एक विशेष पारिभाषिक शब्द और अवधारणा जिसे न्यूटन ने प्रस्तुत किया।

गुरुत्वाकर्षण क्षेत्र का प्रति-उत्तर देने का ‘प्रयास कर रही’ वस्तु के द्वारा उत्पन्न बल, उसके द्रव्यमान तथा गुरुत्वाकर्षण क्षेत्र की तीव्रता के अनुपात में होता है। यदि गुरुत्वाकर्षण क्षेत्र अपनी तीव्रता में हमेशा एक-सा रहता है (जैसा कि सभी अभिप्रायों और उद्देश्यों के लिए पृथ्वी के गुरुत्वाकर्षण क्षेत्र के बारे में कहना सही होगा, बशर्ते हम पृथ्वी पर या उसकी सतह के नज़दीक रहें), तो हम उस क्षेत्र को नकार सकते हैं। हम तब कह सकते हैं कि सामान्य परिस्थितियों में पृथ्वी के गुरुत्वाकर्षण क्षेत्र के प्रभाव में प्रतिक्रिया करने का ‘प्रयास’ कर रही वस्तु द्वारा उत्पन्न बल उसके द्रव्यमान का समानुपाती होता है।

चूँकि किन्हीं भी साधारण परिस्थितियों में भार और द्रव्यमान परस्पर समानुपाती होते हैं, अत: इन दोनों को समानार्थी मानने का ज़बरदस्त मोह होता है। जब सबसे पहले द्रव्यमान की धारणा स्थापित हुई, तो उसे भी गणना के लिए वे ही इकाइयाँ (उदाहरण के लिए ‘पाउण्ड’) दे दी गईं जिन्हें पहले भार के लिए इस्तेमाल किया जाता था। आज भी हम कहते हैं कि ‘दो किलो का द्रव्यमान’ और ‘दो किलो का भार’, लेकिन यह गलत है। किलोग्राम जैसी इकाइयाँ केवल द्रव्यमान के लिए प्रयोग की जाना चाहिए और भार को बल की इकाइयाँ दी जाना चाहिए। लेकिन इसकी वकालत करना तो ऐसा है जैसे दीवारों से बातें करना।
इकाइयाँ इस प्रकार निर्धारित की गई हैं कि पृथ्वी की सतह पर छ: किलोग्राम के द्रव्यमान वाली वस्तु का भार भी छ: किलोग्राम होता है, पर चन्द्रमा की सतह पर उसी वस्तु का द्रव्यमान छ: किलोग्राम होगा और भार केवल एक किलोग्राम होगा।

पृथ्वी के चारों ओर चक्कर लगा रहा कोई उपग्रह उसके सापेक्ष मुक्त पतन में है और पहले से ही पूरी तरह से पृथ्वी के गुरुत्वाकर्षण क्षेत्र के प्रभाव में सक्रिय है। उसके लिए आगे ‘प्रयास’ करने के लिए कुछ बाकी नहीं है। इसलिए उपग्रह पर छ: पाउण्ड के द्रव्यमान का भार शून्य पाउण्ड होता है और यही सभी वस्तुओं के लिए सत्य है, भले ही वे कितनी ही विशाल क्यों न हों। अत: चक्कर लगा रहे उपग्रह पर वस्तुएँ भारहीन होती हैं। (निश्चित ही चक्कर लगाते हुए उपग्रह पर वस्तुएँ, स्वयं उस उपग्रह के और उस पर उपस्थित अन्य वस्तुओं के गुरुत्वाकर्षण क्षेत्रों के सापेक्ष प्रतिक्रिया करने का ‘प्रयास’ करती हैं, पर ये क्षेत्र इतने नगण्य होते हैं कि उनकी उपेक्षा की जा सकती है।)

क्या इस बात से कोई फर्क पड़ता है कि पृथ्वी की सतह पर भार और द्रव्यमान के जिस नज़दीकी रिश्ते के हम आदी हैं वह अन्य जगह काम नहीं करता? निश्चित ही इससे फर्क पड़ता है। किसी वस्तु का जड़त्व, अर्थात वह बल जो उसे त्वरित करने के लिए ज़रूरी होता है, पूरी तरह से वस्तु के द्रव्यमान पर निर्भर करता है। एक धातु की विशाल छड़ की स्थिति को कुशलता से बदलना (जब वह विश्राम की स्थिति में हो तो उसे गति देना या जब गति कर रही हो तो उसे रोकना) चन्द्रमा पर भी उतना ही कठिन होता है जितना कि पृथ्वी पर, यद्यपि चन्द्रमा पर उसका भार काफी कम होता है। अन्तरिक्ष केन्द्र पर भी चीज़ों को कुशलतापूर्वक इधर-उधर करने में वैसी ही कठिनाई होती है, यद्यपि वहाँ भार तकरीबन शून्य हो जाता है।
अन्तरिक्ष यात्रियों को अत्यन्त सावधान रहना पड़ता है और यदि वे पृथ्वी पर उपजी धारणाओं से मुक्ति नहीं पाते तो वे मर भी सकते हैं। यदि आप तेज़ी से घूम रही दो छड़ों के बीच फँस जाएँ, तो आप पिचक जाएँगे भले ही वे छड़ें भारहीन हैं। आप उन्हें उँगली के हल्के झटके से रोक नहीं पाएँगे यद्यपि उनका भार किसी पंख से भी कम है।

द्रव्यमान का मापन
हम द्रव्यमान को कैसे माप सकते हैं? एक तरीका है कि इस प्रकार के तराज़ू का उपयोग करें जिसमें दो पलड़े एक केन्द्रीय आलम्बक (fulcrum) की धुरी पर घूम रहे होते हैं। मान लीजिए कि अज्ञात भार वाली किसी वस्तु को बाएँ पलड़े में रखा जाता है, तो बायाँ पलड़ा नीचे जाता है और दायाँ ऊपर उठता है।
इसके बाद, मान लीजिए कि दाएँ पलड़े पर क्रमश: धातु की नन्हीं छिलपियाँ रखी जाती हैं जिनमें से प्रत्येक का भार ठीक एक ग्राम है। जब तक कि रखी गई सभी छिलपियों का कुल भार अज्ञात वस्तु से कम होता है तब तक दायाँ पलड़ा उठा रहता है। जब छिलपियों का समग्र भार अज्ञात वस्तु के भार से ज़्यादा हो जाता है तो दायाँ पलड़ा नीचे जाता है और बाँया पलड़ा ऊपर उठता है। जब दोनों पलड़े एक ही तल पर सन्तुलित हो जाते हैं, तो दोनों भार बराबर होते हैं और आप कह सकते हैं कि अज्ञात वस्तु का भार (मिसाल के लिए मान लीजिए) बहत्तर ग्राम है।

लेकिन इस समय दोनों भार एक साथ गुरुत्वाकर्षण क्षेत्र के प्रभाव के अधीन होते हैं और उन पर उस क्षेत्र का प्रभाव आपस में निरस्त हो जाता है। यदि क्षेत्र की तीव्रता बढ़ती या घटती है, तो वह एक साथ दोनों पलड़ों पर एक-सी बढ़ती या घटती है, इसलिए दोनों पलड़ों के सन्तुलन में होने का तथ्य इससे प्रभावित नहीं होता है। उदाहरण के लिए चन्द्रमा पर भी दोनों पलड़े सन्तुलन में रहेंगे। इसलिए सभी उद्देश्यों और अभिप्रायों के लिए इस प्रकार का सन्तुलन एक अन्य गुणधर्म - द्रव्यमान - की माप कर रहा होता है, जिससे भार उपजता है।

वैज्ञानिक भार की बजाय द्रव्यमान को मापना पसन्द करते हैं और इसलिए वे ‘भारी’ और ‘हल्के’ की बजाय ‘अधिक विशाल’ और ‘कम विशाल’ कहने के लिए स्वयं को प्रशिक्षित करते हैं (यद्यपि यह प्रयासपूर्वक और बार-बार गलतियों के साथ ही हो पाता है)।
फिर भी न्यूटन के बाद तीन शताब्दियाँ बीत जाने पर भी अभी तक वे स्वयं को पूरी तरह से न्यूटनपूर्व युग की सोच से मुक्त नहीं कर पाए हैं।

इस स्थिति की कल्पना कीजिए। कोई रसायनशास्त्री एक संवेदनशील रसायनिक तुला का इस्तेमाल करते हुए सावधानीपूर्वक किसी वस्तु का द्रव्यमान मापता है और जैसा हमने वर्णन किया है उसी तरह दोनों पलड़ों को सन्तुलित करता है। उसने क्या किया है? उसने किसी वस्तु का ‘द्रव्यमान मापा’ है। क्या इसे ठीक से कहने का कोई छोटा तरीका है? नहीं, कोई अन्य तरीका नहीं है। भाषा इसमें कोई मदद नहीं करती। वह यह नहीं कह सकता कि उसने वस्तु को ‘द्रव्यमानित’ (मास्ड) किया है, या उसका ‘द्रव्यमानन’ (मासीफाइड या मासीकेटेड) किया है।
जो एकमात्र चीज़ वह कह सकता है वो यह है कि उसने वस्तु को ‘तौला’ (उसका भार मापा) है, और वह यही कहता भी है। मैं भी यही कहता हूँ।
पर किसी वस्तु को तौलना उसके भार को निर्धारित करता है, न कि उसके द्रव्यमान को। अपरिष्कृत अँग्रेज़ी भाषा हमें न्यूटनपूर्व युग तक सीमित रहने पर मजबूर करती है।

फिर से पीछे लौटते हुए, धातु की इन छोटी छिलपियों को, जिनमें प्रत्येक का भार एक ग्राम है, (या कोई अन्य सुविधाजनक परिमाण या विभिन्न प्रकार के परिमाण) ‘मानक द्रव्यमान’ कहा जाना चाहिए यदि हमें यह दर्शाना है कि उनका उपयोग द्रव्यमान मापने के लिए होता है। पर उन्हें यह नहीं कहा जाता। वे ‘भार’ (वेट्स) कहलाते हैं।

पुन:, रसायनशास्त्री को विभिन्न तत्वों के परमाणुओं के सापेक्ष औसत द्रव्यमानों से बार-बार काम पड़ता है। ये सापेक्ष औसत द्रव्यमान सर्वत्र ‘परमाणु भार’ कहलाते हैं। वे भार नहीं हैं, वे द्रव्यमान हैं।
संक्षेप में, चाहे कोई वैज्ञानिक (अपने दिमाग में) कितने भी अच्छे से द्रव्यमान और भार के बीच का अन्तर क्यों न जानता हो, वह (अपने दिल में) तब तक इसे सचमुच में नहीं जान पाएगा जब तक वह ऐसी भाषा का इस्तेमाल करता है जिसमें पुरानी चली आ रही परम्पराएँ बची हुई हैं। उसकी परेशानी उस महिला की तरह ही है जिसे ‘एकमात्र बेटा’ और ‘एकमात्र बच्चा’ में कोई अन्तर नहीं दिखा।

पृथ्वी का द्रव्यमान कितना
चलिए अब आगे बढ़ते हैं। बृहस्पति, पृथ्वी से 318 गुना ज़्यादा विशाल है; सूर्य, पृथ्वी से 3,30,000 गुना विशाल है; चन्द्रमा का आकार पृथ्वी से 1/81 गुना है, इत्यादि।

परन्तु स्वयं पृथ्वी का द्रव्यमान किलोग्राम में क्या है (द्रव्यमान की किसी अन्य इकाई में जिसकी रोज़मर्रा की जानी-पहचानी वस्तुओं के साथ तुलना की जा सके)?
उसे निर्धारित करने के लिए हमें न्यूटन के इस समीकरण का उपयोग करना होगा:

F = GmM/d²              (समीकरण-1)

उदाहरण के लिए यदि इस समीकरण का उपयोग एक गिरते हुए पत्थर के लिए किया जाए, तो F वह गुरुत्वाकर्षण बल है जिसके परिणामस्वरूप पत्थर नीचे की ओर त्वरित हो रहा है, G सार्वभौमिक गुरुत्वाकर्षण स्थिरांक है, m पत्थर का द्रव्यमान है, M पृथ्वी का द्रव्यमान है और d पत्थर के केन्द्र से पृथ्वी के केन्द्र की दूरी है।
दुर्भाग्यवश इन पाँच राशियों में से अठारहवीं शताब्दी के लोग केवल तीन ही निर्धारित कर सकते थे। पत्थर की मात्रा (m) को आसानी से निर्धारित किया जा सकता था और पृथ्वी के केन्द्र से पत्थर की दूरी (d) ग्रीककाल से ही ज्ञात थी। गुरुत्वाकर्षण बल (f) का निर्धारण उस पत्थर के त्वरण को मापकर किया जा सकता था जिसके साथ वह गुरुत्वाकर्षण क्षेत्र के प्रभाव में गति कर रहा था, और यह गैलीलियो द्वारा किया गया था।
केवल गुरुत्वाकर्षण स्थिरांक G का मूल्य, और पृथ्वी का द्रव्यमान M अज्ञात रह गए। यदि क्र का मूल्य ज्ञात होता तो पृथ्वी के द्रव्यमान की गणना तत्काल की जा सकती थी। इसके विपरीत यदि G ज्ञात होता, तो सार्वभौमिक गुरुत्वाकर्षण स्थिरांक जल्दी से निर्धारित किया जा सकता था।
तो फिर, क्या किया जाए?

पृथ्वी की मात्रा को सीधे निर्धारित किया जा सकता था यदि उसे इधर-उधर किया जा सकता अथवा उसे मानक भारों या ऐसी किसी चीज़ के सामने तराज़ू के पलड़े पर रखा जा सकता। परन्तु पृथ्वी के साथ ऐसा कुछ भी नहीं किया जा सकता, कम-से-कम किसी प्रयोगशाला में इंसान द्वारा तो नहीं, इसलिए इसे भूल जाइए।

फिर क्र के निर्धारण के बारे में क्या किया जा सकता है? यह गुरुत्वाकर्षण स्थिरांक है और यह किसी भी गुरुत्वाकर्षण क्षेत्र के लिए एक समान होता है। इसका मतलब है कि हमें क्र को निर्धारित करने के लिए पृथ्वी के गुरुत्वाकर्षण क्षेत्र का उपयोग करना ज़रूरी नहीं है। हम किसी छोटी वस्तु के गुरुत्वाकर्षण क्षेत्र का उपयोग कर सकते हैं जिसे हम मनचाहे ढंग से इधर-उधर हिला सकते हैं।

उदाहरण के लिए, मान लीजिए कि हम किसी वस्तु को एक स्प्रिंग से लटका देते हैं। पृथ्वी के गुरुत्वाकर्षण क्षेत्र के प्रभाव से स्पिं्रग लम्बा हो जाता है। अब हम गोल पत्थर लेते हैं और उसे लटकती हुई वस्तु के नीचे रखते हैं। पत्थर का गुरुत्वाकर्षण क्षेत्र अब पृथ्वी के गुरुत्वाकर्षण क्षेत्र में जुड़ जाता है और परिणाम स्वरूप स्प्रिंग थोड़ी और लम्बी हो जाती है।
स्प्रिंग की लबाई में अतिरिक्त वृद्धि की मात्रा से हम पत्थर के गुरुत्वाकर्षण क्षेत्र की तीव्रता को निर्धारित कर सकते हैं।
आइए अब हम न्यूटन के समीकरण के निम्नलिखित परिवर्तित रूप का इस्तेमाल करते हैं:

f = Gmm'/ d²                   (समीकरण-2)

जहाँ f पत्थर के गुरुत्वाकर्षण क्षेत्र की तीव्रता है (जो स्प्रिंग की लम्बाई में अतिरिक्त वृद्धि से मापी गई है), G गुरुत्वाकर्षण स्थिरांक है, m स्प्रिंग से लटकाई गई वस्तु का द्रव्यमान है, m" गोल चट्टान का द्रव्यमान है और d पत्थर के केन्द्र से लटकी हुई वस्तु के केन्द्र के बीच की दूरी है।
इन राशियों में से G के सिवाय प्रत्येक परिमाण को निर्धारित किया जा सकता है, अत: हम समीकरण-2 को इस प्रकार लिख सकते हैं:

G = fd²/mm'                   (समीकरण-3)

अब हमें क्र का मान मिल सकता है। हम इस मान को समीकरण-1 में क्र के स्थान पर रख सकते हैं और फिर समीकरण-1 को m (धरती का द्रव्यमान) ज्ञात करने के लिए इस तरह से हल कर सकते हैं:

M = Fd²/Gm                   (समीकरण-4)

परन्तु इसमें एक पेंच है। द्रव्यमान की तुलना में गुरुत्वाकर्षण क्षेत्र अविश्वसनीय रूप से इतने कमज़ोर होते हैं कि आसानी से मापे जा सकने वाले पर्याप्त तीव्र गुरुत्वाकर्षण क्षेत्र के लिए बहुत विशाल वस्तु की ज़रूरत होती है। स्पिं्रग से लटकती हुई वस्तु के नीचे रखे हुए गोल पत्थर से स्प्रिंग की लम्बाई में इतनी अतिरिक्त बढ़त पैदा ही नहीं होगी कि उसे मापा जा सके। तो यही है वह पेंच।
गुरुत्वाकर्षण क्षेत्र को और तीव्र करने का अन्य कोई तरीका नहीं है, अत: किसी अत्यन्त संवेदनशील उपकरण का प्रयोग करने में ही पृथ्वी के द्रव्यमान की समस्या सुलझाने की कोई सम्भावना बनती थी। कुछ इस तरह के उपकरण की ज़रूरत थी जो प्रयोगशाला में काम करने योग्य पर्याप्त छोटी वस्तु द्वारा उत्पन्न सूक्ष्म गुरुत्वाकर्षण क्षेत्र और इस क्षेत्र के द्वारा पैदा किए गए सूक्ष्म बल को माप सके।

ऐंठन तुला और हैनरी कैवेन्डिश
ऐसे सूक्ष्म मापन के लिए ज़रूरी उपकरण सन् 1777 में सुलभ हुआ जब फ्रांसीसी भौतिकशास्त्री चार्ल्स ऑॅगस्टीन कूलम्ब और साथ ही (स्वतंत्र रूप से) अँग्रेज़ भूवैज्ञानिक जॉन मिशेल ने ‘ऐंठन तुला’ (टॉर्शन बैलेंस) का आविष्कार किया।
बल द्वारा किसी स्प्रिंग को लम्बा करने या किसी आलम्बक के सहारे पलड़ों को ऊपर-नीचे खींचने की बजाय ऐंठन तुला में बल का उपयोग किसी डोरी या तार को ऐंठने या मरोड़ने के लिए होता था।
यदि स्प्रिंग या तार बहुत ही बारीक हो तो उसे काफी सारा ऐंठने के लिए छोटे-से बल की आवश्यकता होगी। ऐंठन का पता करने के लिए ऊर्ध्वाधर तार से एक लम्बी क्षैतिज छड़ को इस तरह जोड़ना पड़ता है कि वह मध्य बिन्दु पर सन्तुलित हो। अब एक छोटी-सी ऐंठन भी छड़ के छोरों पर एक विस्थापन पैदा करती है।
यदि एक बेहद पतले तार और लम्बी छड़ का उपयोग किया जाए तो ऐंठन तुला को बहुत ही संवेदनशील बनाया जा सकता है। इतना कि वह किसी सामान्य वस्तु के गुरुत्वाकर्षण क्षेत्र को भी पकड़ सके।

सन् 1798 में अँग्रेज़ रसायनशास्त्री हैनरी कैवेन्डिश ने ऐंठन तुला के सिद्धान्त का उपयोग क्र के मान को मालूम करने में किया।
मान लीजिए कि आप एक छ: फीट लम्बी छड़ लेते हैं और उसके प्रत्येक सिरे पर एक दो इंच व्यास वाली सीसे की गेंद रखते हैं। इसके बाद आप छड़ के केन्द्र पर एक बारीक तार लपेटकर छड़ को लटका देते हैं।

यदि छड़ के एक छोर पर रखी सीसे की गेंद पर बहुत ही छोटा बल लगाया जाता है और उतनी ही मात्रा का छोटा बल दूसरे छोर पर रखी दूसरी सीसे की गेंद पर लगाते हैं तो क्षैतिज छड़ कुछ घूमती है और जिस तार से छड़ बँधी है वह तार ऐंठने लगेगा। ऐंठता हुआ तार ऐंठन खोलने का ‘प्रयास’ करता है। तार जितने ज़्यादा बल से ऐंठा जाता है ऐंठन खोलने वाला बल उतना ही ज़्यादा ताकतवर हो जाता है। अन्त में ऐंठन खोलने वाला बल, ऐंठन कराने वाले बल को सन्तुलित कर लेता है और छड़ एक नई सन्तुलन की स्थिति में आ जाती है। सीसे की गेंदों पर काम करने वाले बल के परिमाण को छड़ की स्थिति में हुए परिवर्तन की मात्रा से निर्धारित किया जा सकता है।

ज़ाहिर है कि आपको इस पूरी व्यवस्था को एक डिब्बे में बन्द करना पड़ेगा और इस डिब्बे को एक सीलबन्द स्थिर तापमान वाले कमरे में रखना पड़ेगा ताकि तापमान के परिवर्तनों और किन्हीं यांत्रिक हलचलों से उत्पन्न हवा की धाराएँ प्रयोग में कोई बाहरी त्रुटि पैदा न कर सकें।
जब छड़ की स्थिति में केवल थोड़ा-सा परिवर्तन होता है तो इसका अर्थ होता है कि बारीक तार की ज़रा-सी ऐंठन मात्र भी लगाए गए बल को सन्तुलित करने के लिए पर्याप्त विपरीत बल पैदा करती है। वह बताती है कि कितना छोटा बल उस समय लगाया गया - और ठीक यही सूझ कैवेन्डिश के दिमाग में थी।
उन्होंने एक क्षैतिज छड़ के सिरों पर रखी गई छोटी सीसे की गेंदों में से एक गेंद के एक तरफ, एक आठ इंच व्यास वाली सीसे की गेंद को लटकाया। फिर उन्होंने एक वैसी ही दूसरी गेंद को दूसरे छोर पर रखी छोटी गेंद के विपरीत तरफ लटकाया।

बड़ी सीसे की गेंदों का गुरुत्वाकर्षण क्षेत्र अब छड़ को घुमाने का काम करेगा और उसे नई स्थिति में पहुँचा देगा।
कैवेन्डिश ने बार-बार इस प्रयोग को दोहराया और छड़ की स्थिति में बदलाव और इस प्रकार तार की ऐंठन से उन्होंने समीकरण-3 में ढ के मूल्य को निर्धारित किया। चूँकि उन्हें थ्र्, थ्र्" और ड्ड के मूल्य पता थे, वे तत्काल क्र के मूल्य की गणना कर सके।

कैवेन्डिश के द्वारा आकलित मूल्य और आज के मान्य मूल्य, जो 0.0000000000667 मीटर3 / किलोग्राम-सैकेंड2 है, में एक प्रतिशत से भी कम का अन्तर है। (इस इकाई के महत्व के बारे में न पूछें; समीकरण को सन्तुलित करने के लिए यह ज़रूरी होती है)।
एक बार जब हमें क्र का मूल्य दी गई इकाइयों में मिल जाता है तो हम समीकरण-4 को हल कर सकते हैं और यदि हम सही इकाइयों का उपयोग करेंगे, तो तुरन्त ही पृथ्वी का द्रव्यमान किलोग्राम में निकल आएगा। जो मूल्य निकलकर आता है वह है 5,983,000,000,000,000,000,000,000, या 5.983x10²⁴ किलोग्राम। (मोटे तौर पर यदि आप इसे शब्दों में कहना चाहते हैं तो ‘लगभग छ: सैपटिलियन किलोग्राम।’)
अन्य पिंडों का द्रव्यमान निर्धारण
एक बार जब हमें पृथ्वी का द्रव्यमान किलोग्राम में मिल जाता है तो हम अन्य वस्तुओं का द्रव्यमान भी निर्धारित कर सकते हैं, बशर्ते कि पृथ्वी के द्रव्यमान से उनके द्रव्यमान का अनुपात ज्ञात हो।

चन्द्रमा का द्रव्यमान पृथ्वी के द्रव्यमान का 1/81वाँ हिस्सा अर्थात् 7.4x10²² किलोग्राम है। बृहस्पति का द्रव्यमान पृथ्वी के द्रव्यमान से 318 गुना है, यानी कि वह 1.9x10²⁷ किलोग्राम है। सूर्य का द्रव्यमान जो पृथ्वी के द्रव्यमान से 3,30,000 गुना है, वह 2 x 10³⁰ किलोग्राम है।
अत: कैवेन्डिश ने न केवल पृथ्वी के द्रव्यमान को मापा बल्कि उन्होंने (कम-से-कम सम्भावित रूप से) ब्रम्हाण्ड की प्रत्येक अन्य वस्तु के द्रव्यमान को भी, सिर्फ सीसे की छोटी गेंदों के जोड़े की स्थिति में, उनके समीप बड़ी सीसे की गेंदों का जोड़ा रखने से हुए छोटे से परिवर्तन को नोट करके, माप लिया।
इससे पता चलता है कि एक सरल से समीकरण में कितनी ताकत होती है।
परन्तु - जब कोई व्यक्ति कैवेन्डिश की इस चकित कर देने वाली उपलब्धि का उल्लेख करना चाहता है, तो वह क्या कहता है? वह कहता है: ‘कैवेन्डिश ने पृथ्वी को तौला’ - और यही सारी चर्चा का सार बिन्दु है।

यहाँ तक कि भौतिकशास्त्री और खगोलशास्त्री भी कैवेन्डिश के बारे में इसी तरह से बात करते हैं - वह व्यक्ति जिसने ‘पृथ्वी को तौला।’
उन्होंने ऐसी कोई चीज़ नहीं की! उन्होंने पृथ्वी के द्रव्यमान को निर्धारित किया। उन्होंने पृथ्वी को ‘द्रव्यमानित’ किया। यह हो सकता है कि अँग्रेज़ी-हिन्दी भाषा में कोई ऐसी क्रिया न होती हो, परन्तु यह मेरी नहीं उस भाषा की त्रुटि है। मेरे लिए, कैवेन्डिश वह व्यक्ति है जिसने पृथ्वी को ‘द्रव्यमानित’ किया (The Man Who Massed the Earth), चाहे यह अँग्रेज़ी भाषा को अच्छा लगे या न लगे।
इससे अब एक सवाल बाकी रह जाता है: पृथ्वी का भार क्या है?

उत्तर आसान है। पृथ्वी मुक्त रूप से गिर रही है और मुक्त रूप से गिरती हुई किसी भी अन्य वस्तु की तरह, वह जिस गुरुत्वाकर्षण क्षेत्र के प्रभाव में आती है उसके प्रति अपनी पूरी सामर्थ्य से क्रिया करती है। वह आगे और कोई प्रतिक्रिया करने का ‘प्रयास’ नहीं कर रही है और इसलिए वह भारहीन है।
अत: पृथ्वी का भार तब शून्य है।

आइज़ेक एसीमोव: बीसवीं शताब्दी में विज्ञान को लोगों तक पहुँचाने में जिन वैज्ञानिकों का महत्वपूर्ण योगदान रहा है - उनमें से एक हैं आइज़ेक एसीमोव। विज्ञान गल्प को भी वे नईऊँचाइयों तक लेकर गए। उन्होंने बहुत-सी पुस्तकें लिखीं हैं, जिनकी कुल संख्या सैकड़ों में होगी।

अँग्रेज़ी से अनुवाद: डॉ. मनीषा शर्मा: शिक्षा और व्यवसाय से चिकित्सक हैं। विज्ञान और शिक्षा में गहरी दिलचस्पी। अनुवाद करने का शौक है। दिल्ली में रहती हैं।
यह लेख एसीमोव के संकलन ‘द एज ऑफ टुमॉरो’ (The Edge Of Tomorrow) से साभार।