QED: सत्य की तलाश

पुस्तक  अंश

शेषािगरी केएम राव

“हम ज्ञान कहाँ से प्राप्त करते हैं? अवलोकन से। लेकिन अवलोकन तो हम एक-एक प्रकरण का ही कर सकते हैं।...उन उदाहरणों से जिन्हें हमने देखा है। हमें लगता है कि उन उदाहरणों में हमें जो कुछ सत्य प्रतीत हुआ था वह अतीत, वर्तमान और भविष्य के उसी तरह के अन्य मामलों में भी सही होगा चाहे उनकी संख्या कितनी भी हो।”
- जॉन स्टुअर्ट मिल

एक दिन चन्ना ने एकदम सपाट भाव से पूछा, “तुम्हें कैसे पता कि किसी त्रिभुज के तीन कोणों का योग 180 डिग्री होता है? तुम्हें कैसे पता कि यह सत्य है?”  यह पहले सत्र के बाद कक्षा-8 की बात है। सवाल सरल लगता था और जवाब ज़ाहिर था। लेकिन जब उन्होंने यह सवाल पूछा तो मुझे एक शरारती मंशा का भान हुआ। मुझे क्या पता था कि वे हमें एक सफर पर ले जाने वाले हैं जो 2000 से भी ज़्यादा वर्ष पुराना है और युक्लिड नाम के एक इन्सान के साथ शुरू हुआ था।
‘प्रमाण’ शब्द से हमारा पहला सम्पर्क ‘प्रमेय’ शब्द के साथ तब हुआ था जब 1982 के मध्य में हम ज्यामिति सीख रहे थे। तब तक हमने ज्यामिति की कुछ प्रारम्भिक बातें सीखी थीं - विभिन्न किस्म के त्रिभुज कैसे बनाएँ, अज्ञात कोण का पता कैसे लगाएँ, कोणों और रेखाओं को द्विभाजित कैसे करें वगैरह।

चलते-चलते हम यह मानकर चलने लगे थे कि त्रिभुजों का सबसे सामान्य गुण यह होता है कि किसी भी त्रिभुज के तीन कोणों का योग सदा 180 डिग्री होता है। यह तो ब्रह्म वाक्य (अटल सत्य) था।
मैं हमेशा सोचा करता था कि हम 180 डिग्री की इस संख्या पर कैसे पहुँचे। मसलन, 246 डिग्री क्यों नहीं? खैर, तब मैंने यह सवाल नहीं पूछा था और मुझे यह समझने में बरसों लग गए कि हमने सम्पूर्ण कोण के लिए 360 डिग्री, ऋजु कोण (स्ट्रेट एंगल) के लिए 180 डिग्री वगैरह क्यों चुने। अब मेरा मानना है कि पूरा मामला सुविधा का है क्योंकि 360 एक ऐसी संख्या है जिसके गुणनखण्डों की संख्या काफी अधिक है जिसके चलते गणनाएँ आसान हो जाती हैं।
“तुम्हें कैसे पता कि यह सत्य है?” चन्ना अड़े रहे।
हममें से कुछ ने अविलम्ब जवाब दिया, “नापकर देख लीजिए, आपको 180 डिग्री ही मिलेगा।” मुझे याद है कि सवाल सुनकर मैं चौंक गया था। उस समय यह इतना प्रत्यक्ष-सा लगता था। और हमारे कंपास बॉक्स में चाँदे वैसे भी 180 डिग्री दर्शाने के लिए बनाए गए थे। तो कुछ और कैसे हो सकता है? लिहाज़ा, मेरे दिमाग में मामला बन्द था।
“मैं कितने त्रिभुज बनाकर नापूँ?” चन्ना ने जारी रखा।

निगमन यानी डिडक्शन क्यों ज़रूरी?
इस सवाल ने हमें थोड़ा हैरान किया और मुझे याद है हम किसी एक संख्या पर सहमत नहीं हो पाए थे। दरअसल, कोई भी संख्या मनमानी ही होती - 10, 50, 100, 1000...। थोड़ी देर तक कक्षा में सन्नाटा रहा। चन्ना की बात में दम तो था और हम यह कहकर बच नहीं सकते थे कि हम बहुत सारे त्रिभुजों के आँकड़े ले लेंगे। लेकिन मैं सोचता रहा: यदि पहले 1000 त्रिभुजों के कोणों का योग 180 डिग्री हुआ, तो क्या 1001वाँ त्रिभुज अलग हो सकता है?
और, वास्तव में उनका अगला सवाल यही था, “यदि 1001वें त्रिभुज के कोणों का योग 180 डिग्री न हुआ तो?” कक्षा से कोई जवाब नहीं आया। वे कोशिश क्या कर रहे हैं?
चन्ना की बात को थोड़ा और स्पष्ट करने के लिए, एक और उदाहरण मुनासिब होगा। इसे ‘मॉन्स्ट्रस काउंटर एक्ज़ाम्पल’ (विकराल विपरीत उदाहरण) कहते हैं और इससे मेरा परिचय हाल ही में हुआ था। यह उदाहरण दर्शाता है कि गणित नाम की यह चीज़ काफी बेरहम हो सकती है। इस वक्तव्य पर गौर कीजिए: “व्यंजक {1+1141n2}, जहाँ n एक प्राकृत संख्या है, का उत्तर कभी भी एक वर्ग संख्या नहीं होगा।” वर्ग संख्या 25 जैसी कोई संख्या होती है जिसे 5x5 के रूप में लिखा जा सकता है, जहाँ 5 को 25 का ‘वर्गमूल’ कहते हैं। ‘वर्ग’ शब्द का उपयोग इसलिए भी किया जाता है क्योंकि 25 को 5 इकाई गुणा 5 इकाई के एक वर्ग के रूप में भी प्रस्तुत किया जा सकता है। आप ऐसी कई वर्गाकार संख्याएँ जानते होंगे जिन्हें वर्ग कहते हैं।

जब इस व्यंजक की जाँच के लिए कंप्यूटरों का उपयोग किया गया तो पता चला कि 1 से लेकर 30, 693, 385, 322, 765, 657, 197, 397, 207 तक की किसी भी प्राकृत संख्या के लिए इस व्यंजक से वर्ग संख्या नहीं निकली। यह कोई छोटी-मोटी संख्या नहीं है। इतनी संख्याओं से परखने के बाद कोई भी यह निष्कर्ष निकाल लेता कि उक्त व्यंजक {1+1141n2} का उत्तर कभी भी एक वर्गाकार संख्या नहीं होगा। लेकिन - और यह सरासर पागलपन है - व्यंजक ने अगली संख्या के लिए वर्गाकार संख्या उत्पन्न कर दी। तो क्या आप इसके वर्गमूल का हिसाब लगा सकते हैं? विश्वास करना मुश्किल है, नहीं? वाकई हैरतअंगेज़ है। संख्याओं की दुनिया आपको ऐसे ही चौंका सकती है।
मुझे याद है, चन्ना ने कहा था, “इसी वजह से हमें सिद्ध करना होता है कि चाहे जो भी हो जाए, त्रिभुज के तीन कोणों का योग 180 डिग्री ही होगा।” तो हमने इस प्रारम्भिक प्रमेय को सिद्ध किया और साथ में यह सीखा कि प्रमेय और कुछ नहीं, किसी बात का दावा होता है जिसका एक प्रमाण होता है जो तथाकथित ‘निगमन तर्क’ का उपयोग करके तैयार किया गया है।

गणित में यह ऐसा कुछ कहने जैसा होता है कि “यदि A=B है और B=C है तो A=C होगा।” आम बोलचाल में यह कुछ ऐसा होगा: “सारे सेब फल होते हैं, सारे फल पेड़ों पर उगते हैं, इसलिए सारे सेब पेड़ पर उगते हैं।” ज़्यादा पेचीदा मामलों में प्रमाण के हरेक चरण को तार्किक ढंग से अगले चरण तक पहुँचते जाना चाहिए, जब तक कि आप निष्कर्ष तक न पहुँच जाएँ। आप निगमन तर्क के अपने उदाहरण बना सकते हैं। हम ऐसा रोज़ाना करते हैं हालाँकि इसे हर बार पहचानते नहीं। बात सीधी-सी है, नहीं? परन्तु ज़रूरी नहीं कि हर बार ऐसा ही हो। कुछ प्रमेयों के लिए प्रमाण सैकड़ों पन्नों में फैला हो सकता है। जैसे मशहूर ‘फर्मा के अन्तिम प्रमेय’ का प्रमाण 150 पृष्ठ लम्बा है। इसे ‘बीसवीं सदी का सरताज प्रमाण’ कहा गया था। इस पर बाद में बात करते हैं।
मेरे लिए तो यह गणित करने का एक नया तरीका था। हम तो तब तक विभिन्न किस्म की गणनाएँ करने के आदी थे। यह एक नए किस्म का प्राणी था जिसे समझने की ज़रूरत थी। आसान नहीं था। लेकिन हम गणित में सत्य और असत्य में भेद करने की राह में एक महत्वपूर्ण कदम उठा रहे थे।

बुनियाद में स्वयंसिद्ध मान्यताएँ
और बात  इतनी ही नहीं थी। चन्ना अपने दाहिने हाथ को लगातार एक चाप की आकृति में लहरा रहे थे। वे ऐसा तब करते थे जब उन्हें कोई गम्भीर बात कहनी होती थी। उन्होंने कहा, “स्कूल में हमारा सामना जिन तमाम ज्यामितीय प्रमेयों से होता है, जिन्हें लेकर हम इतनी मगजमारी करते हैं, वे सब-के-सब कुछ मूलभूत कथनों पर टिके हैं जिन्हें एक्सियम्स या पॉस्टुलेट्स (स्वयंसिद्ध मान्यता) कहते हैं।” सरल शब्दों में एक्सियम्स वे मूलभूत मान्यताएँ हैं जो स्वयंसिद्ध लगती हैं।
“जो ज्यामिति हम इस समय सीख रहे हैं,” चन्ना ने बताया, “वह कुछ मान्यताओं पर टिकी है जिन्हें युक्लिड नाम के एक व्यक्ति ने 2000 वर्ष पूर्व यूनान में एलेक्ज़ेंड्रिया में स्थापित किया था।” तो, इसे युक्लिडियन ज्यामिति कहते हैं और इसे पुस्तकों की एक ंखला में लिखा गया था। इन पुस्तकों का नाम एलीमेंट्स है। देखा जाए, तो लगभग 2000 वर्षों तक मात्र युक्लिडियन ज्यामिति ही एकमात्र ज्यामिति थी।

युक्लिड को लेकर कई सारे विवाद हैं। कुछ इतिहासकारों को तो सन्देह है कि युक्लिड नाम के किसी व्यक्ति का वजूद भी था। अन्य यूनानी गणितज्ञ प्राय: युक्लिड के नाम का उपयोग भी नहीं करते और मात्र ‘एलीमेंट्स के रचयिता’ की बात करते हैं।
चन्ना ने हमें बताया, “जो ज्यामिति हम सीख रहे हैं, वह मान्यताओं या एक्सियम्स के बगैर ढह जाएगी। उसका कोई अर्थ नहीं होगा और मात्र अफरा-तफरी बचेगी। ये मान्यताएँ शुरुआती बिन्दु (प्रस्थान बिन्दु) हैं जिनके बिना हम किसी कथन को सिद्ध करने की दिशा में नहीं बढ़ पाएँगे।” बातें पहेलियाँ बनती जा रही थीं!
मैं चुपचाप बैठकर सुनता रहा और यह समझने की कोशिश करता रहा कि वे कह क्या रहे हैं। हमने गणित में ऐसी कहानियाँ पहले कभी नहीं सुनी थीं।
दरअसल, आठवीं कक्षा में पहुँचने से पहले हमने कोई कहानी ही नहीं सुनी थी। हम तो बस सवाल ‘छुड़ाने’ के आदी थे। हमारा गणितीय जीवन सरल किन्तु उबाऊ रहा था।

आप शायद सोच रहे होंगे कि माजरा क्या है, तो मैं युक्लिड के पाँच एक्सियम (स्वयंसिद्ध अभिधारणाएँ) पेश कर देता हूँ। फिर हम देखेंगे कि कैसे इनके बगैर हम मुश्किल में फँस जाएँगे। भले मानुस युक्लिड ने एलीमेंट्स में कहा था, “निम्नलिखित को मानकर चलते हैं”:
1. किन्हीं दो बिन्दुओं को जोड़कर एक सरल रेखाखण्ड खींचा जा सकता है।
2. किसी भी सरल रेखाखण्ड को अनन्त तक एक सरल रेखा के रूप में बढ़ाया जा सकता है।
3. किसी भी सरल रेखाखण्ड को त्रिज्या मानकर और उसके एक अन्तिम बिन्दु को केन्द्र मानकर एक वृत्त बनाया जा सकता है।
4. सारे समकोण एक-दूसरे के बराबर होते हैं।
5. यदि एक सरल रेखा दो सरल रेखाओं पर गिरकर अपने एक ही ओर दो अन्त:कोण इस प्रकार बनाए कि इन दो कोणों का योग मिलकर दो समकोणों से कम हो तो वे दो सरल रेखाएँ अनिश्चित रूप से आगे बढ़ाए जाने पर उसी ओर मिलती हैं जिस ओर यह योग दो समकोणों से कम होता है। (इसे ‘समानान्तर अभिधारणा’ कहते हैं और यह मशहूर होने के अलावा विवादास्पद भी है।)
मुझे याद है कि मैं हैरान रह गया था - ऐसी ज़ाहिर-सी बात को कहने की क्या ज़रूरत है? और जैसे मेरे मन की बात ताड़कर ही चन्ना ने कहा था कि ये मान्यताएँ, देखा जाए तो, मान्यताएँ ही हैं। इन पर सवाल नहीं उठाए जा सकते। इन्हें तो इसी रूप में स्वीकार करना होगा। किन्तु ये रोज़मर्रा के अनुभवों और हमारे जीवन के यथार्थ में से उपजती हैं। और जैसा कि हम अभी देखेंगे, ये हमें बहुमूल्य शुरुआती बिन्दु प्रदान करती हैं। युक्लिड मुझे पकाने लगे थे। हम जा कहाँ रहे हैं?
चन्ना ने एक और उदाहरण दिया। उन्होंने कहा कि यह कुछ हद तक शतरंज के खेल जैसा है। रानी आगे-पीछे, आड़े या तिरछे चल सकती है जबकि हाथी सिर्फ आड़ा या खड़ा चल सकता है। हम इस पर सवाल नहीं उठाते। यह एक मान्यता या नियम है जो उस खेल की बुनियाद है। यदि आप इसे बदलते हैं, तो खेल बदल जाता है और आपको शायद एक अलग ही किस्म का शतरंज मिल जाए। तो, नियम स्वयंसिद्ध हैं और हम उन पर सवाल नहीं उठाते। स्वयंसिद्ध मान्यताएँ या अभिधारणाएँ भी ऐसी ही हैं।

प्रमेय सिद्ध करने का एक उदाहरण
युक्लिड की स्वयंसिद्ध मान्यताओं की उपयोगिता को सराहने के लिए सबसे बढ़िया उदाहरण वह प्रमेय है जो कहती है कि किसी भी त्रिभुज (जैसे चित्र-1[i] में त्रिभुज ABC, जिसे प्राय: ∆ABC लिखते हैं) के तीन कोणों का योग 180 डिग्री होता है। आम तौर पर यह पहली प्रमेय होती है जिसे सिद्ध करने का मौका हमें स्कूल में मिलता है।
इस प्रमेय को सिद्ध करने के एक सामान्य तरीके में चित्र-1 में दर्शाए ढंग से ∆ABC को लेकर कुछ रचना करनी पड़ती है। यह आम तरीका है। हमें ये रचनाएँ बनाने की छूट होती है, बशर्ते कि हम मूल आकृति (वर्तमान सन्दर्भ में ∆ABC) को न बदलें। हमने यहाँ जो किया है, जैसा कि चन्ना ने 1982 में किया था, वह इस प्रकार है:
1. बिन्दु A से हमने त्रिभुज के दूसरी ओर वाली भुजा (BC) के समानान्तर एक रेखा खींची। इस समानान्तर रेखा पर हमने दो बिन्दु F और G चिन्हित कर दिए। युक्लिड की समानान्तर मान्यता याद है? हम यहाँ उसका उपयोग करेंगे।

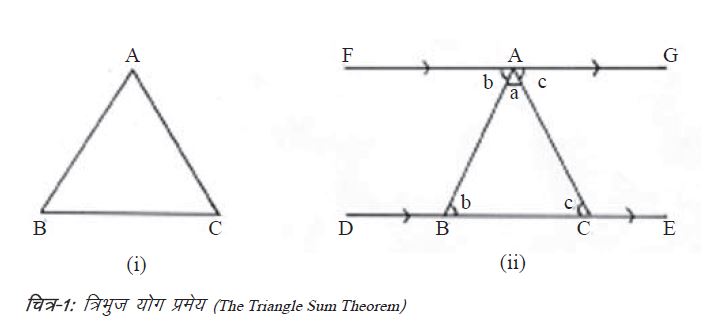
2. हमने भुजा BC को दोनों दिशाओं में आगे बढ़ा दिया और इस विस्तारित रेखा पर दो बिन्दु D और E चिन्हित कर दिए। चित्र-1 से स्पष्ट है कि रेखाएँ FG और DE परस्पर समानान्तर हैं अर्थात् दोनों सिरों से अनिश्चित रूप से बढ़ाए जाने पर वे कभी नहीं मिलेंगी।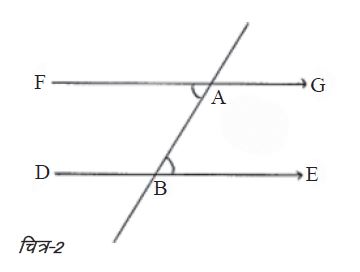

यहाँ तक पहुँचने से पहले हम यह सीख चुके थे कि जब दो समानान्तर रेखाओं को कोई तीसरी रेखा काटती है (जिसे तिर्यक रेखा कहते हैं) तो एकान्तर कोण बराबर होते हैं। इस बात को चित्र-2 में दर्शाया गया है। दो समानान्तर रेखाएँ FG और DE हैं तथा AB तिर्यक रेखा है जो इन दो रेखाओं को काटती है।
दो समानान्तर रेखाओं को काटने वाली कितनी भी तिर्यक रेखाएँ हो सकती हैं। कोण FAB और ABE एकान्तर कोण हैं जो बराबर हैं।

अब हम चित्र-1 पर लौट सकते हैं और देख सकते हैं कि वे कौन-से एकान्तर कोण हैं जो बराबर हैं। इस चित्र में समानान्तर रेखाएँ FG और DE दो तिर्यक रेखाओं AB और AC को काटती हैं। इसका मतलब हुआ कि:
कोण GAC = कोण ACB (चूँकि ये एकान्तर कोण हैं)
इसी प्रकार से कोण FAB = कोण ABC (चूँकि ये भी एकान्तर कोण हैं)
अब, कोण BAC, सरल रेखा FG पर तीसरा कोण है। आपको अपने स्कूल के दिनों से याद होगा कि किसी सरल रेखा पर (एक बिन्दु पर बने) सारे कोणों का योग 180 डिग्री होता है। इसे ऋजु कोण कहते हैं और यह 360 डिग्री के सम्पूर्ण कोण का आधा होता है। अर्थात, कोण GAC + कोण BAC +  कोण FAB = 180 डिग्री।
लेकिन कोण GAC = कोण ACB (जो त्रिभुज के तीन में से एक कोण है) और कोण FAB = कोण ABC (यह भी त्रिभुज के तीन कोणों में से एक है), जैसा कि हम पहले ही देख चुके हैं। तीसरा कोण BAC (‘a’ के रूप में चिन्हित) ऋजु कोण और ∆ABC में उभयनिष्ठ (कॉमन) है। अत: हम कह सकते हैं कि त्रिभुज ABC के तीन कोणों का योग 180 डिग्री है।
अपना तर्क पूरा करने के बाद चन्ना ने फौरन जोड़ा, “QED!” और इन्तज़ार करने लगे कि हम इसे पचा लें।

प्रमाण बेढंगे हो सकते हैं, सुरुचिपूर्ण हो सकते हैं, सुन्दर हो सकते हैं, चौंकाने वाले हो सकते हैं...। गणितज्ञ तार्किक प्रक्रिया के बारे में अपने एहसासों को ऐसे ही विशेषणों से व्यक्त करते हैं। मैं कोई गणितज्ञ नहीं हूँ लेकिन मुझे भी लगता है कि यह अत्यन्त प्रारम्भिक प्रमाण सुरुचिपूर्ण है। यह थोड़ा हतोत्साहित भी कर सकता है क्योंकि इस तरह के तर्क के अभ्यस्त होने में समय लगता है। लेकिन यह गणित का मर्म है, बात चाहे ज्यामिति की हो, बीजगणित की हो या किसी अन्य शाखा की।

प्रमेय साबित करने में स्वयंसिद्ध की भूमिका
आप शायद पूछेंगे, “यह तो ठीक है, पर इसमें हो क्या रहा है?” हमने जिन भव्य स्वयंसिद्धों या अभिधारणाओं से शुरुआत की थी, उनसे इसका क्या लेना-देना है? तो चलिए उन पर लौटते हैं। हम वाकई देख सकते हैं कि उन स्वयंसिद्धों का उपयोग इस प्रमाण में कैसे किया गया है। दरअसल, समानान्तर अभिधारणा के बगैर हम सिद्ध नहीं कर सकते कि त्रिभुज के कोणों का योग 180 डिग्री होता है। जी, बिलकुल नहीं।
चलिए, मैं विरोधी वकील बनकर चन्ना के साथ काल्पनिक बातचीत करता हूँ। मैं चन्ना के पास जाकर कहता हूँ, “जनाब, मुझे ये अभिधारणाएँ/स्वयंसिद्ध मान्यताएँ पसन्द नहीं हैं, ये इतनी भ्रामक हैं।”
आदत के मुताबिक, वे मुस्करा दिए। लेकिन उनके चेहरे पर एक सवालिया भाव है। “क्या बात है, रा?” ‘रा’ किसी लड़के को स्नेहपूर्वक सम्बोधित करने के लिए एक तेलुगु शब्द है। चन्ना इसका उपयोग कई बार किया करते थे।

मैं अपनी बात आगे बढ़ाता हूँ, “बात को आगे बढ़ाने के लिए मान लीजिए, हम कुछ अभिधारणाओं को तिलांजलि दे देते हैं। तब भी क्या ‘त्रिभुज प्रमेय’ का पुख्ता प्रमाण हासिल करना सम्भव होगा, जैसा कि हमने अभी किया है? मुझे (अभिधारणाओं की अनिवार्यता की) इस बात को स्वयंसिद्ध और सवालों से परे मानने में दिक्कत है।”
मुझे याद है, स्वयंसिद्ध मान्यताओं का यह गोरखधन्धा मुझे परेशान करने लगा था।
चन्ना तुरन्त देख लेते हैं कि मैं किस उधेड़बुन में हूँ। वे जानते हैं इससे कैसे निपटना है। “ठीक है,” वे कहते हैं, “हम अभिधारणा क्रमांक 1 व 2 को हटा देते हैं क्योंकि तुम्हें ये वैसे भी पसन्द नहीं हैं। तब क्या होगा?”
“यदि तुम अभिधारणा 1 को हटा दोगे तो तुम किसी बिन्दु को किसी अन्य बिन्दु से एक सरल रेखा की मदद से नहीं जोड़ पाओगे। अभिधारणा 1 हमें यह बुनियाद उपलब्ध कराती है। इसी प्रकार से यदि तुम अभिधारणा 2 को हटा दोगे तो तुम त्रिभुज ABC की भुजा BC को आगे नहीं बढ़ा पाओगे, जैसा कि हमने किया था। समझे?”
फिर मैं सोचता हूँ कि यदि हम अभिधारणा 5 (समानान्तर मान्यता) को हटा देते हैं तो हम दो समानान्तर रेखाओं को एक तिर्यक रेखा द्वारा काटे जाने पर एकान्तर कोणों के बराबर होने की बात का उपयोग भी नहीं कर पाएँगे। यानी, इस बात का पुख्ता प्रमाण हासिल करना असम्भव हो जाएगा कि त्रिभुज के तीन कोणों का योग 180 डिग्री होता है।
तो बात साफ है। हम इन अभिधारणाओं यानी स्वयंसिद्ध मान्यताओं के बगैर नहीं रह सकते। मैं सोचता हूँ, विचारों की कोई भी तार्किक व्यवस्था विकसित करने के लिए हमें कुछ मान्यताओं की ज़रूरत होती ही है। स्कूल में हमने युक्लिड की जो ज्यामिति पढ़ी थी, वह ऐसी ही एक व्यवस्था है।

यूक्लिड की भूमिका और महत्व
थोड़े और पेचीदा स्तर पर, युक्लिड की अवधारणाएँ हमें उस जगह (space) के बारे में कुछ बता सकती हैं जिसमें हम रहते हैं। जब मैं जगह कहता हूँ, तो मेरा आशय हमारे जीवन के भौतिक यथार्थ से है। हम इसे मानकर चलते हैं और इसके बारे में ज़्यादा सवाल-जवाब नहीं करते - जैसे, इसकी संरचना। मुझे चन्ना के साथ हुई यह चर्चा स्पष्ट रूप से याद है। कुछ बहस भी हुई थी। जैसे, यदि हम रेखा को दोनों दिशाओं में आगे बढ़ाने सम्बन्धी द्वितीय अभिधारणा को लें, तो हम इस विचार पर पहुँचते हैं कि जगह ‘असीम’ है। कौन जानता है कि ऐसा ही है? इस बात को लेकर अन्तहीन बहस हो सकती है कि क्या कोई रेखा लगातार बढ़ती ही जा सकती है। फिर, अभिधारणा 5 को लेकर विवाद है। उसकी बात मैं जल्दी ही करूँगा।
हमने यहाँ जो उदाहरण लिया, वह ज्यामिति का है। और इसने मुझे यह स्वीकार करने को विवश कर दिया कि त्रिभुज प्रमेय या गणित में किसी भी अन्य प्रमेय को सिद्ध करना शुरू करने से पहले अभिधारणा महत्वपूर्ण ही नहीं बल्कि अनिवार्य हैं। युक्लिड की बुद्धिमत्ता शायद स्पष्ट निरूपण में है। गणित के इतिहासकार प्राय: बताते हैं कि युक्लिड के निष्कर्ष विभिन्न संस्कृतियों में पूर्ववर्ती गणितज्ञों द्वारा प्रस्तुत किए गए थे क्योंकि ज्यामिति का विकास तो विभिन्न समाजों में मापन की ज़रूरत के चलते हुआ था। लेकिन वे कहते हैं कि युक्लिड वे पहले व्यक्ति थे जिन्होंने तार्किक निगमन के लिए एक समग्र प्रणाली अथवा नियमों का विकास किया था। ये नियम ठोस उदाहरणों से अमूर्त अवधारणाओं की ओर संक्रमण (ट्रांज़िशन) के द्योतक हैं। यह वह तरीका है जिस पर आजकल की हाई स्कूल गणित शिक्षा टिकी है।

मैं यह दोहरा रहा हूँ क्योंकि चन्ना ने यह दिलचस्प इतिहास हमारे साथ साझा किया था। कल्पना कीजिए - हम ऐसा कुछ सीख रहे थे जिसे दो सहस्त्राब्दि पहले सोचा गया था और एक किताब में लिख दिया गया था। हम सोच भी नहीं सकते थे कि गणित ऐसा भी हो सकता है। आने वाले महीनों और वर्षों में हम ज्यामिति, बीजगणित, त्रिकोणमिति और बीजगणितीय ज्यामिति में कई प्रमेयों को सिद्ध करने वाले थे। यह सब हाई स्कूल के हर गणित छात्र की नियमित खुराक का हिस्सा है।
इसमें से कुछ भी हमारी पाठ्य पुस्तक का हिस्सा नहीं था। चन्ना के लिए इसे छूना ज़रूरी नहीं था। लेकिन उन्होंने किया, यह मानकर कि हम सब यह कहानी सुनने के हकदार हैं। इसीलिए तो उन्होंने हमें यह सुनाने की ज़हमत उठाई। किसी भी अभिभावक या शिक्षक के लिए यह विश्वास ज़रूरी है - कि बच्चे के लिए विषय की गहरी समझ विकसित करना ज़रूरी है और वह कर सकता है। बदकिस्मती से, हम प्राय: बच्चों को कम करके आँकते हैं और उनकी सम्भावनाओं को नुकसान पहुँचाते हैं। हम उन्हें खारिज कर देते हैं और फिर जूझते हैं कि वे टेस्ट और परीक्षाओं से पार पा लें। हममें से कुछ तो अपने पूर्वाग्रहों को और भी आगे ले जाते हैं। हम मान लेते हैं कि कतिपय समुदायों से आने वाले कुछ बच्चे सीख ही नहीं सकते। कुछ शिक्षक यह भी मानते हैं कि लड़कियों की अपेक्षा लड़के बेहतर सीखते हैं। तब हम सारे बच्चों के साथ बराबरी का व्यवहार कैसे कर सकते हैं?

मुझे प्रमेय और उनके पेचीदा प्रमाणों का अध्ययन अच्छा लगता था, लेकिन कभी-कभार ही। मैं कामना करता रहता था कि इसकी बजाय चन्ना हमें ज़्यादा-से-ज़्यादा कहानियाँ सुनाएँ। कोई दिन ऐसा होता था कि किसी प्रमेय का प्रमाण आसानी-से मिल जाता था। खास तौर से मुझे याद है कि जब हम त्रिभुज के मध्य बिन्दु प्रमेय (Triangle Midpoint Theorem) पर चर्चा कर रहे थे, तब अचानक मुझे एक विचार कौंधा था। जब मैंने अपने प्रमाण के तर्क आत्मविश्वास से प्रस्तुत किए, तब चन्ना के चेहरे पर थोड़ा आश्चर्य का भाव था। वह पहली बार था कि मैंने तर्क की प्रक्रिया शुरू की थी। मैंने सशक्त महसूस किया।

किन्तु ऐसे दिन भी होते थे जब मुझे जूझना पड़ता था। अलबत्ता, चन्ना हमेशा की तरह जोश में आगे बढ़ते, ब्लैकबोर्ड को अन्तहीन प्रमेयों और दिमाग को चकरा देने वाले प्रमाणों से सजा देते और हर कदम पर हमसे सवाल पूछते जाते। हर प्रमाण पूरा करने के बाद वे QED लिखना कभी नहीं भूलते थे। हर प्रमेय के अन्त में QED लिखना एक रिवाज़ था जिसका पालन वे पूरी निष्ठा से करते थे।
कई वर्षों बाद, यह जानकर मुझे बहुत अच्छा लगा कि महात्मा गांधी युक्लिड की एलीमेंट्स में तर्क की ताकत के प्रशंसक थे। उन्हें यह पुस्तक स्कूल में पढ़ाई गई थी। अपनी आत्मकथा, सत्य के प्रयोग (The Story Of My Experiments With Truth), में वे याद करते हैं,

“जब प्रयत्न करते-करते मैं युक्लिड के तेरहवें प्रमेय पर पहुँचा, तो अचानक मुझे बोध हुआ कि भूमिति तो सरल-से-सरल विषय है जिसमें केवल बुद्धि का सीधा व सरल प्रयोग ही करना है, उसमें कठिनाई क्या है? उसके बाद तो भूमिति मेरे लिए सदा सरल और सरस विषय बना रहा।”
जो लोग स्कूल के शुरुआती वर्षों में युक्लिडियन ज्यामिति के साथ जूझते हैं, गांधी जैसे उनका हौसला बढ़ाते हुए कह रहे हैं: “तेरहवें प्रमेय का इन्तज़ार करो, मुझे यकीन है सब कुछ बदल जाएगा।”
चन्ना के साथ जो पहला प्रमेय हमने सिद्ध किया, उसने गणित की मेरी समझ को बदल डाला। इस अनुभव में कुछ तो अलग बात थी। इस दौरान चन्ना हमें हल्के-से धकेल रहे थे कि हम तथाकथित ‘भोले-भाले अनुभववाद’ (naÏve empiricism) से आगे बढ़ें। इस जुम्ले का मतलब होता है कि आप पैटर्न्स पर इस आधार पर विश्वास नहीं कर सकते कि कुछ संख्याओं को शामिल करके देख लिया कि वही परिणाम कुछ मामलों में मिलता है। जैसे हमने चन्ना से कहा था कि यदि चन्द त्रिभुजों के अन्त:कोणों का योग 180 डिग्री आता है, तो मान लेना चाहिए कि सारे त्रिभुजों के मामले में ऐसा ही होगा।

निसन्देह विज्ञान में इसी विधि का इस्तेमाल होता है, जहाँ आप वस्तुओं की यथार्थ दुनिया के साथ काम करते हैं। हम प्राकृतिक विश्व के अपने अवलोकनों के आधार पर प्रत्यक्ष मापन पर भरोसा करते हैं। इन अवलोकनों के आधार पर हम सामान्य सिद्धान्त बनाते हैं कि क्यों कोई चीज़ हो रही है। उसी तरह के और-और अवलोकन होने पर सिद्धान्त सुदृढ़ होता जाता है। फिर किसी समय यह एक नियम बन जाता है। लेकिन त्रिभुज वाले मामले में हम अटक गए क्योंकि हमें यह पता नहीं था कि प्रमेय की सत्यता स्थापित करने के लिए हमें कितने त्रिभुजों को नापना होगा। यही बात विकराल विपरीत उदाहरण के बारे में भी सही थी। फिर हमारा सामना युक्लिड से हुआ जिन्होंने हमें यह सिद्ध करने का रास्ता दिखाया कि चाहे जितने त्रिभुज नाप लें, यह प्रमेय खरी है। तो, गणितीय प्रमाण किसी दावे की सत्यता स्थापित करने के लिए अपरिहार्य औज़ार है।

बहुतेरी ज्यामितियाँ?
लेकिन कहानी में एक पेंच है। चलिए, मैं अब आता हूँ विवादास्पद समानान्तर मान्यता (अभिधारणा) पर। यह अभिधारणा हमें इस निष्कर्ष की ओर ले जाती है कि जगह सपाट है, वक्र नहीं है क्योंकि दो समानान्तर रेखाएँ अनिश्चित तौर पर आगे बढ़ती जा सकती हैं। युक्लिड के करीब 2000 वर्ष बाद ‘गैर-युक्लिडीय’ ज्यामिति के उद्भव के साथ इस मत को बदलना पड़ा था। मैं यहाँ इन ज्यामितियों को छू भर पाऊँगा। चन्ना ने भी इनकी संक्षिप्त चर्चा ही की थी।
याद कीजिए युक्लिड ने अभिधारणा 5 में क्या कहा था: यदि दो रेखाएँ किसी तीसरी रेखा को इस तरह काटें कि अन्त:कोणों का योग दो समकोण (180 डिग्री) से कम हो, यदि उन दो रेखाओं को अनिश्चित तौर तक उस दिशा में बढ़ाया जाए, जिस ओर कोण बने हैं, तो वे अनिवार्य रूप से एक-दूसरे को काटेंगी या मिल जाएँगी। इसे चित्र-3 में दर्शाया गया है, जहाँ अन्त:कोणों का योग a+b < 180 डिग्री है।

दूसरी ओर, युक्लिड के अनुसार, यदि अन्त:कोण a+b = 180 डिग्री है तो वे रेखाएँ, चाहे जितनी भी बढ़ाई जाएँ, कभी नहीं मिलेंगी।
अब चित्र-4 को देखिए। इसमें एक ऐसी स्थिति प्रस्तुत की गई है जो इस समझ को सिर के बल खड़ा कर देती है।
यह रेखाचित्र दर्शाता है कि अक्षांश और देशान्तर रेखाओं का ताना-बाना किस तरह बना है (अपनी भूगोल की कक्षा याद कीजिए और ग्लोब पर इस बात की जाँच कर लीजिए)। दो देशान्तर रेखाएँ (तीर के चिन्ह से दर्शाई गई हैं) अक्षांश रेखाओं (इन्हें भी तीर से दर्शाया गया है) को समकोण पर काटती हैं। अर्थात् समानान्तर अभिधारणा के हिसाब से दो देशान्तर रेखाएँ एक-दूसरे के समानान्तर हैं। अभिधारणा कहती है कि अनिश्चित दूरी तक बढ़ाए जाने पर इन रेखाओं को कभी नहीं मिलना चाहिए। मगर इस मामले में ये रेखाएँ ध्रुवों पर मिलती हैं, और पृथ्वी की सतह पर एक साफ-सुथरा त्रिभुज ABC बनाती हैं। तो यह एक ऐसे त्रिभुज का स्पष्ट उदाहरण है, जिसके तीन कोणों का योग (A+B+C) 180 डिग्री से अधिक है। इसके लिए एक अलग किस्म की ज्यामिति की दरकार है जिसमें युक्लिड का समानान्तर स्वयंसिद्ध सिद्धान्त काम ही नहीं करता।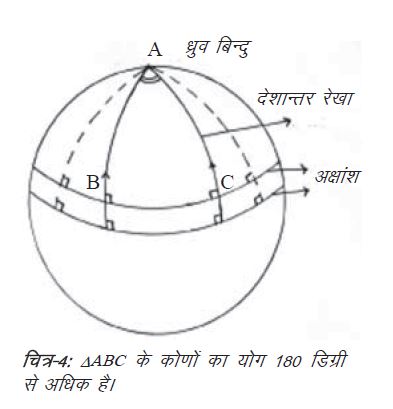

तो, युक्लिड पर्याप्त नहीं है। समझे? मामला कुछ और भी है। त्रिभुज सदैव सपाट सतहों पर ही तो नहीं बनाए जाते। हम गोलाईदार सतहों पर भी त्रिभुज बना सकते हैं। उक्त चित्र में एक और दिलचस्प बात यह देखी जा सकती है कि अक्षांश रेखाएँ भी एक-दूसरे के समानान्तर हैं। अलबत्ता, यदि हम पैदल या किसी वाहन में चढ़कर किसी अक्षांश रेखा पर यात्रा करें तो हम वास्तव में उसी बिन्दु पर लौट आएँगे जहाँ से यात्रा शुरू की थी। ऐसा होना युक्लिडियन जगह में सम्भव नहीं है जहाँ समानान्तर रेखाओं को दोनों दिशाओं मे अनिश्चित दूरी तक बढ़ाया जा सकता है।
हम बातचीत के इस सिलसिले को आगे बढ़ा सकते हैं। चित्र-5 में तीन त्रिभुजों को देखिए, जिन्हें तीन किस्म की सतहों पर बनाया गया है: एक सपाट सतह, जैसे आपकी मेज़ पर, जिसमें त्रिभुज के तीन कोणों का योग 180 डिग्री है (यही तो हमें स्कूल में बताया गया था); एक गोलीय सतह पर (जिसमें पृथ्वी की सतह के समान एक धनात्मक वक्रता है), जिसमें त्रिभुज के तीन कोणों का योग 180 डिग्री से ज़्यादा है; और एक अतिपरवलयाकार (hyperbolic) सतह पर (जिसकी वक्रता ऋणात्मक है, जैसे घोड़े की पीठ पर कसी ज़ीन) जहाँ तीन कोणों का योग 180 डिग्री से कम है। बाद वाली दो सतहों की ज्यामिति उस ज्यामिति से बहुत अलग होती है जो हमें स्कूल में सिखाई गई थी क्योंकि समानान्तर अभिधारणा यहाँ सत्य नहीं बैठती।

दो सबसे मशहूर गैर-युक्लिड ज्यामितियाँ हैं - ‘रीमैनियन’ और ‘लोबाचेव्सकियन’ ज्यामितियाँ।
मुझे कभी-कभी इस बात पर आश्चर्य होता है कि गणितज्ञों को गैर-युक्लिड ज्यामिति खोजने में इतना समय क्यों लगा, जबकि कलाकार और मूर्तिकार जैसे लोग तो गोलीय सतहों पर काम करते ही आए थे। फिर गोलीय दर्पण भी तो हैं। ऐसे क्षेत्रों में काम करने के लिए गोलीय सतहों के गुणधर्मों की काफी अच्छी समझ और हुनर की ज़रूरत होती है। खैर, इस मामले को यहीं छोड़ते हैं।
आप उपरोक्त तीन किस्म की सतहों को एक मिट्टी के घड़े (जाने-माने मटके) या फूलदान की मदद से भी समझ सकते हैं। इन पर आप तीनों किस्म के त्रिभुज बनाकर देख सकते हैं, यह इस बात पर निर्भर होगा कि आप त्रिभुज को मटके के किस हिस्से पर बनाते हैं। सोचिए इसके बारे में।

फिलहाल, प्रमाण के विचार की चर्चा पर लौटते हैं। यह लिखते-लिखते मुझे एक और चीज़ महत्वपूर्ण लग रही है। हाई स्कूल में प्रमाण के विचार के साथ जूझना थोड़ा भारी लग सकता है और कुछ लोग कह सकते हैं कि यह चीज़ 13-14 साल के बच्चों को नहीं पढ़ाई जानी चाहिए। लेकिन मुझे लगता है कि सामान्य तौर पर और गणित में प्रमाण और कुछ नहीं, सत्य की तलाश का ही दूसरा नाम है। यह निहित पैटर्न व अन्तरसम्बन्धों की व्यवस्थित खोज और उनके बारे में निष्कर्ष निकालने की प्रक्रिया है।

परम-सत्य विहीन, सत्य की तलाश
मेरे ख्याल में, सत्य की तलाश शिक्षा का प्रमुख कार्य है, और यह छात्र को परीक्षा उत्तीर्ण करने और बढ़िया अंक प्राप्त करने हेतु तैयार करवाने से कहीं आगे जाता है। सवाल यह है:
मैं कैसे जानता हूँ कि कोई बात सत्य है? और फिर, मैं यह कैसे जानता हूँ कि मैं जानता हूँ? यहीं पर यह ज़रूरी हो जाता है कि मैं उन तरीकों के प्रति आश्वस्त रहूँ जिनका उपयोग मैं किसी दावे को सत्य अथवा असत्य प्रमाणित करने के लिए कर रहा हूँ। मेरा मानना है कि सत्य की तलाश सिर्फ यह नहीं है कि आप सही ज्ञान अर्जित कर लें, बल्कि यह भी है कि आप उस सत्य को कर्म में जीएँ। निसन्देह, इसके लिए अलग से चर्चा की ज़रूरत होगी।
चन्ना से मुझे जो सन्देश मिला था, वह इसी तलाश को लेकर था। वे हमें सिर्फ यह नहीं कहते थे कि सवाल छुड़ाओ और आगे बढ़ जाओ। सावधानीपूर्वक चुने हुए पड़ावों पर वे परिप्रेक्ष्य साझा करते थे जो हमारी निर्धारित विषयवस्तु की माँग से कहीं आगे जाता था। उन्होंने ऐसे कई झरोखे खोल दिए जिनमें से हम कई विश्वों के अन्दर झाँक सकते थे, असीमित पैटर्न्स और अपने दिमाग की सम्भावनाओं को देख सकते थे।

मेरे विचार में परिप्रेक्ष्य का विकास सीखने का महत्वपूर्ण हिस्सा है। यह अच्छे अंक लाने से कहीं आगे जाता है। परिप्रेक्ष्य ही वह चीज़ होती है जो आपको किसी विषय से जुड़ने में और अन्तत: उसके प्रति प्रेम विकसित करने में मदद करता है। सीखने की प्रक्रिया में, परिप्रेक्ष्य विकसित करने का मतलब यह जानना होता है कि आप कोई चीज़ क्यों सीख रहे हैं। इसका सम्बन्ध यह जानने से भी है कि जो विचार या अवधारणा आप सीख रहे हैं, वह समय के साथ कैसे विकसित हुई है। और सबसे बड़ी बात तो यह समझना है कि आपने जो कुछ सीखा है, वह ज्ञान के अन्य खण्डों से और हमारे जीवन के अनगिनत पहलुओं से कैसे जुड़ा है। परिप्रेक्ष्य वह चीज़ है जो एक सीखने वाले के नाते हमें आज़ाद कर देता है और प्राय: हम ‘आहा!’ कह उठते हैं। यह आनन्द का सबब बनता है।
चन्ना ने जो कहानियाँ सुनाईं, उन्होंने मुझे परिप्रेक्ष्य विकसित करने में मदद की। उन्होंने मुझे यह समझने में समर्थ बनाया कि गणितीय विचारों को सीखने में मैं कहाँ स्थित हूँ। अब मैं समझता हूँ कि सत्य विभिन्न किस्म के हो सकते हैं, जो हमारे फ्रेम ऑफ रेफरेंस (निर्देश तंत्र) - यानी हम चीज़ों को कहाँ से देख रहे हैं - पर निर्भर करता है। हम यह बात युक्लिड के सन्दर्भ में देख ही चुके हैं; हालाँकि नए फ्रेम ऑफ रेफरेंस उभरने में लगभग 2000 साल लग गए थे। जिस चीज़ को युक्लिड की ज्यामिति में सत्य माना जाता है, वह अन्य किस्म की ज्यामिति में सत्य नहीं होती। ज्ञान अपने-आप में परम सत्य नहीं होता।
हम सचमुच चीज़ों की गहराई में घुस रहे थे।

शेषागिरी केएम राव: यूनीसेफ, छत्तीसगढ़ में शिक्षा विशेषज्ञ हैं। प्रारम्भिक शिक्षा और बाल्यावस्था में विकास में विशेष रुचि। साथ ही, आधुनिक शैक्षिक मुद्दों पर लिखने में दिलचस्पी।
अँग्रेज़ी से अनुवाद: सुशील जोशी: एकलव्य द्वारा संचालित स्रोत फीचर सेवा से जुड़े हैं। विज्ञान शिक्षण व लेखन में गहरी रुचि।
यह लेख एकलव्य द्वारा प्रकाशित पुस्तक द जेंटलमैन हू टॉट इंफिनिटी से लिया गया एक अंश है।