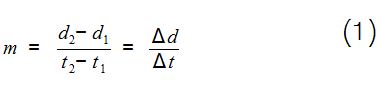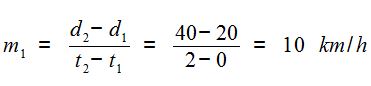विवेक मेहता [Hindi,PDF 257 KB]
लाइनों का नामकरण - लेख में हमारी चर्चा का विषय थीं लाइनें - सीधी सपाट लाइनें। उस लेख में हमने लाइनों को एक-दूसरे से अलग-अलग पहचानने के ग्राफ-आधारित एक तरीके पर बात की थी। साथ ही यह भी देखा था कि एक ग्राफ पर दो अक्षों के सापेक्ष खींची गई एक लाइन का इस्तेमाल हम उन दो अक्षों को दर्शाती राशियों के बीच के सरल-रेखीय सम्बन्ध को दर्शाने के लिए भी करते हैं।
इस लेख में हम गति से जुड़े ग्राफ व उनमें खींची लाइनों पर बात करेंगे। हम देखेंगे कि ये लाइनें क्या दर्शाती हैं और क्या नहीं, और कोशिश करेंगे गति के समीकरणों को इन लाइनों के ज़रिए समझने की।
दूरी-समय ग्राफ
तो आइए शुरुआत करते हैं - एक दूरी-समय ग्राफ व उसमें खींची दो लाइनों से (चित्र-1) और देखते हैं कि इस ग्राफ से हम क्या जान सकते हैं। सबसे पहले हम देखते हैं कि दूरी-समय ग्राफ के मामले में हमने अक्ष-y पर दूरी व अक्ष- x पर समय को दर्शाया है। समय को घण्टों व दूरी को किलोमीटर में लिया गया है।1
अगली बात जो इस ग्राफ में दिखाई देती है वो यह कि इसमें लाइन L1 व L2 के माध्यम से दो अलग-अलग गतियों को दर्शाया गया है। अब ये गतियाँ एक ही वस्तु की दो अलग-अलग दिनों की गति है (जैसे किसी धावक के दो अलग-अलग दिनों की प्रैक्टिस का रिकॉर्ड या एक ही बस की दो अलग-अलग दिनों की गति) या दो अलग-अलग वस्तुओं की एक ही समय पर गतियाँ (जैसे कि दो धावकों की एक दौड़ प्रतियोगिता, या एक ही समय पर दो बसों का बस-स्टाप से छूटना), इसके बारे में अकेले ग्राफ को देखकर तो कुछ भी पता नहीं चलता। एक और बात जो इस ग्राफ से हमें नहीं पता चलती है वो यह कि ये गतियाँ किस दिशा में या किस पथ पर हुई हैं। उदाहरण के तौर पर अगर हम यह मान लें कि यह ग्राफ दो धावकों की एक मैराथॉन दौड़ से जुड़ा हुआ है तो इस ग्राफ को देखकर हम यह नहीं बता सकते कि धावक किसी स्टेडियम के अन्दर ही गोल-गोल चक्कर लगा रहे थे या फिर खुली सड़क पर दौड़ रहे थे।
यह तो रही बात कि यह ग्राफ हमें क्या नहीं बतलाता। अब ज़रा देख लें कि यह ग्राफ हमें बतलाता क्या है। हम ग्राफ पर खींची हर एक लाइन के लिए Y-अन्त:-खण्ड व ढलान निकाल सकते हैं। Y-अन्त:-खण्ड का मान निकालने के लिए हमें यह देखना होता है कि लाइन अक्ष-Y को किस बिन्दु पर काट रही है। चित्र-1 के मामले में दोनों लाइनें दूरी के अक्ष को एक ही बिन्दु (0, 20) पर काट रही हैं, इसलिए इन दोनों के लिए y-अन्त:-खण्ड का मान होगा c1 = c2 = 20। इसी तरह ढलान निकालने के लिए हमें बारी-बारी से दोनों लाइनों पर कोई भी दो बिन्दु (t1, d1) व (t2, d2) लेने होंगे और समीकरण 1 में दिखलाया गया अनुपात निकालना होगा:
अगर लाइन L1 के लिए हम दो बिन्दु (0, 20) व (2, 40) लें तो ढलान मिलेगी:
इसी तरह लाइन L2 के लिए मिलने वाली ढलान होगी m2 = 5 km/h.
एक जायज़ सवाल उठता है कि दूरी-समय ग्राफ की लाइनों की ढलान ‘m’ व अन्त:-खण्ड ‘c’ किन भौतिक राशियों को दर्शाते हैं। आइए देखते हैं।
c व m के मायने
क्या हैं दूरी-समय ग्राफ में लाइनों के y-अन्त:-खण्ड व ढलान के मायने?
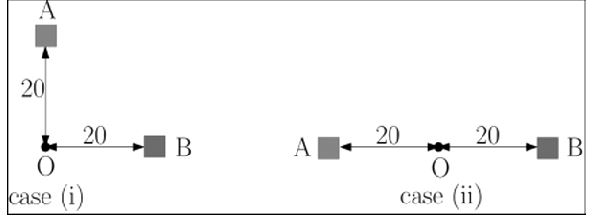
ध्यान दीजिए कि y-अन्त:-खण्ड हमने उस बिन्दु के सापेक्ष लिया है जिसके लिए समय का मान शून्य है। समय के शून्य होने का मतलब उस क्षण से हुआ जिस पर हमने वस्तु की गति का अध्ययन शुरूकिया। यह बतलाता है कि उस क्षण पर सन्दर्भ बिन्दु के सापेक्ष वस्तु की स्थिति क्या थी या वस्तु कितनी दूरी तय कर चुकी थी।3 चित्र-1 में दर्शाए गए दूरी-समय ग्राफ के सन्दर्भ में हम कह सकते हैं कि जब हमने उन वस्तुओं का अध्ययन शुरु किया जिन्हें लाइन L1 व L2 से दर्शाया गया है, उस क्षण पर दोनों ही वस्तुएँ सन्दर्भ बिन्दु से 20 km की दूरी पर थीं या दोनों ही वस्तुएँ उस क्षण तक सन्दर्भ बिन्दु से 20 km की दूरी तय कर चुकी थीं। इस बिन्दु पर कुछ देर ठहरकर ज़रा यह सोचिए कि क्या हम दोनों वस्तुओं की एक-दूसरे के सापेक्ष दूरी के बारे में कुछ कह सकते हैं? इस सवाल का जवाब होगा - नहीं। चित्र-2 में ऐसी दो स्थितियाँ दिखलाई गई हैं जिनमें वस्तुओं की सन्दर्भ बिन्दु से दूरी एक बराबर होने के बावजूद, वस्तुओं के बीच की दूरी अलग-अलग होगी। ज़ाहिर तौर पर ऐसी अनगिनत स्थितियाँ हो सकती हैं। क्या आप इस तर्क से सहमत हैं?
अब आते हैं ढलान पर। पिछले लेख में हमने देखा था कि एक ग्राफ पर खींची किसी लाइन की ढलान एक नियत राशि होती है व अक्ष-x की राशि के साथ अक्ष-y की राशि में होने वाले परिवर्तन की दर को दर्शाती है। इस तरह देखें तो एक दूरी-समय ग्राफ में एक लाइन की ढलान समय के साथ-साथ वस्तु के द्वारा तय की गई दूरी की दर को दर्शाएगी। आम बोलचाल की भाषा में इस दर को ही किसी वस्तु की स्पीड, रफ्तार या चाल कहते हैं। दूरी-समय ग्राफ पर किसी लाइन की ढलान जितनी ज़्यादा होगी, वस्तु की रफ्तार उतनी ही तेज़ होगी। समीकरण (1) से हम देख सकते हैं कि इस दर की इकाई होगी दूरी प्रति इकाई समय। अगर दूरी किलोमीटर व समय घण्टों में लिया जाए तो स्पीड की इकाई होगी किलोमीटर प्रति घण्टा। चित्र-1 के मामले में लाइन L1 के द्वारा दर्शाई गई वस्तु की चाल है 10 कि.मी. प्रति घण्टा (km/h) व लाइन L2 के लिए 5 कि.मी. प्रति घण्टा। क्यूँकि वस्तु की चाल समय के साथ नहीं बदल रही इसलिए इसे एकरूप चाल (constant speed) कहते हैं (देखें बॉक्स-1)।
आम तौर पर हम जब किसी वस्तु की रफ्तार की बात करते हैं तो सिर्फ उसके मान की ही बात करते हैं जैसे कि फलाँ गाड़ी 60 कि.मी. प्रति घण्टा की रफ्तार से चल रही है। लेकिन हमेशा बस इतना ही बता देना तो काफी नहीं होता। अक्सर ही वस्तु की चाल के साथ-साथ उसकी चाल की दिशा भी बतलाना ज़रूरी होता है - वरना दाँतों के साथ-साथ हड्डियाँ भी टूट सकती हैं।
स्पीड बनाम वेग
जब स्पीड या चाल की जानकारी वस्तु के बढ़ने की दिशा के साथ दी जाती है तो विज्ञान की भाषा में उसे वस्तु का वेग (velocity) कहते हैं। वेग की इकाई भी स्पीड या चाल की इकाई ही होती है। अगर कोई वस्तु एकरूप चाल से एक सीधी दिशा में बढ़ रही हो तो हम कह सकते हैं कि वस्तु एकरूप वेग (constant velocity) से गति कर रही है। एकरूप वेग की गति के मामले में न ही वस्तु की चाल में कोई परिवर्तन आता है और न ही उसकी चाल की दिशा में। हमने पहले ही देखा एक दूरी-समय ग्राफ की लाइन की ढलान हमें स्पीड यानी कि चाल का मान बतलाती है। यह चाल किस दिशा में है, इसकी जानकारी दूरी-समय ग्राफ से नहीं मिलती।
तय दूरी बनाम सन्दर्भ से दूरी
तो कुल मिलाकर हमें चित्र-1 के ग्राफ से जानकारी मिलती है कि लाइन L1 से जुड़ी वस्तु शुरुआत में सन्दर्भ बिन्दु से 20 कि.मी. की दूरी पर थी या 20 कि.मी. की दूरी तय कर चुकी थी, जहाँ से अगले 6 घण्टों में उसने 10 किमी/घण्टा की एकरूप चाल से 60 कि.मी. की दूरी तय की। वहीं लाइन L2 से जुड़ी वस्तु शुरुआत में सन्दर्भ बिन्दु से 20 कि.मी. की दूरी पर थी, जहाँ से अगले 8 घण्टों में उसने 5 कि.मी./घण्टा की एकरूप चाल से 40 कि.मी. की दूरी तय की।
लाइन L1 के लिए ग्राफ से मिली जानकारी के आधार पर क्या हम यह बतला सकते हैं कि 6 घण्टों के बाद वस्तु सन्दर्भ बिन्दु से कितनी दूरी पर होगी? इसका जवाब भी नकारात्मक ही होगा। ऐसा इसलिए क्यूँकि हमें यह तो पता है कि वस्तु 6 घण्टों में 10 किमी/घण्टा की एकरूप चाल से 60 कि.मी. की दूरी तय करती है लेकिन यह दूरी किस दिशा या कैसे पथ पर तय की गई है इसकी जानकारी हमें मात्र ग्राफ से नहीं मिलती।
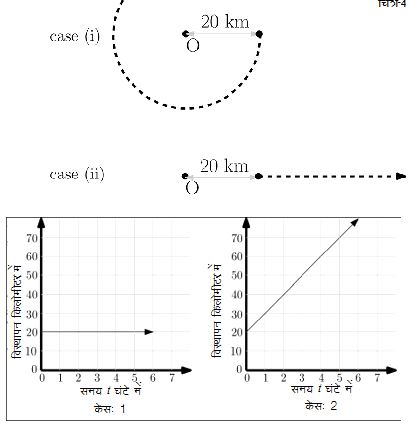
चित्र-4 में वस्तु के लिए सम्भावित अनगिनत पथों में से दो पथ दर्शाए गए हैं। इन दोनों मामलों में चाल व सन्दर्भ बिन्दु O से शुरुआती दूरी समान होने के बावजूद अन्त में सन्दर्भ बिन्दु से वस्तु की दूरी अलग-अलग होगी। पहले मामले में वस्तु एक वृत्तीय पथ पर चल रही है, जिसके चलते सन्दर्भ बिन्दु ग्र् से उसकी दूरी हमेशा ही 20 कि.मी. होगी। गौर करने वाली बात है कि इस मामले में वस्तु के आगे बढ़ने की दिशा लगातार बदलेगी, जिसके चलते एकरूप चाल होने के बाद भी यह एकरूप वेग की गति नहीं है। दूसरे मामले में वस्तु सन्दर्भ बिन्दु व शुरुआती बिन्दु को जोड़ने वाली रेखा पर सन्दर्भ बिन्दु के विपरीत दिशा में चल रही है जिसके चलते अन्त में वस्तु की सन्दर्भ बिन्दु से दूरी होगी 80 कि.मी.। इस मामले में चूँकि वस्तु के बढ़ने की दिशा बदल नहीं रही व चाल एकरूप है, इसलिए ये मामला एकरूप वेग की गति का है। इन दोनों मामलों में एक बराबर दूरी तय करने के बावजूद वस्तु की सन्दर्भ बिन्दु से दूरी अलग-अलग होगी। हम देख सकते हैं गतिमान वस्तु के लिए दूरी से जुड़ी दो विभिन्न भौतिक राशियाँ होती हैं - (1) वस्तु के द्वारा तय की गई दूरी व (2) सन्दर्भ बिन्दु से वस्तु की न्यूनतम4 दूरी। इस न्यूनतम दूरी के लिए एक खास शब्द का इस्तेमाल किया जाता है - विस्थापन (displacement)। वेग की ही तरह विस्थापन भी एक सदिश राशि है यानी कि मान के साथ इसमें दिशा की भी जानकारी होती है। चित्र-4 में दिखलाए गए दोनों मामलों के लिए वस्तु के द्वारा तय की गई दूरी व समय के बीच का ग्राफ तो एक ही होगा लेकिन विस्थापन के मान व समय के बीच के ग्राफ अलग-अलग (देखें चित्र-4)। इसलिए किसी वस्तु के लिये दूरी-समय ग्राफ बनाते हुए ये साफ-साफ बतलाना ज़रूरी होगा कि दूरी के अक्ष पर कौन-सी माप ली गई है वरना चित्र-4 केस (i) को देखकर कोई इस गलत निष्कर्ष पर भी पहुँच सकता है कि वस्तु स्थिर है। जबकि इस मामले में वस्तु एक वृत्तीय पथ पर एकरूप चाल से गतिमान है। गौर कीजिए कि चित्र-4 में अक्ष-y पर विस्थापन के मान को दर्शाया गया है विस्थापन को नहीं। ऐसा इसलिए क्यूँकि एक आम गति के लिए ग्राफ पर विस्थापन की दिशा दर्शा पाना सम्भव नहीं। यही बात वेग पर भी लागू होती है। लेकिन एक खास तरह की गति के लिए हम वेग व विस्थापन को भी ग्राफ पर दर्शा सकते हैं।
सरल-रेखीय गति
यह खास गति उस परिस्थिति से जुड़ी हुई है जिसमें वस्तु एक सीधी रेखा या पथ पर गतिशील हो, एक सरल-रेखीय गति, यानी कि चलते हुए वस्तु की दिशा में कोई परिवर्तन न हो। ऐसे पथ पर अगर वस्तु एकरूप चाल से चल रही हो तो यह गति एकरूप वेग की गति होगी। गणनाओं की आसानी के लिए हम यह मान लेते हैं कि सन्दर्भ बिन्दु भी इसी पथ पर है (चित्र-5 (a))।
इस पथ पर पहले वस्तु की स्थिति की बात कर लेते हैं। सन्दर्भ बिन्दु के सापेक्ष वस्तु की स्थिति या तो दाहिनी ओर हो सकती है या बाईं ओर (चित्र-5 (b)। वस्तु की स्थिति स्पष्ट तरीके से बतलाने के लिए हमें न केवल यह बतलाना होगा कि वस्तु की सन्दर्भ बिन्दु से दूरी कितनी है बल्कि यह भी कि वस्तु किस ओर है। ऐसे में चित्र-2 केस (ii) की वस्तुओं की स्थिति हम कुछ इस तरह से बतलाएँगे - वस्तु A की सन्दर्भ बिन्दु से दूरी = 20 km बाईं ओर व वस्तु ए की सन्दर्भ बिन्दु से दूरी =20 km दाईं ओर। इस बात को कम शब्दों में कहने का एक और तरीका भी है। अगर हम सन्दर्भ बिन्दु के बाईं ओर की दूरियों को ऋणात्मक व दाईं ओर की दूरियों को धनात्मक मान लें तो हम कह सकते हैं कि वस्तु B की सन्दर्भ बिन्दु से दूरी = +20km व वस्तु ए की सन्दर्भ बिन्दु से दूरी = -20 km। इस तरह ऋणात्मक व धनात्मक चिन्हों के साथ दूरी को अभिव्यक्त कर हम न केवल यह जान सकते हैं कि वस्तु सन्दर्भ बिन्दु से कितनी दूरी पर है बल्कि यह भी कि वो किस ओर है। एक दूरी-समय ग्राफ के दूरी के अक्ष पर शून्य के ऊपर धनात्मक व नीचे की ओर ऋणात्मक दूरियों को दर्शाकर हम यह व्यवस्था ग्राफ पर भी बना सकते हैं। दूसरे शब्दों में कहें तो सरल-रेखीय गति के मामले में हम एक ग्राफ पर विस्थापन को दर्शा सकते हैं जो कि एक आम गति के मामले में सम्भव नहीं था।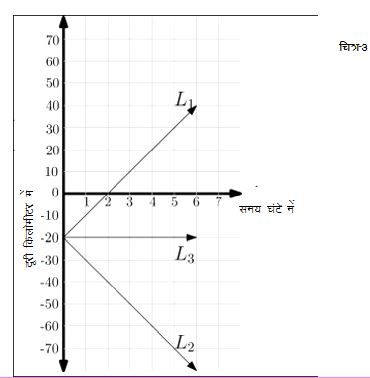
इसी तरह चाल की दिशा के लिए भी हम एक व्यवस्था बना सकते हैं। अगर किसी भी शुरुआती स्थिति से वस्तु की बाईं ओर चलने पर चाल को ऋणात्मक व दाईं ओर चलने पर धनात्मक मान सकते हैं (चित्र-5 (c))। अगर वस्तु अपनी शुरुआती स्थिति से 10km/h की एकरूप चाल से बाईं ओर चले तो हम कहेंगे कि वस्तु का एकरूप वेग है -10 km/h, वहीं अगर वस्तु दाईं ओर बढ़े तो हम कहेंगे वस्तु का एकरूप वेग है +10 km/h। गुणात्मक तौर पर देखें तो किसी सन्दर्भ बिन्दु के सापेक्ष एक सरल-रेखीय गति की इस व्यवस्था में एकरूप चाल के तीन मामले हो सकते हैं।
ऐसे मामले जिनमें वस्तु की एकरूप चाल धनात्मक हो यानी कि वस्तु पथ पर दाईं ओर एकरूप चाल से बढ़ती जाए। अगर वस्तु का शुरुआती विस्थापन ऋणात्मक हो तो पहले-पहल सन्दर्भ बिन्दु व वस्तु के बीच की दूरी घटेगी। एक क्षण ऐसा आएगा जब वस्तु सन्दर्भ बिन्दु पर ही होगी व उसके बाद वस्तु की सन्दर्भ बिन्दु से दूरी धनात्मक दिशा में एकसमान दर से लगातार बढ़ती जाएगी।
ऐसे मामले जिनमें वस्तु की एकरूप चाल ऋणात्मक हो यानी कि वस्तु पथ पर बाईं ओर एकरूप चाल से बढ़ती जाए। अगर वस्तु का शुरुआती विस्थापन ऋणात्मक हो तो वस्तु की सन्दर्भ बिन्दु से दूरी ऋणात्मक दिशा में एकसमान दर से लगातार बढ़ती जाएगी।
एक तीसरा मामला और बनता है जिसमें वस्तु अपनी जगह पर ही बनी रहे। ऐसे मामलों में वस्तु की एकरूप चाल शून्य होगी। चित्र-6 में क्या आप इन तीनों मामलों को पहचान सकते हैं?
ये तीनों मामले एक विस्थापन-समय ग्राफ पर कैसे दर्शाए जाएँगे? कोशिश कीजिए दर्शाने की।
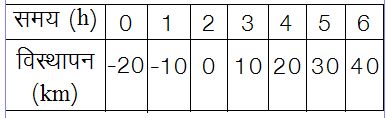
एक खास स्थिति को लेते हैं जिसमें वस्तु का शुरुआती विस्थापन -20 km व एकरूप वेग 10 km/h हो। यह गति पहले मामले के अन्तर्गत आएगी। चूँकि वस्तु का शुरुआती विस्थापन ऋणात्मक व एकरूप वेग धनात्मक है तो पहले वस्तु सन्दर्भ बिन्दु की ओर बढ़ेगी। अगले दो घण्टों में वस्तु 10 km/hकी दर से 20 कि.मी. की दूरी तय कर सन्दर्भ बिन्दु पर पहुँच जाएगी जिसके बाद वस्तु धनात्मक दिशा में सन्दर्भ बिन्दु से लगातार दूर जाती जाएगी। अगर 6 घण्टों के लिए वस्तु के विस्थापन के लिए एक तालिका बनाएँ तो कुछ ऐसी संख्याएँ मिलेंगी:
क्या आप समय और विस्थापन के बीच कोई सम्बन्ध देख पा रहे हैं?
‘लाइनों का नामकरण’ लेख में हमने देखा था कि किसी ग्राफ में खींची लाइनें ग्राफ के अक्षों को दर्शाती चर-राशियों x व y के बीच सम्बन्ध को दर्शाती हैं। इस सरल रेखीय सम्बन्ध को लाइन की ढलान ‘m’ व y अन्त:-खण्ड ‘c’ के लिए समीकरण (2) से दर्शा सकते हैं:
y = mx + c ------------------ (2)
गौर कीजिए कि तालिका में दर्शाई गई गति के लिए अगर शुरुआती विस्थापन को d0, वेग को v, समय को t व tसमय बाद विस्थापन को d से दर्शाएँ तो इन राशियों के बीच सम्बन्ध होगा:
विस्थापन उ (एकरूप वेग न् समय) अ शुरुआती विस्थापन
d = vt + d0 ----------------- (3)
जोकि समीकरण (2) की तरह ही एक सरल-रेखीय सम्बन्ध है (चित्र-3, लाइन L1)। यहाँ यह बात दोहरा देना ज़रूरी है कि सम्बन्ध (3) सिर्फ और सिर्फ उन मामलों के लिए ही लागू होगा जिनमें वस्तु एकरूप वेग से गति कर रही हो यानी कि एकरूप चाल से एक सीधी रेखा या पथ पर गतिशील हो। चित्र-6 में अन्य दो मामलों को भी लाइन L2 व L3 से दर्शाया गया है। इन मामलों के लिए भी आप समीकरण (3) की वैधता जाँच सकते हैं।
इस भाग में बस इतना ही; अगले भाग में तैयार रहिए दर-दर भटकने के लिए। फिलहाल के लिए दो सवाल जो आप चाहें तो गति के ग्राफ की मदद से भी हल कर सकते हैं। देखिए तो ज़रा कि ग्राफ की मदद से इन्हें हल करने में कुछ आसानी होती है क्या?
* नदी के दो अलग-अलग छोरों पर खड़ी दो मोटरबोट एक ही समय पर दूसरे छोर की तरफ एकरूप वेग से चलना शुरु करती हैं, दूसरे छोर पर पहुँचकर बिना वक्त गवाए एकरूप वेग से ही वापिस पहले वाले छोर की तरफ आने लगती हैं। इनमें से एक बोट की एकरूप रफ्तार 10 m/s व दूसरे की 20 m/s है। अगर नदी की चौड़ाई 600 mहो तो बोट अपनी गति के दौरान किस-किस बिन्दु व समय पर एक-दूसरे का रास्ता काटेंगी?
* नदी के दो अलग-अलग छोरों पर खड़ी दो मोटरबोट एक ही समय पर दूसरे छोर की तरफ एकरूप वेग से चलना शुरु करती हैं। इस दौरान वे एक-दूसरे के रास्ते को पास वाले छोर से 400 m की दूरी पर काटती हैं। दूसरे छोर पर 10 मिनट रुककर एकरूप वेग से ही वापिस पहले वाले छोर की तरफ आने लगती हैं। इस रिटर्न यात्रा में वो फिर से एक-दूसरे के रास्ते को दूसरे छोर से 200 mकी दूरी पर काटती हैं। क्या आप बता सकते हैं नदी कितनी चौड़ी है?
(...जारी)
विवेक मेहता: आई.आई.टी., कानपुर से मेकेनिकल इंजीनियरिंग में पीएच.डी. की है। एकलव्य के विज्ञान शिक्षण कार्यक्रम के साथ फैलोशिप पर हैं जिसके तहत वे हाईस्कूल की कक्षाओं के लिए गतिविधि आधारित मॉड्यूल तैयार कर रहे हैं। यह प्रयास, कनेक्ट्ड लर्निंग इनिशिएटिव, टाटा सामाजिक विज्ञान संस्थान के समर्थन से संचालित है।
आभार: कनेक्ट्ड लर्निंग इनिशिएटिव टीम के सभी साथियों - राजेश, दीपक, भास, उमा व हिमांशु का, जिनके सुझावों के चलते यह लेख अपने वर्तमान रूप में आ पाया।