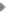लेखक: शैलेश ए. शिराली
अनुवाद: श्रीकान्त आप्टे [Hindi PDF, 137 kB]
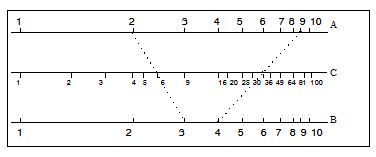
हम शुरू करेंगे उस पद्धति के वर्णन से जिसे कुछ लोग ‘इजिप्शियन गुणा’ के रूप में जानते हैं तो अन्य ‘रूसी गुणा’ के रूप में। स्पष्ट है कि इस पद्धति के कई दावेदार हैं! इस पद्धति को हम 11 x 17 की गणना कर समझाएँगे। नीचे बताए अनुसार दो पंक्तियाँ बनाइए; एक पंक्ति में अंक को क्रमिक रूप से आधा करिए (जैसे 11, 5, 2, 1; ध्यान दीजिए कि शेष राशि को नहीं लिया गया है) और दूसरी पंक्ति में क्रमिक रूप से दुगना करिए (जैसे 17, 34, 68, 136)।
इसी प्रकार, 47 x 91 की गणना के लिए हम आधे अंकों का एक क्रम (47, 23, 11, 5, 2, 1; पहले की भाँति शेष राशि को शामिल नहीं किया) और दुगने अंकों का एक क्रम (91, 182, 364, 728, 1456, 2912) बनाते हैं। पहले क्रम में एकमात्र सम अंक है 2, इसलिए हम 91 अ 182 अ 364 अ 728 अ 2912 की गणना करने पर पाते हैं 4277. इस प्रकार,
47 x 91 = 4277
कुछ अभ्यास
1. इस पद्धति का प्रयोग कर 23 x 43 और 231 x 311 की गणना करो।
2. 16 न् 103 की गणना में यदि 16 को आधा किया जाना है तो आधे किए जाने का क्रम बताओ।
3. यदि 64 x 103 की गणना में 64 को आधा किया जाना है तो क्या होगा?
4. इस पद्धति से दो अंकों की संख्याओं का गुणा करते समय हम पाते हैं कि हमें 7 से अधिक संख्याओं का जोड़ नहीं करना होता है। ऐसा क्यों है?
5. व्याख्या करो कि यह पद्धति उन उदाहरणों में कैसे काम करती है जिनमें आधी की जाने वाली संख्या 2 x 2 x 2...2 (अर्थात् दो के गुणनफल) के रूप में होती है।
6. व्याख्या करो कि यह पद्धति सामान्य रूप से कैसे काम करती है।
नैपियर की युक्ति
एक अन्य पद्धति ‘चौखाने’ की तकनीक है जिसका प्रारम्भ सम्भवत: भारत में दसवीं शताब्दी की शुरुआत में हुआ। इस तकनीक की जानकारी हम 47 x 91 की गणना के द्वारा देंगे। अलग-अलग अंकों के गुणनफल हैं 4 x 9 = 36, 7 x 9 = 63, 4 x 1 = 4 और 7 x 1 = 7. इन गुणनफलों को चित्र-1 में दर्शाए अनुसार क्रम में रखा जाता है।
बाएँ से दाएँ तिरछी रेखाओं को ऊपर से नीचे की ओर पढ़ें तो अंकों का योग होता है, 3, 12, 7 और 7. दाएँ से बाएँ चलते हैं तो हमें मिलता है गुणनफल 4277 (12 में 1 का अंक हासिल मानकर 3 में जोड़ दिया तो पाया 4)। इस तकनीक से वर्तमान में शालाओं में बड़ी संख्याओं के गुणा करने की तकनीक तक का विकास स्पष्ट हो जाता है।
कई शताब्दियों पश्चात् स्कॉटलैण्ड के जॉन नैपियर ने लकड़ी की छड़ों से एक उपकरण का पेटेंट कराया जो इन गणनाओं में मदद करता था। बाद में यही यंत्र ‘नैपियर बोन्स’ के नाम से जाना गया।
अभ्यास
1. वर्ग पद्धति का प्रयोग कर 1235 x 571 की गणना करो।
2. खुद के लिए नैपियर का यंत्र बनाओ और उसे बड़ी संख्या के गुणा हेतु प्रयोग करो।
गुणा सारणी
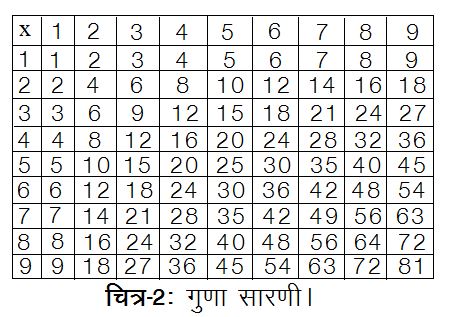
गुणा सारणियों जैसे 9 x 1 = 9, 9 x 2 = 18, 9 x3 =27...से सभी परिचित हैं। यद्यपि इस प्रकार की सारणियों की प्रमुख सीमा होती है कि वे पर्याप्त बड़ी नहीं होतीं। यदि कोई 1234 x 5678 की गणना करना चाहता है तो वह कैसे करे? क्या वह 1234 के गुणनफलों की सारणी (पहाड़ा) देखे? और 14259 x 71326 करना पड़े तो? ऐसी सारणी जो हर कल्पनीय गुणा कर सके, उसे लिखने के लिए दुनिया भर में पर्याप्त स्थान भी नहीं होगा। प्राचीन बैंकरों, खगोल-शास्त्रियों और नाविकों को रोज़मर्रा में इतनी बड़ी संख्याओं की हाथ से गणना का अनचाहा काम करना पड़ता था।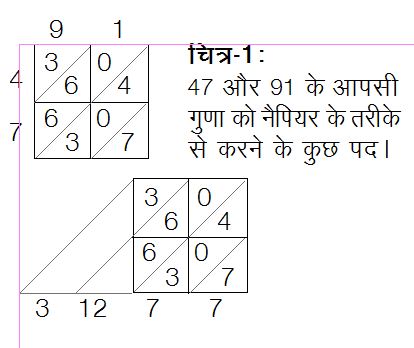
पढ़ने वाले की तत्काल समझ में आ जाता है कि यह तालिका कितनी बड़ी है और वो भी केवल 9 तक की संख्या के लिए। कठिनाई निस्सन्देह, इस क्रम के द्विआयामी होने से है; इसमें कुल 9 x 9 = 81 संख्याएँ हैं। इसके स्थान पर क्या एक आयामी क्रम तैयार करना सम्भव होगा?
बहुत पहले ही यह खोज लिया गया कि केवल वर्गों की सारणी तैयार कर लें तो यह सम्भव है। देखने योग्य मुख्य बात यह है कि a x b के गुणनफल को वर्गों के बाकी (जोड़-बाकी) के रूप में भी लिखा जा सकता है:
axb=[(a+b)/2]2 - [(a-b)/2]2
इस प्रकार हम 6 x14 की गणना नीचे बताए अनुसार करेंगे:
(14 + 6)/2 = 10,
(14 - 6)/2 = 4,
102 - 42= 100 - 16 = 84
तो उत्तर होगा 6 x 14 = 84
यह बड़ी संख्याओं के लिए भी कारगर है परन्तु इसके लिए हमारे पास वर्गों की विस्तृत सारणी होनी चाहिए। उदाहरणार्थ, 1357 x 9131 के लिए पहले हम गणना करेंगे,
(9131 - 1357)/2 = 3887
उसके बाद हम वर्गों की सारणी की मदद से पाते हैं,
52442 = 27499536,
38872 = 15108769
आखिर में हम घटाते हैं 27499536 - 15108769 = 12390767, इसलिए उत्तर होगा;
1357 x 9131 = 12390767
हमें उस बचत के महत्व को समझना चाहिए जो द्विआयामी क्रम की तुलना में एक आयामी क्रम तैयार करने से हासिल होती है (नोट करें कि विषम संख्याओं का गुणा सम संख्याओं से करने के लिए हमें सूची में आधे अंकों के वर्गों को भी शामिल करना होगा)।
उदाहरण
61 x72 के लिए हमें चाहिए,
66.52 = 4422.25 और
5.52 = 30.25; तब उत्तर मिलेगा,
4422.25 - 30.25 =4392
इससे गुणा तो हो जाएगा पर भाग देना हो तो हम क्या करेंगे, वर्ग और वर्गमूल की गणना कैसे होगी? स्पष्ट है कि इस पद्धति की उपयोगिता सीमित है।
अभ्यास
1. 211 x 319 और 171 x 352 की गणना इस पद्धति से करो।
2. तीन अंकों की संख्याओं का एक-दूसरे से गुणा करने के लिए वर्गों की कितनी बड़ी सारणी की आवश्यकता होगी? तीन अंकों के सभी सम्भव गुणनफलों को जानने के लिए हमें क्रम बनाना पड़े तो वह कितना बड़ा होगा?
अभाज्य संख्याओं के गुणनखण्ड 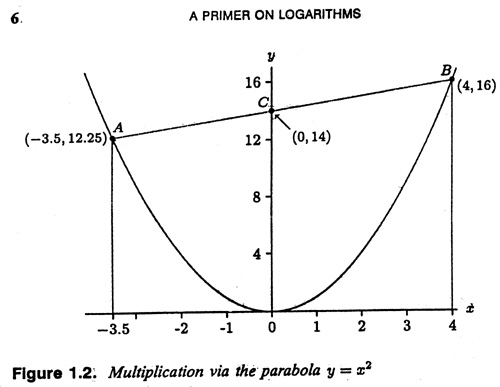 वर्गों की सारणी बनाने का अतिरिक्त लाभ यह मिलता है कि इससे अभाज्य संख्याओं के गुणनखण्ड (factorisation of prime numbers) जानने में हमें मदद मिलती है। तरीका बहुत आसान है; यदि संख्या ग़् को दो पूर्ण संख्याओं के वर्गों के अन्तर के रूप में लिखा जा सके, उदाहरण के लिए N = a2 - b2 जहाँ a - b एक से अधिक हो तब N = (a+b) (a-b) और हम पा जाते हैं वांछित गुणनखण्ड। इस पद्धति के प्रयोग की विधि हम यहाँ नीचे दे रहे हैं।
वर्गों की सारणी बनाने का अतिरिक्त लाभ यह मिलता है कि इससे अभाज्य संख्याओं के गुणनखण्ड (factorisation of prime numbers) जानने में हमें मदद मिलती है। तरीका बहुत आसान है; यदि संख्या ग़् को दो पूर्ण संख्याओं के वर्गों के अन्तर के रूप में लिखा जा सके, उदाहरण के लिए N = a2 - b2 जहाँ a - b एक से अधिक हो तब N = (a+b) (a-b) और हम पा जाते हैं वांछित गुणनखण्ड। इस पद्धति के प्रयोग की विधि हम यहाँ नीचे दे रहे हैं।
चित्र-3: पैराबोला, y= x2 के मार्फत गुणा करना।
मान लीजिए जिसका गुणनखण्ड जानना है, वह संख्या है N = 1073. हम संख्याओं की गणना प्रारम्भ करते हैं; N+12, N+22, N +32 और तब तक करते जाते हैं जब तक हमें वर्ग संख्या न मिल जाए। ज़ाहिर है कि इसके लिए हमें वर्गों की सारणी की आवश्यकता होगी। हम पाते हैं -
N+12 = 1074, N22 = 1077,
N+32 = 1082, N+42 = 1089 = 332
हम पाते हैं कि N+42 = 332 अर्थात् N = 332 - 42
= (33-4) (33+4) =29 x 37
इस प्रकार हमने ग़् के गुणकों को जान लिया।
मान लीजिए N= 2201. इस क्रम में पहली वर्ग संख्या होगी,
N+202 = 2201 + 400 = 2601 + 512
और इससे हमें मिलता है,
N = 512 - 202 = 31 x 71
अभ्यास
1. इस पद्धति से 2117 और 2911 के गुणक पता करो।
2. 64777 के गुणकों का पता लगाओ।
3. इस पद्धति की विशेषता बताओ। इसमें किन संख्याओं के गुणक जानने के लिए कम गणना करनी पड़ेगी और किन संख्याओं के लिए अधिक गणना करनी पड़ेगी?
पैराबोलिक गुणन
अब हम दो संख्याओं के गुणन की कम व्यावहारिक लेकिन एक रोचक पद्धति की चर्चा करेंगे।
इस पद्धति में एक वक्र रेखा ग्राफ बनाना होता है जिसे पैराबोला कहते हैं। इसके लिए सबसे पहले हम वर्ग संख्याओं की एक सारणी बनाते हैं, उसके पश्चात् हम ग्राफ पेपर पर निर्देशांक (x, x2) दर्शाते हुए कई सारे बिन्दु लगा देते हैं। (-4,16), (-3,9)......(1,1), ....(3,9), (4,16)... जैसा कि चित्र-3 में दर्शाया गया है। ये बिन्दु एक सुस्पष्ट वक्र रेखा बनाते हैं (ध्यान दीजिए दोनों अक्षों का पैमाना एक जैसा नहीं है। एक्स अक्ष की तुलना में वाई अक्ष का पैमाना ज़्यादा संघनित है)।
मान लीजिए हम दो संख्याओं 3.5 और 4 का गुणन करना चाहते हैं, (यद्यपि यह मामूली है पर उदाहरण के लिए चलेगा)। चित्र-3 के अनुसार एक्स अक्ष पर -3.5 और 4 से दो रेखाएँ खींचकर हमें पैराबोला पर बिन्दु A और B मिलते हैं (ध्यान दीजिए कि A बिन्दु के लिए हमने ऋणात्मक मान लिया है)। बिन्दु A और B को मिलाकर हमें AB रेखा मिलती है। यह रेखा x अक्ष के C बिन्दु पर मिलती है। क् से हमें मिलता है हमारा वांछित गुणनफल। चित्र में हम देखते हैं कि क् उ(0, 14)। इस प्रकार गुणनफल हुआ 14.
सामान्यतया a x b की गणना के लिए हम ॠ (-a, a2) और ए (b, b2) बिन्दुओं को मिलाते हैं तो Y रेखा पर बिन्दु C , जहाँ AB y रेखा को काटता है, से हमें चाहा हुआ गुणनफल प्राप्त हो जाता है।
कारण जानना आसान है। वक्र AB का ढलान है,
(b2 -a2) / b - (-a)
= (b2 - a2) / b+a = b-a
इस प्रकार यदि C = (0, c) हो तो BC और AB ढलानों को बराबर मानने पर हम पाते हैं,
(b2 - c) / c - 0 = b - a,
b2 - c = b(b - a),
c=ab
इस प्रकार y रेखा पर c का मान हुआ ab. यही उत्तर है।
नोमोग्राम पद्धति
ऊपर वर्णित ग्राफ पद्धति हमें नोमोग्राम की याद दिलाती है। यह ग्राफ पद्धति द्वि-परिवर्तनीय फंक्शन (two-variable function) f के विभिन्न मानों की गणना करने हेतु प्रयोग की जाती है (जैसा कि परिभाषा से ही स्पष्ट है, इसमें दो क्रियाओं की आवश्यकता होती है, उदाहरण के लिए f जोड़ भी हो सकता है और गुणा भी)। नोमोग्राम में आपके पास तीन समानान्तर पैमाने (मान या नाप) होते हैं जिनमें से प्रत्येक पर कुछ उपयुक्त तरीके की संख्याएँ लिखी रहती हैं। सुविधा के लिए हम ऊपर और नीचे के पैमानों को A और B नाम देंगे और बीच वाले पैमाने को C नाम देंगे। पैमानों पर मान किस तरह होंगे यह f के प्रकार पर निर्भर करेगा। प्रयोग की पद्धति इस प्रकार है: f(a, b) की गणना करने के लिए हम A और B पैमानों पर a और b की स्थिति का पता लगाते हैं; अब एक मापपट्टी/स्केल को इस प्रकार रखते हैं कि उसकी किनार a और b संख्याओं से होकर गुज़रे; तो C पैमाने पर जिस बिन्दु पर यह पैमाना मिलता है वहीं हमें हमारा उत्तर मिल जाता है। इंजीनियरिंग कारखानों में जहाँ खास प्रकार की गणनाएँ बार-बार करनी होती हैं वहाँ नोमोग्राम काफी उपयोगी होते हैं। इस पद्धति को अधिक अच्छे से समझने के लिए हम कुछ उदाहरणों पर विचार करेंगे।
* अंकगणितीय औसत (मध्यमान): मान लीजिए कि हमें f (a, b) = (a+b)/2 से माध्य फलन प्राप्त होता है। इस उदाहरण में तीनों पैमाने एक ही प्रकार से एक समान अंकित किए जाते हैं।
एक रेखा खींची गई है (चित्र-4) यह दर्शाने के लिए कि किस प्रकार 5 और 9 का गणितीय माध्य गणना द्वारा 7 होता है।
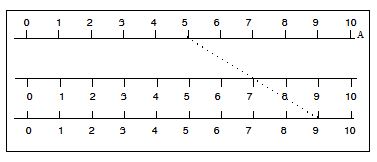
* गुणनफल: मान लीजिए कि f (a, b) = ab का गुणन फलन ढ है। इसके लिए उपयुक्त नोमोग्राम चित्र-5 में दिखाया गया है। आप देखेंगे कि यहाँ पैमानों में अंकन एक समान नहीं है।
दो रेखाएँ यह दर्शाने के लिए खींची गई हैं कि किस प्रकार 2 x 3 = 6 और 9 x 4 =36 होते हैं।
कई प्रकार के द्विपरिवर्तनीय फलन के लिए नोमोग्राम बनाए जा सकते हैं, और कभी-कभी इसमें काफी कठिन गणित की आवश्यकता पड़ सकती है।
कदाचित नोमोग्राम का सबसे लोकप्रिय प्रकार ‘स्लाइड रूल’ है, जिसका यद्यपि इस प्रकार उल्लेख नहीं होता है। इसका आविष्कार उन्नीसवीं सदी में हुआ था और कई पीढ़ियों तक यह इंजीनियरों और वैज्ञानिकों के लिए अत्यावश्यक उपकरण के रूप में जाना जाता रहा। बीसवीं सदी के आधे से ज़्यादा दौर में इंजीनियर की छवि यही थी कि व्यक्ति जिसकी जेब से ‘स्लाइड-रूल’ झाँकता हो। प्रसिद्ध अनुवांशिकी वैज्ञानिक जिम वॉटसन और फ्रांसिस क्रिक ने भी नोबल पुरस्कार के लिए ‘स्लाइड-रूल’ से अपने डबल हेलिकल अनुवांशिकी मॉडल की ओर इशारा करते हुए नाटकीय अन्दाज़ में फोटो खिंचवाया था।
परन्तु इतिहास की अपनी विडम्बनाएँ होती हैं, आज ‘स्लाइड-रूल’ चलन में नहीं रहे। बच्चों, यहाँ तक कि बहुते से बड़ों ने भी शायद ही इसे देखा हो। इलेक्ट्रॉनिक क्रान्ति का यही कमाल है!
शैलेश ए. शिराली: रिशी वैली स्कूल (के.एफ.आई.) में गणित पढ़ाते हैं। 1996 में मुम्बई में आयोजित अन्तर्राष्ट्रीय गणित ओलम्पियाड की प्रॉब्लम कमेटी के अध्यक्ष रहे हैं। साथ ही, 1997 और 1998 में अन्तर्राष्ट्रीय गणित ओलम्पियाड में भाग लेने वाले भारतीय समूह का नेतृत्व किया है।
अँग्रेज़ी से अनुवाद: श्रीकान्त आप्टे: स्वतंत्र लेखक हैं। नाटक लेखन में रुचि। भोपाल में निवास।
यह लेख ‘मैथेमैटिकल मार्वल्स, ए प्रायमर ऑन लॉगेरिथ्म्स’ पुस्तक से साभार।
प्रकाशक: युनिवर्सिटीज़ प्रेस (इंडिया) प्राइवेट लिमिटेड, 2002।