विवेक मेहता
 ठीक से याद नहीं लेकिन स्कूल का ही कोई साल था। कहीं से खबर मिली कि चाँद पर प्लॉट बेचे जा रहे हैं। पता नहीं कितनी सही थी, लेकिन हम दोस्तों ने बड़े मज़े लिए थे इस खबर के कि बताओ भला कौन बेच रहा है चाँद पर प्लॉट, और कौन है जो खरीद रहा है।
ठीक से याद नहीं लेकिन स्कूल का ही कोई साल था। कहीं से खबर मिली कि चाँद पर प्लॉट बेचे जा रहे हैं। पता नहीं कितनी सही थी, लेकिन हम दोस्तों ने बड़े मज़े लिए थे इस खबर के कि बताओ भला कौन बेच रहा है चाँद पर प्लॉट, और कौन है जो खरीद रहा है।
वैसे चाँद पर प्लॉट बेचने की बात उस समय और आज भी कितनी ही मज़ाकिया लगे, पृथ्वी पर ज़मीन बेचना और खरीदना बेहद ही सीरियस बिज़निस है। यह बात और है कि शायद किसी और ग्रह के या धरती पर ही किसी अलग तरह की व्यवस्था के बाशिन्दों को हमारी यह व्यवस्था मज़ाकिया लगे।
मैं इन दिनों जिस यूनिवर्सिटी कैम्पस में पढ़ाता व रहता हूँ, उसके बनने के पहले कैंपस व आसपास की ज़मीन पर लोग खेती किया करते थे। लेकिन धीरे-धीरे इन पच्चीस सालों में ज़मीन का इस्तेमाल खेती से इतर कई और कारणों में होने लगा है। दुकानें (स्थाई-अस्थाई), मार्केट, ढाबे, नर्सरी, मकान (कच्चे-पक्के), स्कूल, गलियाँ-सड़कें, मन्दिर-मस्जिद-चर्च, कब्रिस्तान इत्यादि में। इसके अलावा कई लोगों ने ज़मीन के बड़े-बड़े प्लॉट खरीदकर, बाउंड्री-वॉल बनवाकर यूँ ही खाली छोड़ रखे हैं।
इन सबके चलते देखते-ही-देखते ज़मीन की कीमतें काफी बढ़ गईं। इस उछाल का अन्दाज़ा इस बात से लगाया जा सकता है कि यूनिवर्सिटी गेट से मात्र एक-डेढ़ कि.मी. की दूरी पर एक बिल्डर 75 लाख से लेकर 95 लाख तक के विला बनाकर बेच रहा है।
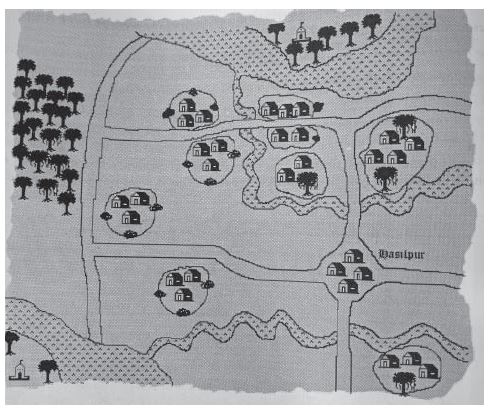
यूनिवर्सिटी के आसपास के गाँवों के लोग अक्सर ही ज़मीन खरीदने-बेचने की बात करते मिल जाते हैं। अभी कुछ ही दिन पहले मेरी गली में फूल-पौधों का ध्यान रखने वाले साथी प्रदीप और मेरे घर पर दूध देने वाले साथी पूबेरून मेरे घर पर आपस में बतिया रहे थे। मैं उनकी बातें सुन रहा था। प्रदीप कह रहे थे कि वे यूनिवर्सिटी के पास आकर रहना चाहते हैं। दूर से आकर काम करने में दिक्कत होती है और काम भी कम है। ज़मीन तो बहुत महंगी है, इसीलिए किराए का घर ही ढूँढ़ रहे हैं। उनकी बातें सुनकर मुझे अचानक से एक ख्याल आया और मैं एक कागज़ पर एक चित्र बनाकर उन दोनों के पास ले गया। वो चित्र कुछ ऐसा था (चित्र 1)। इस चित्र में मैंने दो समानान्तर किनारों (एक ओर नदी और दूसरी ओर सड़क) के बीच में तीन प्लॉट बनाए। तीनों प्लॉट के चारों साइडों का माप भी दर्शा दिया। मेरी मंशा थी कि मैं उन लोगों से जो कि ज़मीन खरीदने-बेचने का व्यवहारिक ज्ञान रखते हैं, उनकी समझ इन प्लॉटों के बारे में, खास तौर पर परिधि व क्षेत्रफल से जुड़ी हुई, जानूँ।
इस चित्र में मैंने दो समानान्तर किनारों (एक ओर नदी और दूसरी ओर सड़क) के बीच में तीन प्लॉट बनाए। तीनों प्लॉट के चारों साइडों का माप भी दर्शा दिया। मेरी मंशा थी कि मैं उन लोगों से जो कि ज़मीन खरीदने-बेचने का व्यवहारिक ज्ञान रखते हैं, उनकी समझ इन प्लॉटों के बारे में, खास तौर पर परिधि व क्षेत्रफल से जुड़ी हुई, जानूँ।
इन दो साथियों के अलावा मैंने इस चित्र पर अन्य कई लोगों से, दो या ज़्यादा के समूहों में, बात की। इनमें हार्डवेयर, किराने की दुकान चलाने वाले साथी, तकनीकी संस्थान में वर्कशॉप व लैब सम्भालने वाले साथी इत्यादि शामिल थे। उन लोगों की आपसी चर्चा में मुझे दो मुख्य बिन्दु मिले।
• पहला तो ये कि दिए गए विकल्पों में से लगभग सभी एक वर्गाकार प्लॉट को पसन्द करते हैं। वजह, बाकी दोनों प्लॉट में घर बनाने से कुछ ज़मीन बेकार जाएगी।
• एक दूसरी महत्वपूर्ण बात जो मुझे समझ में आई कि लोग प्लॉट के क्षेत्रफल को लेकर दुविधा में रहते हैं। उनकी यह दुविधा उनके द्वारा अपनाए गए दो तरीकों से परिलक्षित होती है –
(1) वे किसी वर्ग या आयत की तरह समचतुर्भुज या समानान्तर चतुर्भुज का क्षेत्रफल भी किनारों की माप के गुणनफल के बराबर निकालते हैं, व
(2) कई दफे वे क्षेत्रफल व परिमिति के बीच उलझ जाते हैं। वे परिमिति को क्षेत्रफल के माप के रूप में पेश करते हैं। अब इसके चलते होता यह है कि चित्र में दिखलाए गए तीन प्लॉटों में से जिस चतुर्भुज की परिमिति सबसे ज़्यादा है, उसका क्षेत्रफल साथियों के मुताबिक सबसे ज़्यादा निकलता है।
वैसे क्षेत्रफल और परिमिति के बीच का यह हेर-फेर कोई नई बात नहीं। आज से तकरीबन 1700 साल पहले यूक्लिड की लिखी किताब एलीमेंटस पर अपनी टिप्पणी देते हुए यूनानी दार्शनिक प्रोक्लोस एक चेतावनी-सी देते हुए लिखते हैं:
| बॉक्स-1 उदाहरण के तौर पर अगर ऐसे इन तीन आयतों की तुलना की जाए जिनकी लम्बाई व चौड़ाई नीचे दिए गए चित्र में दर्शाई गई है, तो हम पाते हैं कि 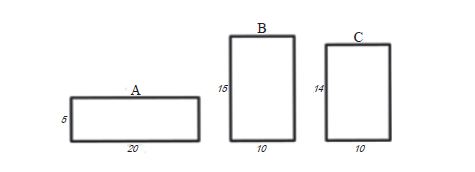 • आयत A व B, दोनों की परिमिति समान है, लेकिन उनका क्षेत्रफल अलग-अलग है; • आयत C की परिमिति अन्य आयतों की तुलना में कम है, लेकिन उसका क्षेत्रफल जहाँ आयत A से ज़्यादा है परन्तु आयत B से कम। |
हम अक्सर ही, ज़मीन आवंटन के दौरान, क्षेत्रफल को परिमिति के बराबर मान लेने की गलती को पकड़ने में चूक जाते हैं; नतीजतन ऐसे कई लोग हैं जिन्होंने छोटे हिस्से की तुलना में ज़मीन के बड़े हिस्से पर कब्ज़ा पा लिया है, वो भी इस ‘न्यायसंगत’ आधार पर कि सौदा बराबरी का था क्योंकि दोनों हिस्सों की परिमिति समान थी।
साफ ज़ाहिर है कि एक बराबर परिमिति के दो क्षेत्रफल भी बराबर हों, ये कतई ज़रूरी नहीं। और तो और, एक कम परिमिति वाला क्षेत्रफल किसी ज़्यादा परिमिति वाले क्षेत्रफल से ज़्यादा भी हो सकता है।
ईसा से 100 से ज़्यादा वर्ष पूर्व के यूनान के इतिहासकार पोलीबियस अपनी प्रसिद्ध इतिहास की चौथी पुस्तिका में लिखते हैं:
ज़्यादातर लोग शहरों के साईज़ का अन्दाज़ा उसकी परिमिति से लगाते हैं। ऐसे में अगर कोई उन से कहे कि मेगेलोपोलिस की परिमिति 50 स्टेड्स1 (लगभग पाँच मील) और स्पार्टा की 48 है, लेकिन स्पार्टा मेगेलोपोलिस का लगभग दोगुना है, तो वे अचम्भित रह जाते हैं।
एक ऐसे माहौल में जब दार्शनिक व इतिहासकार क्षेत्रफल और परिमिति की समस्या को देख-समझ पा रहे थे, तब गणितज्ञ भला इस सवाल से कैसे बचते। गणितज्ञ भी क्षेत्रफल, परिमिति व आयतन से जुड़े तमाम सवालों पर सोच रहे थे और हल करने की कोशिश में लगे थे।
उनमें से एक सवाल जो कि सीधे-सीधे किसी आयत की परिमिति व क्षेत्रफल से जुड़ा हुआ था वो था कि किसी दी गई परिमिति के लिए वह कौन-सा आयत होगा जिसका क्षेत्रफल सबसे ज़्यादा होगा? उदाहरण के लिए बॉक्स-1 में दिखलाए गए आयत A व B की परिमिति 50 है, लेकिन क्षेत्रफल अलग-अलग है। तो सवाल बनता है कि 50 परिमिति का ऐसा कौन-सा आयत होगा जिसका क्षेत्रफल सबसे ज़्यादा हो?2
इस सवाल का एक जुड़वाँ भाई भी है। जुड़वाँ इसलिए कि दोनों सवालों का उत्तर एक ही है। वो जुड़वाँ सवाल यह है कि किसी दिए गए क्षेत्रफल के लिए ऐसा कौन-सा आयत होगा जिसकी परिमिति सबसे कम हो?
गौर कीजिए कि ये दोनों ही सवाल किसी राशि के उच्चतम या निम्नतम मान से जुड़े हुए हैं। आधुनिक गणित के छात्र ऐसे सवालों को हल करने के लिए अवकलन गणित (Differential calculus) का उपयोग करते हैं। लेकिन ऐसे सवालों में अवकलन गणित का उपयोग तो सत्रहवीं शताब्दी के बाद की बात है। और हम बात कर रहे हैं ईसा पूर्व की।
बीजगणित (Algebra) जिसका इतिहास ईसा से भी पुराना है, का इस्तेमाल कर हम इस सवाल का जवाब निकाल सकते हैं कि किसी दी गई परिमिति के लिए वह कौन-सा आयत होगा जिसका क्षेत्रफल सबसे ज़्यादा हो (देखें बॉक्स 2)। वैसे बॉक्स देखने से पहले आप शायद खुद एक कोशिश करना चाहें जवाब निकालने की।

बॉक्स 2 में हमने देखा कि एक वर्ग अपने आप में इस मायने में भी खास है कि एक बराबर परिमिति के सभी आयतों में वर्ग का क्षेत्रफल अधिकतम होता है। अब आते हैं जुड़वे सवाल पर कि किसी दिए गए क्षेत्रफल के लिए ऐसा कौन-सा आयत होगा जिसकी परिमिति सबसे कम हो? जैसा कि मैंने पहले ही कहा कि इस सवाल का जवाब भी वर्ग ही होगा। लेकिन अगर हम सीधी रेखाओं का मोह त्याग दें तो क्या हम वर्ग से बेहतर भी कर सकते हैं? उदाहरण के लिए, एक दी गई परिमिति के लिए किसी वर्ग व वृत्त में से वृत्त का क्षेत्रफल ज़्यादा होता है। क्या आप ये सिद्ध कर सकते हैं? क्या इस सवाल का जवाब बिना अवकलन गणित का इस्तेमाल किए निकाल सकते हैं? (देखें बॉक्स 3)

विवेक कुमार मेहता: आई.आई.टी. कानपुर से मेकेनिकल इंजिनीयरिंग में पीएच.डी. की है एवं तेजपुर विश्वविद्यालय, असम में पढ़ा रहे हैं।