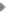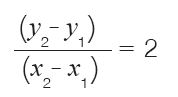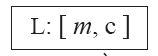विवेक मेहता[Hindi,PDF 245KB]
भाग-1
लाइनें ही लाइनें
हमारे अपने तीन-आयामी (असल में चार, समय को जोड़कर) संसार में लाइनें हर कहीं दिख जाती हैं। अगर आप किसी कमरे में बैठकर यह लेख पढ़ रहे हैं तो उस कमरे की कोई भी दो दीवारें या ऐसे ही दो समतल जहाँ मिल रहे हों, आपको एक लाइन दिख जाएगी। जब आसमान में एक हवाई जहाज़ उड़ता है तो अपने पीछे एक सफेद लकीर छोड़ता जाता है। दो पेड़ों के बीच कपड़े सुखाने के लिए तानकर बाँधी गई एक रस्सी भी एक लाइन को ही दर्शाती है।
ऐसे ही कुछ दिन पहले जब मैं एक कागज़ पर चन्द लाइनें खींचकर कुछ सोच रहा था तो मेरा मन किया कि इन अमूर्त लाइनों को मैं एक-एक नाम दूँ। मैंने इन लाइनों को L1, L2, L3 सरीखे नाम दे दिए (चित्र-1)। लेकिन फिर मुझे लगा कि ऐसा नामकरण तो बड़ा सतही है। ऐसे नाम रखने से तो इन लाइनों के बारे में कुछ भी पता नहीं चलता। ऐसा क्या है जो इन लाइनों को खास बनाता है। या फिर किन मायनों में ये लाइनें एक-दूसरे से अलग और किन मायनों में समान हैं। इस नामकरण के तरीके से तो यह पता ही नहीं चलता। अगर नामकरण कुछ ऐसा हो कि इन सभी लाइनों को उनके तमाम गुणों के साथ एक-दूसरे से अलग-अलग पहचाना जा सके तो फिर बात ही क्या1।
लेकिन क्या लाइनों के नामकरण का कुछ ऐसा तरीका हो सकता है जिससे हम किसी लाइन के तमाम गुणों को जान सकें या ये कहें कि एक लाइन को पूरी तरह परिभाषित कर सकें व उसे अन्य लाइनों से अलग पहचान सकें? आइए देखते हैं।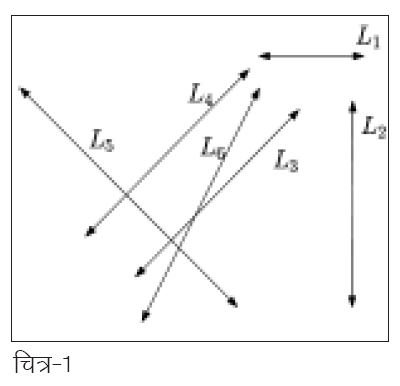
सबसे पहले समझने की कोशिश करते हैं कि आखिर वह कौन-सी बातें हैं जो समतल पर किसी एक लाइन को एक दूसरी लाइन से अलग करती हैं।
चित्र-2 में दो लाइनों को दो अलग-अलग परिस्थितियों में दिखलाया गया है। इन परिस्थितियों की पड़ताल कर हम उन खास बातों को पहचान सकते हैं जो एक लाइन को किसी दूसरी लाइन से अलग करती हैं। आगे बढ़ने से पहले आप चाहें तो कोशिश कर देख सकते हैं कि क्या आप उन बातों को पहचान सकते हैं।
सबसे पहले तो यह देख लें कि चित्र 2(a) व 2(b) क्या दर्शा रहे हैं। असल में ये चित्र उन दो स्थितियों को प्रदर्शित कर रहे हैं जिसमें एक समतल पर कोई दो लाइनें हो सकती हैं: (1) पहली परिस्थिति जिसमें दो लाइनें एक-दूसरे को समतल के किसी बिन्दु पर काटें व (2) दूसरी परिस्थिति जिसमें ये रेखाएँ समानान्तर हों यानी कि समतल पर ऐसा कोई भी बिन्दु ना हो जिस पर ये एक-दूसरे को काटें। केवल यही दो परिस्थितियाँ सम्भव हैं। आप चाहें तो कोशिश कर देख सकते हैं कोई अन्य परिस्थिति खोजने की। आइए अब ज़रा देखते हैं इन परिस्थितियों में जो दो लाइनें दिखलाई गई हैं, वो कैसे अलग-अलग हैं।
चित्र-2(a), जिसमें दोनों रेखाएँ एक-दूसरे को बिन्दु ग्र् पर काट रही हैं, में लाइनें L1 व L2 अलग इसलिए अलग नज़र आ रही है क्योंकि उनके बीच के कोण का मान शून्य नहीं है। अगर इनके बीच का कोण शून्य के बराबर होता तो ये दोनों एक-दूसरे के ऊपर एकदम फिट बैठ जातीं व असल में एक ही रेखा या लाइन को दर्शा रही होतीं 2।
इसी तरह चित्र-2(b) में हम पाएँगे कि समानान्तर होने के चलते इन लाइनों के बीच का कोण तो शून्य है लेकिन इनके बीच एक दूरी है जिसकी वजह से ये रेखाएँ अलग-अलग दिखाई दे रही हैं। अगर यह दूरी शून्य होती तो उस स्थिति में लाइनें L1 व L2 अलग-अलग लाइनें नहीं बल्कि एक ही रेखा को दर्शा रही होतीं।
इस चर्चा से यह समझ बनती है कि जो दो बातें एक लाइन से दूसरी लाइन को अलग करती हैं उनमें से एक का लेना-देना कोण से है तो दूसरी का दूरी से। तो क्या हम समतल पर खींची लाइनों का नामकरण इन दोनों मापों, कोण व दूरी, की मदद से कर सकते हैं? और इस सवाल का जवाब है - हाँ। लेकिन इस नामकरण की व्यवस्था के लिए भी किसी अन्य व्यवस्था की ही तरह ज़रूरत होगी एक सन्दर्भ की जिसके सापेक्ष हम लाइनों का नाम रखेंगे। इस प्रक्रिया के दौरान यह समझना बहुत ज़रूरी है कि नामों को उनके खास सन्दर्भ में ही देखा जाना चाहिए। जैसा कि हम आगे देखेंगे अलग-अलग सन्दर्भों में लाइनों के नाम अलग-अलग होते हैं और अगर लाइनों को उनके सन्दर्भ से जोड़कर ना देखा जाए तो गड़बड़ हो सकती है3। 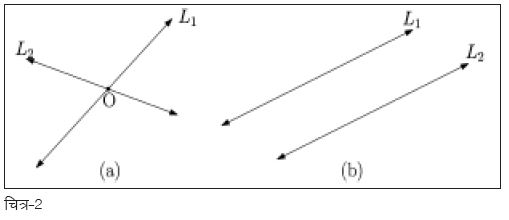
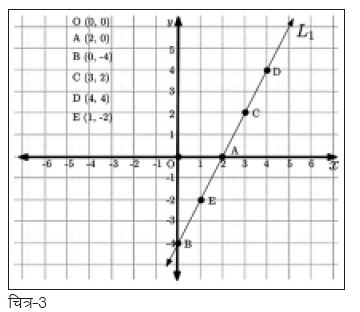
चित्र-3 में एक ग्राफ पेपर पर एक-दूसरे पर परस्पर लम्ब दो सन्दर्भ-अक्ष लिए गए हैं - अक्ष-x व y ।4 जिनके सापेक्ष लाइन L1 व उसके कुछ बिन्दुओं को दर्शाया गया है5। इस व्यवस्था में किसी भी सामान्य बिन्दु P की स्थिति को (x, y) से दर्शाते हैं जहाँ x व y क्रमश: सन्दर्भ अक्ष-x व y से जुड़े दो निर्देशांक हैं। उदाहरण के लिए बिन्दु c के निर्देशांक हैं (3, 2) जो ग्राफ पर इसकी स्थिति को दर्शा रहे हैं। किसी अन्य ज्ञात बिन्दु से इस बिन्दु तक पहुँचने के लिए हमें इन निर्देशांकों का इस्तेमाल करना होगा। अगर बिन्दु O, जिसके निर्देशांक (0, 0) हैं, से शुरु करके हम सन्दर्भ अक्ष- x की दिशा में 3 कदम व फिर सन्दर्भ अक्ष-y की दिशा में 2 कदम चलें तो हम बिन्दु c तक पहुँच जाएँगे। या फिर पहले सन्दर्भ अक्ष- y की दिशा में 2 कदम चलकर फिर सन्दर्भ अक्ष-x की दिशा में 3 कदम चलने से भी हम बिन्दु c तक पहुँच जाएँगेे। आइए अब इस चित्र के सन्दर्भ में हम एक लाइन के गुणों को पहचानने की कोशिश करते हैं।
* एक और बात जो किसी भी लाइन पर लागू होती है कि लाइन पर किसी भी दो बिन्दुओं (x1, y1) व (x2, y2) के लिए अनुपात
(y2 - y1) / (x2 - x1)
एक नियत राशि होगा। लाइन ख्र्1 के मामले में यह अनुपात 2 के बराबर होगा, जिसका मतलब हुआ कि अक्ष- x की दिशा में अगर हम एक कदम आगे बढ़ें तो लाइन पर अक्ष-y की दिशा में दो कदम आगे बढ़ जाते हैं। उदाहरण के तौर पर अगर हम बिन्दु C (3, 2) व D (4, 4) को लें तो Y2 - Y1 = 4-2 = 2
व
X2 - X1 = 4-3 = 1 होगा।
इन मानों के लिए
लिए होगा। ठीक इसी तरह अगर हम बिन्दुओं E (1, -2) व C (3, 2) को लें तो देखेंगे कि इस मामले में भी अनुपात का मान 2 ही आएगा (करके देखिए)।
गणितिय भाषा में इस अनुपात को किसी लाइन की ढलान (slope) कहते हैं व इसका मान इस बात पर निर्भर करता है कि अक्ष-x व लाइन के बीच कितने अंश का कोण बन रहा है8 (चित्र-4)। इस ढलान को सामान्यत: m से दर्शाते हैं व यह ढलान दर्शाती है कि राशि x के बदलने के साथ-साथ राशि y में होने वाले परिवर्तन की दर क्या है9।
एक बात पर गौर कीजिए कि लाइन L1 को किसी ऐसे सन्दर्भ-तंत्र में भी दर्शाया जा सकता है जिसमें सन्दर्भ अक्षों-x व y की स्थिती ग्राफ पर कुछ अलग हो, जैसा कि चित्र-5 में दिखाया गया है। यकीनन इन सन्दर्भ-तंत्रों में लाइन L1 के बिन्दुओं की स्थिति भिन्न होगी। ये ठीक वैसा ही होगा अगर हम किसी एक ही वस्तु को अलग-अलग जगहों से देखें। लेकिन इनमें व ऐसे किसी भी अन्य सन्दर्भ-तंत्र में एक लाइन के गुण तो वही होंगे जिनकी चर्चा हमने अभी-अभी की। हाँ, इन गुणों के मान अलग-अलग सन्दर्भ-तंत्र में अलग-अलग होंगे।
वैसे क्या इसके अलावा भी आप लाइनों के कुछ अन्य गुण सुझा सकते हैं? आप शायद कहें कि एक लाइन पर अनगिनत बिन्दु होते हैं। बात बिलकुल सही है लेकिन हम चाहकर भी इन सभी को लिख नहीं सकते, क्योंकि ये अनगिनत जो ठहरे। पर वहीं दूसरी तरफ ऐसा करने की ज़रूरत भी नहीं है। हमने जिन दो गुणों को अभी-अभी पहचाना है, उनकी मदद से किसी भी लाइन पर पड़ने वाले तमाम बिन्दुओं की गणना की जा सकती है। आइए देखते हैं कैसे।
हमने देखा कि एक लाइन की ढलान m नियत होती है। यानी कि लाइन पर किन्हीं भी दो बिन्दुओं के लिए (y2- y1) / (x2- x1) = m होता है।
इसे सरल कर हम समीकरण (1) की शक्ल में कुछ इस तरह भी लिख सकते हैं:
Y2 - Y1 = m (X2- X1)
या
y2 = m (x2 - x1) + y1 ---------(1)
समीकरण (1) की पड़ताल कर हम देख सकते हैं कि अगर किसी लाइन के लिए हमें उसकी ढलान थ्र् का मान व साथ ही उस लाइन पर एक बिन्दु (x1 , y1) पता हो तो हम उस लाइन पर पड़ने वाले किसी भी अन्य बिन्दु की गणना कर सकते हैं। आइए एक उदाहरण से समझते हैं।
मान लीजिए कि चित्र-3 में दिखलाई हुई लाइन L1 के लिए हमें पता हो कि इस लाइन की ढलान यानी कि m = 2 है व यह लाइन बिन्दु E (1, -2) से होकर गुज़रती है। अब इतनी जानकारी के साथ हम यह जानना चाहते हैं कि लाइन पर ऐसा कौन-सा बिन्दु होगा जिसके लिए x= 3 हो। क्या आप कोई तरीका सुझा सकते हैं?
ग्राफ से यह जानने का तरीका बड़ा आसान है। चित्र-6 की तरह अक्ष-न् पर बिन्दु x = 3 से अक्ष-y के समानान्तर एक रेखा खींच लो। वो रेखा जिस किसी बिन्दु पर लाइन L1 को काटे, वही हमारा उत्तर होगा। इस तरह हमें जो बिन्दु मिलेगा वो होगा (3, 2) यानी कि बिन्दु क्।
लेकिन इस सवाल का जवाब हम बिना ग्राफ बनाए समीकरण (1) की मदद से भी निकाल सकते हैं। हमें पता है कि दी हुई लाइन बिन्दु (1, -2) से होकर गुज़रती है। हम इस दिए हुए बिन्दु को (x1 , y1) मान लेते हैं। समीकरण (1) में x1 व y1 का मान रखने पर हमें मिलेगा:
y2 = 2 (x2 - 1) + (-2)
या
y2 = (2x2 - 4) ---------------(2)
आप गौर करें तो देखेंगे समीकरण (2) के दाहिने भाग में आने वाली पहली राशि तो ढलान से सम्बन्धित है लेकिन दूसरी राशि का मान बिन्दु ए यानी कि उस बिन्दु के x हिस्से यानी कि -4 के बराबर है। ए वह बिन्दु है जिस पर लाइन L1 अक्ष-y को काटती है10।
समीकरण (2) में हम x2 का मान रखकर y2 का मान निकाल सकते हैं या फिर y2 का मान पता हो तो x2 का मान निकाल सकते हैं। ऊपर सवाल पूछा गया था कि लाइन L1 पर ऐसा कौन-सा बिन्दु होगा जिसके लिए x = 3 हो? समीकरण (2) में x2 = x = 3 रखने पर हमें मिलेगा:
y2 = 2 x 3 - 4 = 2
तो हमारा जवाब हुआ कि लाइन L1 पर ऐसा बिन्दु जिसके लिए x = 3 हो (3, 2) होगा। गौर कीजिए कि यही उत्तर हमें ग्राफ से भी मिला था। इसी तरह समीकरण (2) की मदद से हम लाइन पर कोई भी बिन्दु निकाल सकते हैं। सामान्यीकरण करते हुए समीकरण (2) को हम कुछ इस तरह लिख सकते हैं:
y = mx+c(3)
समीकरण (3) एक समतल पर किसी भी ऐसी लाइन के लिए लागू होता है जिसके लिए m दी गई लाइन की ढलान व c y-अन्त:-खण्ड है। ध्यान दीजिए कि m का समबन्ध कोण से है व c एक दूरी को दर्शाता है। किसी लाइन के लिए सिर्फ इन दो राशियों के ज्ञात होने भर से ही हम उसके तमाम गुणों का पता लगा सकते हैं। तो क्यों न हम लाइनों के नाम कुछ ऐसे दें:
इस नामकरण के चलते लाइन L1 का नाम होगा:
L: [2-4]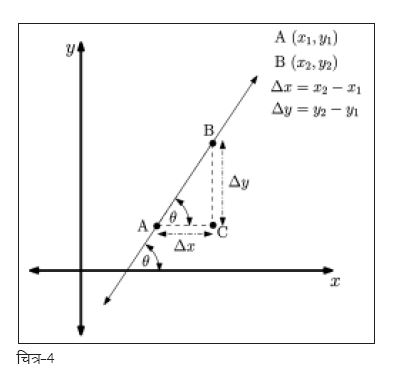
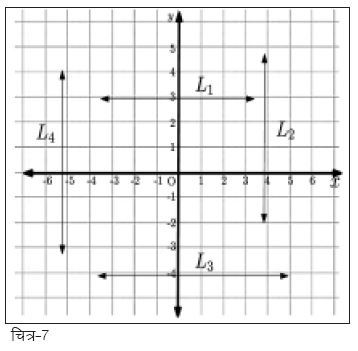
इस बिन्दु पर उन खास लाइनों पर भी बात कर लेनी चाहिए जिनका ज़िक्र हमने पहले किया था यानी कि ऐसी रेखाएँ जो दोनों अक्षों में से सिर्फ किसी एक को काटती हैं। किसी ग्राफ में ऐसी रेखाओं को हम आसानी से देख सकते हैं। ऐसी रेखाएँ दोनों अक्षों में से किसी एक अक्ष के समानान्तर होती हैं। चित्र-7 में कुछ ऐसी ही लाइनें दिखलाई गई हैं। इनमें से लाइन L1 व L3 के ढलान 0 (शून्य) हैं व लाइन L2 व L4 के ढलान अपरिभाषित हैं। ऐसा इसलिए क्योंकि लाइन L1 व L3 पर किन्हीं भी दो बिन्दुओं के लिए (y2 - y1) शून्य होगा तथा लाइन L2 व L4 पर किन्हीं भी दो बिन्दुओं के लिए (x2 - x1) शून्य होगा। इसके अलावा आप देखेंगे कि लाइनें L1 व L3, जो अक्ष-x के समानान्तर हैं उनके लिए y-अन्त:-खण्ड निकाला जा सकता है, क्योंकि ऐसी रेखाएँ एक निश्चित बिन्दु पर अक्ष-y को काटती हैं। वहीं दूसरी ओर ऐसी लाइनें जो कि अक्ष-y के समानान्तर हैं, यानी कि L2 व L4, उनके लिए y-अन्त:-खण्ड परिभाषित ही नहीं होगा क्योंकि ऐसी रेखाएँ किसी भी बिन्दु पर अक्ष-y को नहीं काटेंगी।
अब चूँकि लाइनों के लिए बनाई गई नामकरण की हमारी व्यवस्था लाइन की ढलान व y-अन्त:-खण्ड से जुड़ी हुई है इसीलिए ऐसी लाइनें जो अक्ष-yके समानान्तर हों, यानी कि जिनके लिए ढलान व y-अन्त:-खण्ड, दोनों ही परिभाषित ना हों, हमें एक अलग तरीका निकालना होगा। मेरे दिमाग में जो एक तरीका आ रहा है कि हम ऐसी लाइनों को सिर्फ एक संख्या से ही परिभाषित करें12। और वो संख्या होगी लाइन के x-अन्त:-खण्ड के बराबर। अगर अक्ष-y के समानान्तर किसी लाइन के लिए x-अन्त:-खण्ड ‘p’ के बराबर हो तो हम इसे L: [p] नाम दे सकते हैं। जिस किसी लाइन का नाम हमें सिर्फ एक संख्या के साथ मिलेगा, हम समझ जाएँगे कि इस लाइन के लिए ढलान व yअन्त:-खण्ड, दोनों ही अपरिभाषित हैं व इस लाइन के हर एक बिन्दु के लिए x = p होगा।
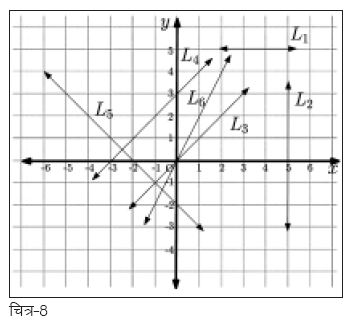
लाइनों के नामकरण की यह व्यवस्था बना लेने के बाद उन लाइनों (चित्र-1) को नाम दे देते हैं जिनसे हमने शुरुआत की थी। चित्र-1 की लाइनों को एक ग्राफ पर दर्शाने से हमें चित्र-8 वाली स्थिति मिलेगी। इस ग्राफ से हम आसानी से सभी लाइनों के लिए ढलान व yअन्त:-खण्ड निकालकर उनके नाम रख सकते हैं (तालिका-1)।
इन नामों से इन सभी लाइनों की तुलना उनके गुणों के आधार पर की जा सकती है और हम इन लाइनों को एक-दूसरे से अलग पहचान भी सकते हैं। जैसे कि ध्यान दीजिए उन लाइनों में जिनके लिए ढलान परिभाषित है सिर्फ लाइन L5 की ढलान ऋणात्मक है यानी कि सिर्फ इस लाइन के लिए ही x के बढ़ने के साथ-साथ y घट रहा है। बाकी सभी लाइनों के लिए या तो x के बढ़ाने के साथ-साथ y भी बढ़ रहा है (धनात्मक ढलान) या फिर एक समान बना हुआ है (शून्य ढलान)। इसी तरह हम देख सकते हैं कि लाइन L3 व L6 दोनों अक्ष-y को एक ही बिन्दु ग्र् पर काट रही हैं यानी कि उनके y-अन्त:-खण्ड एक बराबर (इस मामले में शून्य) हैं, लेकिन उनकी ढलान अलग-अलग हैं। अगर इस बिन्दु को हम शुरुआती बिन्दु माने तो x के बढ़ने के साथ-साथ उस लाइन के लिए y तेज़ी से बढ़ेगा जिसकी ढलान ज़्यादा होगी। लाइन L6 की ढलान L3 की दोगुनी है। इसका मतलब हुआ कि x के बढ़ने के साथ-साथ लाइन L6 के लिए y लाइन L3 की तुलना में दोगुनी तेज़ी से बढ़ेगी।
क्या हमारी लाइनें भी कुछ दर्शाती हैं?
क्या ग्राफ पर खींची गई लाइनें भी कुछ दर्शाती हैं? अगर आपने गौर किया हो तो समीकरण (3)
Y=mx+c
एक सम्बन्ध को दर्शाता है - चर-राशि y और x के बीच के सम्बन्ध को। दो राशियों के बीच के सम्बन्ध को दर्शाने वाला यह सबसे सरल समीकरण है13। इस समीकरण की मदद से आप किसी दी गई लाइन के लिए जान सकते हैं कि राशि न् के बदलने के साथ-साथ y में कैसा परिवर्तन आ रहा है। दो सन्दर्भ रेखाओं की व्यवस्था का इस्तेमाल करने का यही वो अतिरिक्त फायदा है जिसका ज़िक्रहमने पहले किया था। एक सरल व्यवहारिक उदाहरण लेकर इस सम्बन्ध को समझने की कोशिश करते हैं।
मान लीजिए कि आपको एक नई गुल्लक मिलती है जिसमें पहले से ही 99 रुपए हैं। आप तय करते हैं कि हर दिन आप उस गुल्लक में एक रुपया तब तक डालेंगे जब तक कि गुल्लक में 500 रुपए नहीं हो जाते। अगर आप हिसाब लगाने जाएँ तो 1 दिन बाद गुल्ल्क में 100 रुपए होंगे, 2 दिनों बाद 101 रुपए, 5 दिनों बाद 104 रुपए। है ना! इस तरह हर दिन के लिए रुपयों का हिसाब लगाकर एक ग्राफ पेपर पर इन संख्याओं को दर्शाएँ तो चित्र-9 में लाइन L1 मिलेगी। क्या ग्राफ देखकर आपको आश्चर्य हुआ कि सारे बिन्दु एक लाइन L1 पर ही क्यों पड़ रहे हैं? वैसे अगर आपने हिसाब लगाते हुए इस बात पर गौर किया हो कि आप असल में समीकरण (3) ही हल कर रहे हैं तो इसमें कोई आश्चर्य की बात नहीं। आइए देखते हैं कैसे। चित्र-9 में दर्शाई गई लाइन L1 का नाम होगा L: [1, 99]। यानी कि इस लाइन की ढलान m = 1 और y-अन्त:-खण्ड c = 99। अगर इस लाइन के लिए समीकरण लिखने जाएँं तो हमें मिलेगा:
y = 1xx + 99 ---------------(4)
इस उदाहरण में ‘y’ गुल्लक में जमा रुपए, ‘x’ को दिनों की संख्या, ढलान m = 1 गुल्लक में रुपए बढ़ने की दर यानी कि 1 रुपया प्रतिदिन, व c = 99 रुपयों के शुरुआती मान को दर्शा रही है।
अगर शुरुआत में आप यह तय करते कि हर दिन आप गुल्लक में एक नहीं बल्कि दो रुपए डालेंगे तो चित्र-9 के ग्राफ में हमें लाइन L2 मिलती। साफ ज़हिर है इस दर से गुल्लक में रुपए डालते हुए आप कम दिनों में ही 500 रुपए के लक्ष्य तक पहुँच जाते।
तो देखा आपने हमारी लाइनें भी कुछ दर्शाती हैं: दो राशियों के बीच के सम्बन्ध को। अगर आप इस सम्बन्ध को समझ पाए होंगे तो चित्र-10 में दिखाए गए ग्राफ में दिनों के साथ-साथ गुल्लक में रखे रुपयों में होने वाले परिवर्तन पर एक कहानी लिख पाएँगे।
कुछ सवाल
1. अगर आपके दोस्त और आपकी गुल्लक में रखे रुपयों की संख्या को क्रमश: लाइन L:[3, 99], व L:[4, 80] से दर्शाया जा सके तो आपकी और आपकी दोस्त की गुल्लक में कितने दिनों बाद एक बराबर रुपए होंगे?
2. लाइन L: [ 2, -4 ] के लिए न्-अन्त:-खण्ड क्या होगा?
3. क्या लाइन L: [1, -4 ], व L: [ 1, 0 ] एक-दूसरे को ग्राफ के किसी बिन्दु पर काटेंगी?
4. लाइन L: [ 1, -4 ], व L: [ 2, 1 ] एक-दूसरे को ग्राफ के किस बिन्दु पर काटेंगी?
5. क्या लाइन L: [ 2, -4 ] पर ऐसा कोई बिन्दु होगा जिसके लिए x = y हो?
6. वो लाइनें कैसी होंगी जिन पर ऐसा कोई भी बिन्दु ना हो जिसके लिए x = y हो?
विवेक मेहता: आई.आई.टी., कानपुर से मेकेनिकल इंजीनियरिंग में पीएच.डी. की है। एकलव्य के विज्ञान शिक्षण कार्यक्रम के साथ फैलोशिप पर हैं जिसके तहत वे हाईस्कूल की कक्षाओं के लिए गतिविधि आधारित मॉड्यूल तैयार कर रहे हैं। यह प्रयास, कनेक्ट्ड लर्निंग इनिशिएटिव, टाटा सामाजिक विज्ञान संस्थान के समर्थन से संचालित है।
आभार: कनेक्ट्ड लर्निंग इनिशिएटिव टीम के सभी साथियों - राजेश, दीपक, भास, उमा व हिमांशु का, जिनके सुझावों के चलते यह लेख अपने वर्तमान रूप में आ पाया।