विवेक मेहता
 मूमन ही हम सभी जाने-अनजाने आँकड़ों से रूबरू होते रहते हैं। चाहे किसी क्रिकेट मैच का स्कोर कार्ड हो, देश में गरीबी और बेरोज़गारी की स्थिति बतलाती अखबार या टीवी की खबरें हों, एक शिक्षिका के अपनी कक्षा के बच्चों से जुड़े रिकॉर्ड हों या फिर किसी परिवार के मासिक खर्च का हिसाब-किताब। आँकड़े हर कहीं हैं। ज़ाहिर तौर पर ये आँकड़े ज़रूरी हैं: खेल से जुड़े आँकड़े देखकर पता लगाया जा सकता है कि एक खिलाड़ी कैसा प्रदर्शन कर रहा है जिससे उसकी अगले मैच या सीरीज़ में खेलने की दावेदारी तय होती है; गरीबी या बेरोज़गारी के आँकड़े देश की सरकारों को अपनी नीति निर्धारित करने में मदद करते हैं; एक शिक्षिका आँकड़ों की मदद से अपने पढ़ाने के तरीके व कक्षा के बच्चों के प्रदर्शन के बीच सम्बन्ध देख सकती है और एक परिवार के खर्च से जुड़े आँकड़े उस परिवार का बजट बनाने में काम आते हैं।
मूमन ही हम सभी जाने-अनजाने आँकड़ों से रूबरू होते रहते हैं। चाहे किसी क्रिकेट मैच का स्कोर कार्ड हो, देश में गरीबी और बेरोज़गारी की स्थिति बतलाती अखबार या टीवी की खबरें हों, एक शिक्षिका के अपनी कक्षा के बच्चों से जुड़े रिकॉर्ड हों या फिर किसी परिवार के मासिक खर्च का हिसाब-किताब। आँकड़े हर कहीं हैं। ज़ाहिर तौर पर ये आँकड़े ज़रूरी हैं: खेल से जुड़े आँकड़े देखकर पता लगाया जा सकता है कि एक खिलाड़ी कैसा प्रदर्शन कर रहा है जिससे उसकी अगले मैच या सीरीज़ में खेलने की दावेदारी तय होती है; गरीबी या बेरोज़गारी के आँकड़े देश की सरकारों को अपनी नीति निर्धारित करने में मदद करते हैं; एक शिक्षिका आँकड़ों की मदद से अपने पढ़ाने के तरीके व कक्षा के बच्चों के प्रदर्शन के बीच सम्बन्ध देख सकती है और एक परिवार के खर्च से जुड़े आँकड़े उस परिवार का बजट बनाने में काम आते हैं।
ऐसे ही एक वर्कशॉप के दौरान साथियों के साथ गप-शप करते हुए एक आँकड़े से मेरा भी आमना-सामना हो गया। एक साथी बतलाने लगे कि कैसे उनकी जान-पहचान का एक फॉरेस्ट गार्ड, अपने जंगल में होने वाली बाघों की गिनती को हर दफे पाँच ही दर्ज करवाता है। अब इसके पीछे का असली कारण जो भी रहा हो, उस फॉरेस्ट गार्ड ने जो कारण मेरे साथी को बतलाया वो कुछ ऐसा था कि “जब तक कागज़ पर बाघों की संख्या पाँच बनी रहती है, उसकी नौकरी को कोई खतरा नहीं।” पाँच ही क्यों, तो इस पर मेरे साथी का अन्दाज़ा था कि कभी किसी साल में जब बाघों की गिनती असल में की गई होगी तो उनकी संख्या पाँच रही होगी।
आप शायद सोच रहे हों कि बाघों से जुड़े इन आँकड़ों को देखकर क्या किसी वन्य अधिकारी के दिमाग में यह सवाल नहीं उठता होगा कि साल-दर-साल बाघों की संख्या एक ही क्यों बनी हुई है। क्या आँकड़ों में ही कोई गड़बड़ी है या उस जंगल का पारिस्थितिक-तंत्र (इकोसिस्टम) ही कुछ खास है?
मेरे दिमाग में भी ऐसे ही सवाल उठे और साथ ही एक सवाल यह भी कि अगर फॉरेस्ट गार्ड ने बाघों की संख्या का आँकड़ा कुछ इस तरह बतलाया होता कि जंगल में बाघों की औसत संख्या 5 है, तो उस सूरत में हम कैसे सवालों पर विचार कर रहे होते। शायद ये कि क्या बाघों की औसत संख्या बतलाना ही काफी है? आइए इसी सवाल की थोड़ी पड़ताल कर लेते हैं। तालिका-1 में, उदाहरण के तौर पर पिछली पाँच गणनाओं में बाघों की संख्या के तीन अलग-अलग मामले दिखलाए गए हैं।
आप देखेंगे कि इन तीनों ही स्थितियों में बाघों की औसत संख्या तो 5 ही है, लेकिन संख्या में साल-दर-साल होने वाले बदलाव की प्रवृत्ति (nature of change) में ज़मीन-आसमान का अन्तर है। पहले उदाहरण में जहाँ बाघों की संख्या लगातार बढ़ रही है, वहीं दूसरे मामले में यह संख्या लगातार घट रही है। और तीसरे में तो यह पहले बढ़ी और फिर घट गई। साफ तौर पर अगर आप बाघों की संख्या को लेकर चिन्तित हों तो इन तीनों ही स्थितियों में आपकी प्रतिक्रिया अलग-अलग होगी। पर सिर्फ बाघों की औसत संख्या जानने भर से तो इन तीनों उदाहरणों में फर्क कर पाना नामुमकिन होगा
| घटना-क्रम | बाघों की संख्या के पिछले पाँच आँकड़े | बाघों की औसत संख्या | बाघों की संख्या |
| पहला | 2,3,5,7,8 | 5 | लगातार बढ़ रही है |
| दूसरा | 8,7,5,5,2 | 5 | लगातार घट रही है |
| तीसरा | 4,7,5,5,4 | 5 | पहले बढ़ी फिर घटी |
एक अन्य उदाहरण से औसत की अवधारणा की अपर्याप्तता झलकती है। मान लीजिए कि एक ट्रेन किसी स्टेशन से रोज़ाना सुबह साढ़े आठ बजे छूटती है। पैंट्रीकार में आग लगने की वजह से सोमवार के दिन गाड़ी 35 मिनट देर से चली। इसी तरह मंगलवार को 5 मिनट की देरी से, बुधवार को 3 मिनट की देरी से, गुरुवार को 3 मिनट की देरी से व शुक्रवार को 4 मिनट की देरी से चली।
अगर आपको शनिवार सुबह इसी गाड़ी से सफर करना हो और आपके पास बीते पाँच दिनों के आँकड़े हों तो आप किस समय स्टेशन पहुँचना चाहेंगे? इन पाँच दिनों के आँकड़ों का औसत होगा 10 मिनट। निश्चित तौर पर आप इस औसत समय के हिसाब से तो स्टेशन नहीं पहुँचना चाहेंगे, क्योंकि आपको पता है कि यह औसत इतना ज़्यादा इसीलिए है क्योंकि सोमवार को गाड़ी में एक ऐसी घटना घटी जो विशिष्ट है यानी कि अमूमन नहीं होती। और अगर आप इस 10 मिनट के औसत समय के हिसाब से चले तो यह सम्भावना कहीं ज़्यादा है कि जब तक आप स्टेशन पहुँचेंगेे, गाड़ी आपके बिना ही रवाना हो चुकी होगी।
आँकड़ों की समझ बनाते हुए यह बात ध्यान में रखना बहुत ज़रूरी है कि आँकड़े महज़ संख्याएँ नहीं बल्कि किसी खास सन्दर्भ से जुड़े हुए हैं। उन्हें अपने सन्दर्भ से अलग करके नहीं देखा जाना चाहिए। |
असल में जब हम दिए गए आँकड़ों के औसत की बात करते हैं तो हमारा इशारा आँकड़ों से जुड़े एक ऐसे प्रतिनिधिक माप की तरफ होता है जिसे केन्द्र में रखकर हम आँकड़ों की प्रवृत्ति के बारे में एक बेहतर समझ बना सकें। लेकिन जैसा कि हमने बाघों व ट्रेन के उदाहरणों में देखा कि रोज़मर्रा की भाषा में हम जिस औसत की बात करते हैं, वह अपने आप में आँकड़ों की समझ बनाने के लिए काफी नहीं है। इसी कारण से सांख्यिकी में औसत की अवधारणा के कई स्वरूप हैं।
आँकड़ों की केन्द्रीय प्रवृत्ति के माप: माध्य (mean), माध्यक (median))व बहुलक (mode)
सांख्यिकी में आम तौर पर इस्तेमाल किया जाने वाला औसत ही माध्य कहलाता है। आँकड़ों की कुल संख्या से आँकड़ों के कुल जोड़ को भाग देने पर जो राशि हमें मिलेगी वो माध्य कहलाती है। उदाहरण के तौर पर अगर हमारे पास a1,a2,a3... से लेकर an तक कुल n आँकड़े हों तो उनका माध्य होगा:
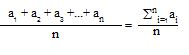
मिनट। साफ ज़ाहिर है कि यह ज़रूरी नहीं कि मिलने वाला औसत दिए हुए आँकड़ों में से ही एक हो। जैसा कि ट्रेन के मामले में सोमवार से लेकर शुक्रवार किसी भी दिन गाड़ी 10 मिनट लेट नहीं रही थी।
माध्यक दिए गए आँकड़ों में से वो अवलोकन होता है जो उन आँकड़ों को दो ऐसे भागों में बाँटता है जिनमें अवलोकनों की संख्या बराबर होती है। साथ ही इन दोनों भागों में से एक के अवलोकन माध्यक के बराबर या कम, व दूसरे भाग के अवलोकन माध्यक के बराबर या उससे ज़्यादा होते हैं। इसे निकालने के लिए हमें दिए गए आँकड़ों को घटते या बढ़ते क्रम में जमाना होता है। ऐसा करने के उपरान्त ठीक बीच वाला अवलोकन माध्यक होता है। अगर अलग-अलग दिनों में ट्रेन के लेट होने के समय को बढ़ते क्रम में जमाएँ तो आँकड़े कुछ ऐसे दिखेंगे - 3, 3, 4, 5, 35। इन आँकड़ों के लिए ठीक बीच वाला अवलोकन होगा 4। इसलिए इन आँकड़ों का माध्यक होगा 4 मिनट। चूँकि इस मामले में आँकड़ों की संख्या विषम है इसलिए हमें बीच का एक ही अवलोकन मिला। अगर आँकड़ों की कुल संख्या एक सम संख्या होती तो उस मामले में हमें मध्य में दो अवलोकन मिलते। ऐसे मामलों में बीच के इन दोनों अवलोकनों का माध्य यानी कि औसत ही माध्यक होता है। अगर आँकड़ों की संख्या विषम हुई तो माध्यक दिए गए आँकड़ों में से ही कोई एक अवलोकन होगा। आँकड़ों की संख्या सम होने की स्थिति में माध्यक दिए गए आँकड़ों में से ही कोई एक अवलोकन हो भी सकता है और नहीं भी।
किसी दिए गए आँकड़े में बहुलक उस अवलोकन के बराबर होता है जो कि सबसे ज़्यादा दफे आया हो, यानी कि ऐसा अवलोकन जिसकी बारम्बारता (frequency) सबसे ज़्यादा हो। ट्रेन वाले उदाहरण में सिर्फ एक ही अवलोकन है जो एक से ज़्यादा बार आया है। ट्रेन 2 दफे 3 मिनट लेट रही है। इसलिए इन आँकड़ों का बहुलक होगा 3 मिनट। साफ तौर पर बहुलक हमेशा ही दिए गए आँकड़ों में से ही कोई एक अवलोकन होगा। ये सम्भव है कि किसी आँकड़े में एक से अधिक अवलोकनों की बारम्बारता बराबर हो या कोई भी अवलोकन ऐसा न हो जो एक से ज़्यादा बार आया हो।
| क्या आप बता सकते हैं कि किस स्थिति में माध्यक दिए गए आँकड़ों में से ही कोई एक अवलोकन होगा और किस स्थिति में नहीं? |
औसत: कब कौन-सा?
औसत की इन तीनों अवधारणाओं को देखने के बाद आप शायद सोच रहे हों कि किस स्थिति में कौन-सा औसत इस्तेमाल किया जाना चाहिए। हालाँकि ये तीनों औसत आँकड़ों के बारे में कुछ-न-कुछ जानकारी तो देते ही हैं। कुछ उदाहरणों की मदद से हम यह समझने का प्रयास करेंगे।
उदाहरण 1: जब आँकड़े गुणात्मक हों
किसी कक्षा में बच्चों से यह पूछा जाए कि उन्हें कौन-सा रंग सबसे ज़्यादा पसन्द है तो जवाब कुछ ऐसे हो सकते हैं - हरा, नीला, काला, गुलाबी, पीला, हरा, सफेद, बैंगनी, नीला इत्यादि। इस मामले में हमारे पास जो आँकड़े हैं वो परिमाण-सम्बन्धी (संख्यात्मक) न होकर गुणात्मक हैं। क्या ऐसी स्थिति में आप माध्य का इस्तेमाल कर सकते हैं? जवाब साफ है, नहीं। माध्य निकालने के लिए दिए गए सभी अवलोकनों को जोड़ना होगा। और जब आँकड़े गुणात्मक हों तो ऐसा करना नामुमकिन होगा। तो क्या गुणात्मक आँकड़ों के लिए माध्यक निकाला जा सकता है? इसका जवाब भी नकारात्मक ही होगा। ज़रा कोशिश करके देखिए आपको खुद ही समझ आ जाएगा कि क्यों। लेकिन गुणात्मक आँकड़ों के लिए बहुलक निकाला जा सकता है क्योंकियह माप बारम्बारता पर निर्भर करता है। रंगों वाले उदाहरण के लिए बहुलक निकालने के लिए हमें देखना होगा कि किस एक रंग को सबसे ज़्यादा बच्चे पसन्द करते हैं।
उदाहरण 2: Outliers की मौजूदगी
सांख्यिकी भाषा में outliers के मायने होते हैं ऐसे अवलोकन जो बाकी सभी अवलोकनों की तुलना में अलग ही दिखाई देते हैं। जैसे कि ट्रेन वाले उदाहरण में सोमवार के दिन दुर्घटना के चलते ट्रेन का 35 मिनट लेट होना। आँकड़ों में मिलने वाले ऐसे अवलोकन चरम मूल्यों (extreme values) को दर्शाते हैं।
ऐसे मामलों में माध्य का इस्तेमाल आँकड़ों की एक गलत तस्वीर पेश करता है लेकिन माध्यक आँकड़ों को बेहतर ढंग से प्रदर्शित करता है, क्योंकि outliers की मौजूदगी इसे खास प्रभावित नहीं करती। एक और तरीका है जो अक्सर ही सांख्यिकीय विश्लेषणों में ऐसे चरम मूल्यों की उपस्थिति होने पर इस्तेमाल किया जाता है। इसमें ऐसे चरम मूल्यों को अलग कर सिर्फ बाकी बचे अवलोकनों का ही इस्तेमाल किया जाता है। उदाहरण के तौर पर ट्रेन के मामले में, जब हम औसत की बात करें तो 35 मिनट के आँकड़े को अपने अवलोकनों में शामिल ही न करें। लेकिन यह तरीका भी सोच-समझकर ही इस्तेमाल में लाया जाना चाहिए।
उदाहरण 3: आँकड़ों का किसी एक तरफ झुकाव
यहाँ एक उदाहरण लेते हैं जो समाज में व्याप्त गैर-बराबरी से जुड़ा हुआ है। नीचे तालिका-2 में एक शिक्षण संस्थान में तरह-तरह के काम करने वाले लोगों की संख्या व उनके वेतनों को तीन समूहों में बाँटकर दिखाया गया है।
संस्थान में काम करने वाले कुल कामगारों की संख्या है:
350 + 500+ 2500 + 3350
इन 3350 लोगों का कुल वेतन होगा:
(350 x 100000) +(500 x 40000) + (2500 x 7000) = 7,25,00,000
यानी कि संस्थान के बजट से प्रतिमाह कुल 7 करोड़ 25 लाख रुपए इन सभी कामगारों के वेतन पर खर्च होते हैं। गौरतलब बात यह है कि मात्र 350 शिक्षकों की वेतन में हिस्सेदारी ही साढ़े तीन करोड़ रुपए है और वहीं 2500 ठेका कामगारों की हिस्सेदारी मात्र 1 करोड़ 75 लाख रुपए की है। साफ तौर पर ये आँकड़े शिक्षकों की तरफ झुके हुए हैं। इन आँकड़ों के लिए माध्य होगा,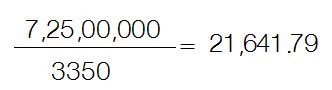
मेरी समझ से इस मामले में बहुलक या माध्यक स्थिति को ज़्यादा बेहतर तरीके से ज़ाहिर करते हैं, क्योंकि बहुलक उस वेतनमान को दर्शा रहा है जो सबसे ज़्यादा कामगारों को मिलता है, साथ ही माध्यक ये बतला रहा है कि कम-से-कम आधे कामगारों को 7000 के बराबर या उससे कम वेतन मिलता है। वहीं माध्य का मान सबसे कम वेतनमान का लगभग तीन गुना है और सबसे ज़्यादा वेतन माध्य का लगभग पाँच गुना है। ऐसे में अगर कोई यह कहे कि संस्थान में काम करने वाले लोगों का मासिकवेतन औसतन 21,641.79 है तो यह संस्थान में वेतन के बँटवारे की सही तस्वीर नहीं होगी।
| शिक्षक | कर्मचारी | ठेका कामगार | |
| संख्या | 350 | 500 | 2500 |
| मासिक वेतन | 1,00,000 | 40,000 | 7,000 |
उदाहरण 4: जब आँकड़ों का झुकाव दोनों तरफ लगभग समान हो
कई दफा किसी आँकड़े के अवलोकन किसी एक केन्द्रीय मान के आसपास होते हैं या माने जाते हैं। इस सूरत में माध्य का इस्तेमाल ज़्यादा होता है। उदाहरण के तौर पर अगर आप एक मेस को लें, जिसमें किसी होस्टल के 400 बच्चे खाना खाते हों। महीने के अन्त में खाने पर हुए कुल खर्च का बच्चों के बीच बँटवारा करने का सबसे बेहतर व आसान तरीका माध्य ही होगा।
कुछ उदाहरण ऐसे भी हो सकते हैं जिनमें माध्य, माध्यक व बहुलक तीनों ही इस्तेमाल न आ सकें, जिसके चलते सांख्यिकी में इन तीनों के अलावा कई अन्य औसत भी इस्तेमाल किए जाते हैं। उनमें से एक उदाहरण क्रिकेट जगत से जुड़ा हुआ है।
बैटिंग औसत
क्या आपने कभी इस बात पर ध्यान दिया कि किसी बल्लेबाज़ के नाम के आगे जो बैटिंग औसत दिखाया जाता है वो न माध्य होता है, न माध्यक और न ही बहुलक। आइए देखते हैं कि वो असल में क्या होता है।
हिन्दुस्तानी क्रिकेट जगत का एक प्रसिद्ध व चर्चित नाम है महेन्द्र सिंह धोनी। आप में से शायद कई लोगों को भी वे अपने खेल व कप्तानी की वजह से पसन्द हों। अगर आज की तारीख में अभी तक के एकदिवसीय मैच खेलने वाले सभी भारतीय बल्लेबाज़ों की उनके बैटिंग औसत के हिसाब से एक लिस्ट बनाई जाए तो धोनी पहले नम्बर पर होंगे और दूसरे नम्बर पर होंगे विराट कोहली। नीचे तालिका-3 में इन दोनों बल्लेबाज़ों का अभी तक का बैटिंग रिकॉर्ड दिया गया है। रिकॉर्ड का यह वही स्वरूप है जो अक्सर ही टीवी या अखबारों में दिख जाता है। वैसे आगे बढ़ने से पहले ज़रा इस बात पर विचार कर लें कि किसी बल्लेबाज़ की क्षमता मापने के लिए सांख्यिकीय माप कैसा होना चाहिए।
| खिलाडी | मैच | परियाँ | नाबाद | कुल रन | सर्वाधिक | बैटिंग ओसत |
| धोनी | 262 | 228 | 66 | 8499 | 183 | 52.46 |
| कोहली | 158 | 150 | 23 | 6357 | 183 | 51.47 |
तालिका में आप देखेंगे कि धोनी ने अब तक कुल 262 एकदिवसीय मैच खेले हैं व कुल 8499 रन बनाए हैं। अब अगर सवाल पूछा जाए कि धोनी ने प्रति मैच औसतन कितने रन बनाए हैं तो आप कुल रनों की संख्या को कुल मैचों की संख्या से विभाजित करके इसका जवाब दे सकते हैं। अगर ऐसा करें तो जो संख्या हमें मिलेगी वो होगी 32.43। क्या यह संख्या सही मायनों में धोनी की एकदिवसीय मैचों में बल्लेबाज़ी के प्रदर्शन को दर्शाती है? थोड़ा सोचने पर आपको इसका जवाब नकारात्मक ही मिलेगा। साफ ज़ाहिर है कि भले ही धोनी ने कुल 262 एकदिवसीय मैच खेले हैं लेकिन इन सभी मैचों में उन्हें बल्लेबाज़ी करने का मौका मिला हो यह ज़रूरी नहीं है। अब जिन मैचों में एक खिलाड़ी ने बल्लेबाजी ही ना की हो तो उन मैचों को उस खिलाड़ी के बैटिंग प्रदर्शन से तो नहीं जोड़ा जाना चाहिए। तालिका में आप देखेंगे कि धोनी ने 262 एकदिवसीय मैचों में कुल 228 पारियाँ ही खेली हैं। और इन्हीं पारियों में उन्होंने 8499 रन बनाए हैं। तो क्या इन रनों की संख्या को कुल पारियों की संख्या से विभाजित करके हम धोनी के एकदिवसीय बल्लेबाज़ी प्रदर्शन को जाँच सकते हैं? अगर ऐसा करें तो जो संख्या हमें मिलेगी वो होगी 37.27। यह संख्या दर्शाती है कि धोनी ने औसतन प्रति पारी कितने रन बनाए और यह एक सूचक हो सकता है किसी खिलाड़ी की रन बना सकने की क्षमता का। कोहली के मामले में यह संख्या होगी 42.38, जो धोनी की प्रति पारी औसत से ज़्यादा है। लेकिन आँकड़ों में हमें यह सूचकांक दिखाई नहीं देता। धोनी का जो बैटिंग औसत तालिका में दिखलाया गया है वो है 52.46 जो प्रति पारी रन औसत 37.27 से कहीं ज़्यादा है।
दरअसल एक खिलाड़ी की बल्लेबाज़ी को सिर्फ उसकी रन बनाने की क्षमता से ही नहीं मापा जाता; एक और पहलू जो उसकी बल्लेबाज़ी को दर्शाता है वो है बल्लेबाज़ी करते हुए उस खिलाड़ी का नाबाद रहना। अब धोनी और कोहली, दोनों का ही एकदिवसीय मैचों में सर्वाधिक स्कोर है 183। लेकिन कोहली इतने रन बनाने के बाद आउट हो गए, वहीं धोनी अन्त तक नाबाद रहे। अगर मैच खत्म ना होता तो हो सकता है कि धोनी और ज़्यादा रन बनाते। लेकिन ऐसा कहना सिर्फ अनुमान ही होगा, वो और कितने रन बनाते ये पता नहीं लगाया जा सकता। इसी सम्भावना व अनुमान के आधार पर ही खिलाड़ियों का बैटिंग औसत निकाला जाता है। बैटिंग औसत निकालते समय केवल उन्हीं पारियों को लिया जाता है जिसमें कोई खिलाड़ी आउट हुआ हो। आप तालिका में देखेंगे कि धोनी अब तक कुल 66 पारियों में नाबाद रहे हैं, यानी कि कुल 162 (228-66) पारियों में वो आउट हुए। अब अगर हम धोनी के बनाए कुल रनों की संख्या को उन पारियों की संख्या से विभाजित करें जिनमें वो आउट हुए तो हमें उनका वही बैटिंग औसत मिलेगा जो तालिका में दिया गया है। ध्यान रहे कि यह एक अनुमानित औसत है क्योंकि इसमें न केवल हकीकत में बनाए गए रनों की संख्या ही शामिल है पर नाबाद रहने की स्थिति में खिलाड़ी द्वारा बनाए जा सकने वाले रनों का भी एक अनुमान शामिल है।
इस लेख में हमने देखा कि केन्द्रीय प्रवृत्ति के विभिन्न मापों से आँकड़ों के बारे में कुछ समझ बनाई जा सकती है। लेकिन इनके अलावा और भी कई माप हैं जिनकी मदद से हम आँकड़ों की पड़ताल और भी बेहतर तरीके से कर सकते हैं। उन पर चर्चा फिर कभी। फिलहाल के लिए एक सवाल से यह लेख खत्म करता हूँ। मुझे याद है जब मैं पहली-दूसरी कक्षा में था तो हम चार दोस्त हुआ करते थे: राजेश, समीर, रामनरेश और मैं। हम चारों में रामनरेश कुछ अलग ही था। वो हम सबसे काफी लम्बा था और उसमें एक बात ऐसी थी जिसे देखकर मैं हमेशा ही अचरज में पड़ जाता था। उसके दोनों हाथों और एक पैर में छ:-छ: उंगलियाँ थीं। अब अगर गणित के शिक्षक हमसे यह सवाल पूछते कि इन्सानी हाथों में औसतन कितनी उंगलियाँ होती हैं, तो चार दोस्तों के आँकड़ों के आधार पर हम क्या जवाब देते: इन्सानी हाथों में औसतन 5.25 उंगलियाँ होती हैं या ?
विवेक मेहता: आई.आई.टी., कानपुर से मेकेनिकल इंजीनियरिंग में पीएच.डी. की है। एकलव्य के विज्ञान शिक्षण कार्यक्रम के साथ फैलोशिप पर हैं।
इससे सम्बन्धित लेख ‘झूठ, सफेद झूठ और आँकड़े’ पढ़िए ‘संदर्भ’ अंक 04 में।